Основные виды уравнений, используемых при различных формах связи между двумя признаками
Решая системы уравнений методом наименьших квадратов, определи параметры уравнения связи:
Параметры а1 и а0 можно определить по формулам:
Параметр а0 - показывает усредненное влияние на результативный признак неучтенных (не выделенных для исследования) факторов. Параметр a1 (коэффициент регрессии) показывает, насколько изменяется в среднем значение результативного признака при увеличении факторного на единицу На основе этого параметра (коэффициента регрессии) вычисляются коэффициенты эластичности, которые показывают изменение результативного признака в % в зависимости от изменения факторного признака на 1 %
Коэффициент эластичности
Эмпирический (перекрестный) коэффициент эластичности
Э - процентные изменения результативного показателя у при изменении х;
Рис.1. Основные этапы проведения корреляционного анализа
|

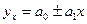 или
или
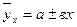 (связь прямолинейная)
(связь прямолинейная)

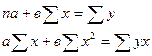
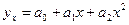 или
у = а + вх+ сх2
(связь криволинейная)
или
у = а + вх+ сх2
(связь криволинейная)
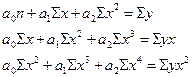

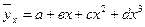 (связь криволинейная)
(связь криволинейная)


 или
или
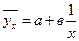 (связь криволинейная)
(связь криволинейная)
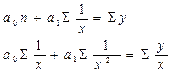
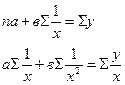
 или
или
 (связь криволинейная)
(связь криволинейная)


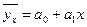


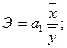
 где
где - прирост фактора х
- прирост фактора х - прирост результативного показателя у
- прирост результативного показателя у