Элементы физики атомного ядра
10.1. Определить массу нейтрального атома хрома 10.2. Объяснить отличие изотопов и изобаров. 10.3. Определить, какую часть массы нейтрального атома 10.4. Определить число протонов и нейтронов, входящих в состав ядер трех изотопов бора: 1) 10.5. Определить число протонов и нейтронов, входящих в состав ядер трех изотопов кислорода: 1) 10.6. Определить, пользуясь таблицей Менделеева, число нейтронов и протонов в атомах платины и урана. 10.7. Определить зарядовые числа ядер, массовые числа и символы ядер, которые получатся, если в ядрах,, нейтроны заменить протонами, а протоны – нейтронами. 10.8. Определить плотность ядерного вещества, выражаемую числом нуклонов в 1 см3, если в ядре с массовым числом А все нуклоны плотно упакованы в пределах его радиуса. Ответ: N = 3/(4π Rd 3) = 8,7.1037 см-3. 10.9. Объяснить, почему плотность ядерного вещества примерно одинакова для всех ядер. 10.10. Определить, что больше – масса атомного ядра или масса свободных нуклонов (протонов и нейтронов), входящих в его состав. 10.11. Определить, какая энергия в электрон-вольтах соответствует дефекту массы Δ m = 3·10-20 мг. Ответ: 16,9 ГэВ. 10.12. Определить энергию связи ядра атома гелия 10.13. Определить удельную энергию связи δ ЕСВ (энергию связи, отнесенную к одному нуклону) для ядер: 1) 10.14. Используя данные задачи 10.13, определить, какая необходима энергия, чтобы разделить ядро 10.15. Определить массу изотопа 10.16. При отрыве нейтрона от ядра гелия 10.17. Энергия связи EСВ ядра, состоящего из трех протонов и четырех нейтронов, равна 39,3 МэВ. Определить массу m нейтрального атома, обладающего этим ядром. Ответ: 1,165.10-26 кг. 10.18. Определить, какую долю кинетической энергии теряет нейтрон при упругом столкновении с покоящимся ядром углерода 10.19. Определить число нуклонов, которые могут находиться в ядре на наинизшем квантовом уровне. Ответ: 4. 10.20. Определить, во сколько раз магнетон Бора (единица магнитного момента электрона) больше ядерного магнетона (единица магнитного момента ядра). Ответ: В 1835 раз. 10.21. Охарактеризовать свойства и особенности сил, действующих между составляющими ядро нуклонами. 10.22. Объяснить принципы построения ядерной и оболочечной моделей ядра. 10.23. Объяснить, почему радиоактивные свойства элементов обусловлены только структурой их ядер. 10.24. Считая постоянную λ радиоактивного распада известной и используя закон радиоактивного распада, вывести выражение для: 1) периода полураспада Т1/2 радиоактивного ядра; 2) среднего времени жизни τ радиоактивного ядра. Ответ: 1) Т1/2 = (ln2)/λ; 2) τ = 1/λ. 10.25. Определить постоянную радиоактивного распада λ для изотопов: 1) тория 10.26. Определить, что (и во сколько раз) продолжительнее – три периода полураспада или два средних времени жизни радиоактивного ядра. 10.27. Определить, во сколько раз начальное количество ядер радиоактивного изотопа уменьшится за три года, если за один год оно уменьшилось в 4 раза. Ответ: В 64 раза. 10.28. Определить, какая часть (%) начального количества ядер радиоактивного изотопа останется нераспавшейся по истечении времени t, равного двум средним временам жизни τ; радиоактивного ядра. Ответ: 13,5 %. 10.29. Определить, какая часть начального количества ядер радиоактивного изотопа распадется за время t, равное двум периодам полураспада T1/2. Ответ: 0,75. 10.30. Определить период полураспада радиоактивного изотопа, если 5/8 начального количества ядер этого изотопа распалось за время t = 849 с. Ответ: 10 мин. 10.31. Период полураспада радиоактивного изотопа актиния 10.32. Постоянная радиоактивного распада изотопа 10.33. Первоначальная масса радиоактивного изотопа иода 10.34. Активность некоторого радиоактивного изотопа в начальный момент времени составляла 100 Бк. Определить активность этого изотопа по истечении промежутка времени, равного половине периода полураспада. Ответ: 70,7 Бк. 10.35. Начальная активность 1 г изотопа радия 10.36. Принимая, что все атомы изотопа магния 10.37. Определить период полураспада T1/2 некоторого радиоактивного изотопа, если его активность за 5 сут уменьшилась в 2,2 раза. Ответ: 4,4 сут. 10.38. Определить удельную активность а (число распадов в 1 с на 1 кг вещества) изотопа 10.39. Объяснить, как изменяется положение химического элемента в таблице Менделеева после α- и β-распадов ядер его атомов. 10.40. Пользуясь таблицей Менделеева и правилами смещения, определить, в какой элемент превращается 10.41. Пользуясь таблицей Менделеева и правилами смещения, определить, в какой элемент превращается 10.42. Ядра радиоактивного изотопа тория 10.43. Определить, сколько β- и α-частиц выбрасывается при превращении ядра таллия 10.44. Радиоактивный изотоп радия 10.45. Записать α; -распад радия 10.46. Покоившееся ядро радона 10.47. Покоившееся ядро полония 10.48. Определить энергию, выделяющуюся в результате реакции 10.49. Записать β - -распад магния 10.50. Известно, что β--активные ядра обладают до распада и после него вполне определенными энергиями, в то же время энергетический спектр β--частиц является непрерывным. Объяснить непрерывность энергетического спектра испускаемых электронов. 10.51. Объяснить, почему существование антинейтрино полностью позволяет объяснить все особенности β--распада. 10.52. Объяснить, почему при α-распаде одинаковых ядер энергии α-частиц одинаковы, а при β--распаде одинаковых ядер энергии электронов различны. 10.53. Применяя понятия квантовой статистики, объяснить, почему невозможно принципиально создать «нейтринный лазер». 10.54. Описать основные процессы, происходящие при взаимодействии γ-излучения с веществом. 10.55. Свободное покоившееся ядро 10.56. Назвать два важных механизма, которыми можно объяснить ослабление потока фотонов с энергией Е = 500 кэВ при его прохождении через вещество. 10.57. Объяснить, где и почему лучше исследовать длинные цепи рождений и распадов частиц высоких энергий – в камере Вильсона или в пузырьковой камере. 10.58. Определить, является ли реакция 10.59. Определить, поглощается или выделяется энергия при ядерной 10.60. Определить, выделяется или поглощается энергия при ядерной реакции 10.61. Определить, выделяется или поглощается энергия при ядерной реакции 10.62. Определить зарядовое число Z и массовое число А частицы, обозначенной буквой х, в символической записи ядерной реакции: 1) 10.63. Записать недостающие обозначения x в следующих ядерных реакциях: 1) 10.64. В ядерной реакции 10.65. Жолио-Кюри облучали алюминий 10.66. Жолио-Кюри облучали магний 10.67. В процессе осуществления реакции γ 10.68. При столкновении позитрона и электрона происходит их аннигиляция, в процессе которой электронно-позитронная пара превращается в два γ-кванта, а энергия пары переходит в энергию фотонов. Определить энергию каждого из возникших фотонов, принимая, что кинетическая энергия электрона и позитрона до их столкновения пренебрежимо мала. Ответ: 0,51 МэВ. 10.69. Записать схему электронного захвата (е -захвата) и объяснить его отличие от β±-распадов. Привести пример электронного захвата. 10.70. Дополнить недостающие обозначения x в следующих ядерных реакциях: 1) 2) 3) 4)
|

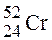 . Ответ: 8,64.10-26 кг.
. Ответ: 8,64.10-26 кг. (m = 19,9272.10-27 кг) составляет масса его электронной оболочки. Ответ: 2,74.10-4.
(m = 19,9272.10-27 кг) составляет масса его электронной оболочки. Ответ: 2,74.10-4.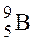 ; 2)
; 2) 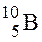 ; 3)
; 3) 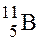 .
. ; 2)
; 2)  ; 3)
; 3)  .
.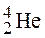 . Масса нейтрального атома гелия равна 6,6467.10-27 кг. Ответ: 28,4 МэВ.
. Масса нейтрального атома гелия равна 6,6467.10-27 кг. Ответ: 28,4 МэВ. ; 2)
; 2) 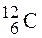 . Массы нейтральных атомов гелия и углерода соответственно равны 6,6467.10-27 и 19,9272.10-27 кг. Ответ: 1) 7,1 МэВ/нуклон; 2) 7,7 МэВ/нуклон.
. Массы нейтральных атомов гелия и углерода соответственно равны 6,6467.10-27 и 19,9272.10-27 кг. Ответ: 1) 7,1 МэВ/нуклон; 2) 7,7 МэВ/нуклон. на три альфа-частицы. Ответ: 7,26 МэВ.
на три альфа-частицы. Ответ: 7,26 МэВ. , если изменение массы при образовании ядра
, если изменение массы при образовании ядра  образуется ядро
образуется ядро  . Определить энергию, которую необходимо для этого затратить. Массы нейтральных атомов
. Определить энергию, которую необходимо для этого затратить. Массы нейтральных атомов  ; 2) урана
; 2) урана  ; 3) иода
; 3) иода 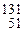 I. Периоды полураспада этих изотопов соответственно равны: 1) 7.103лет; 2) 4,5.109 лет; 3) 8 сут. Ответ: 1) 3,13·10-12 с-1; 2) 4,87·10-18 с-1; 3) 10-6 с-1.
I. Периоды полураспада этих изотопов соответственно равны: 1) 7.103лет; 2) 4,5.109 лет; 3) 8 сут. Ответ: 1) 3,13·10-12 с-1; 2) 4,87·10-18 с-1; 3) 10-6 с-1. составляет 10 сут. Определить время, за которое распадется 1/3 начального количества ядер актиния. Ответ: 5,85 сут.
составляет 10 сут. Определить время, за которое распадется 1/3 начального количества ядер актиния. Ответ: 5,85 сут. равна 10-9 с-1. Определить время, в течение которого распадется 2/5 начального количества ядер этого радиоактивного изотопа. Ответ: 16,2 года.
равна 10-9 с-1. Определить время, в течение которого распадется 2/5 начального количества ядер этого радиоактивного изотопа. Ответ: 16,2 года. (период полураспада Т1/2 = 8 сут) равна 1 г. Определить: 1) начальную активность изотопа; 2) его активность через 3 сут. Ответ: 1) 4,61·1015 Бк; 2) 3,55·1015 Бк.
(период полураспада Т1/2 = 8 сут) равна 1 г. Определить: 1) начальную активность изотопа; 2) его активность через 3 сут. Ответ: 1) 4,61·1015 Бк; 2) 3,55·1015 Бк. равна 1 Ки. Определить период полураспада T1/2 этого изотопа. Ответ: 1582 года.
равна 1 Ки. Определить период полураспада T1/2 этого изотопа. Ответ: 1582 года.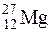 (Т½=10 мин) массой m = 1 мкг радиоактивны, определить: 1) начальную активность А0 этого изотопа; 2) его активность А через 3 сут. Ответ: 1) 4,61 ТБк; 2) 3,55 ТБк.
(Т½=10 мин) массой m = 1 мкг радиоактивны, определить: 1) начальную активность А0 этого изотопа; 2) его активность А через 3 сут. Ответ: 1) 4,61 ТБк; 2) 3,55 ТБк. после шести α- и трех β--распадов, Ответ:
после шести α- и трех β--распадов, Ответ: 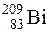 .
.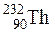 претерпевают последовательно α; -распад, два β--распада и α-распад. Определить конечный продукт деления. Ответ:
претерпевают последовательно α; -распад, два β--распада и α-распад. Определить конечный продукт деления. Ответ:  .
. в ядро свинца
в ядро свинца  . Ответ: Три β-частицы и одна α-частица.
. Ответ: Три β-частицы и одна α-частица. претерпевает четыре α-распада и два β--распада. Определить для конечного ядра: 1) зарядовое число Z; 2) массовое число А. Ответ: 1) 82, 2) 209.
претерпевает четыре α-распада и два β--распада. Определить для конечного ядра: 1) зарядовое число Z; 2) массовое число А. Ответ: 1) 82, 2) 209. испускает α-частицу, имеющую скорость 16 Мм/с. Зная, что масса дочернего ядра составляет 3,62·10-25 кг, определить: 1) импульс α; -частицы; 2) кинетическую энергию α-частицы; З) импульс отдачи дочернего ядра; 4) кинетическую энергию отдачи дочернего ядра. Ответ: 1) 1,07.10-19кг.м/с; 2) 5,35 МэВ; 3) 1,07.10-19 кг.м/с; 4) 9,89 кэВ.
испускает α-частицу, имеющую скорость 16 Мм/с. Зная, что масса дочернего ядра составляет 3,62·10-25 кг, определить: 1) импульс α; -частицы; 2) кинетическую энергию α-частицы; З) импульс отдачи дочернего ядра; 4) кинетическую энергию отдачи дочернего ядра. Ответ: 1) 1,07.10-19кг.м/с; 2) 5,35 МэВ; 3) 1,07.10-19 кг.м/с; 4) 9,89 кэВ.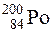 испускает α-частицу с кинетической энергией Тα = 5,77 МэВ. Определить: 1) скорость отдачи дочернего ядра; 2) какую долю кинетической энергии α-частицы составляет энергия отдачи дочернего ядра. Ответ: 1) 339 км/с; 2) 0,02.
испускает α-частицу с кинетической энергией Тα = 5,77 МэВ. Определить: 1) скорость отдачи дочернего ядра; 2) какую долю кинетической энергии α-частицы составляет энергия отдачи дочернего ядра. Ответ: 1) 339 км/с; 2) 0,02.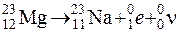 . Массы нейтральных атомов магния и натрия соответственно равны 3,8184.10-26 и 3,8177.10-26 кг. Ответ: Q = 2,91 МэВ.
. Массы нейтральных атомов магния и натрия соответственно равны 3,8184.10-26 и 3,8177.10-26 кг. Ответ: Q = 2,91 МэВ. (m = 317,10953.10-27 кг) с энергией возбуждения E = 129 кэВ перешло в основное состояние, испустив γ-квант. Определить изменение энергии γ-кванта, возникающее в результате отдачи ядра. Ответ: Δε = E2 /(mc2) = 0,047 эВ.
(m = 317,10953.10-27 кг) с энергией возбуждения E = 129 кэВ перешло в основное состояние, испустив γ-квант. Определить изменение энергии γ-кванта, возникающее в результате отдачи ядра. Ответ: Δε = E2 /(mc2) = 0,047 эВ.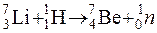 экзотермической или эндотермической. Определить энергию ядерной реакции. Ответ: 1,64 МэВ.
экзотермической или эндотермической. Определить энергию ядерной реакции. Ответ: 1,64 МэВ. . Определить эту энергию. Ответ: 17,6 МэВ.
. Определить эту энергию. Ответ: 17,6 МэВ. . Массы ядер, участвующих в реакции:
. Массы ядер, участвующих в реакции: 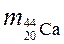 = 7,2992·10-26 кг,
= 7,2992·10-26 кг,  = 1,6736·10-227 кг,
= 1,6736·10-227 кг, 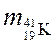 = 6,8021·10-27 кг,
= 6,8021·10-27 кг,  = 6,6467.10-27 кг.
= 6,6467.10-27 кг. . Массы ядер, участвующих в реакции:
. Массы ядер, участвующих в реакции:  = 2,3253·10-26 кг,
= 2,3253·10-26 кг,  = 2,8229.10-26 кг.
= 2,8229.10-26 кг. ; 2)
; 2)  ; 3)
; 3) 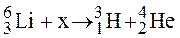 .
.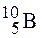 (n, α;) х; 2)
(n, α;) х; 2)  (α;, n) х; 3) x (p, n)
(α;, n) х; 3) x (p, n) 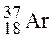 ; 4)
; 4)  (x, p)
(x, p)  ; 5) x (n, α;)
; 5) x (n, α;)  .
. выделяется энергия Δ E = 3,27 МэВ. Определить массу атома
выделяется энергия Δ E = 3,27 МэВ. Определить массу атома  равна 3,34461·10-27 кг. Ответ: 5,00841.10-27кг.
равна 3,34461·10-27 кг. Ответ: 5,00841.10-27кг.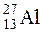 α-частицами, в результате чего испускался нейтрон и образовывалось искусственно-радиоактивное ядро, испытывающее β+-распад.. Записать эту реакцию.
α-частицами, в результате чего испускался нейтрон и образовывалось искусственно-радиоактивное ядро, испытывающее β+-распад.. Записать эту реакцию. α-частицами, в результате чего испускался нейтрон и образовывалось искусственно-радиоактивное ядро, испытывающее β+-распад. Записать данную реакцию.
α-частицами, в результате чего испускался нейтрон и образовывалось искусственно-радиоактивное ядро, испытывающее β+-распад. Записать данную реакцию.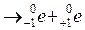 энергия E0 фотона составляла 2,02 МэВ. Определить суммарную кинетическую энергию позитрона и электрона в момент их возникновения. Ответ: 1 МэВ.
энергия E0 фотона составляла 2,02 МэВ. Определить суммарную кинетическую энергию позитрона и электрона в момент их возникновения. Ответ: 1 МэВ.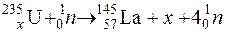 ;
; ;
; ;
; .
.


