Геометрическая сущность картографического изображения.

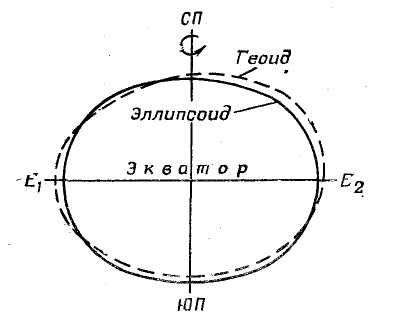
Геометрия картографического изображения связана с пред­ставлением о фигуре Земли — ее геометрической форме и раз­мерах.

Географическое положение точек на земной поверхности опре­деляется, как известно, их координатами. Поэтому математическая задача построения картографического изображения заключается в том, чтобы спроектировать и изобразить шарообразную поверх­ность Земли на плоскости (карте), строго соблюдая при этом од­нозначное соответствие между координатами точек на земной по­верхности и координатами их изображения на карте.

Такое проектирование сопряжено с необходимостью отнесения результатов полевых геодезических измерений при их вычисли­тельной обработке и отображении на картах к определенной, хорошо изученной в геометрическом отношении поверхности, которая наиболее близко подходит по своей форме и размерам к реальной фигуре Земли, но более проста по сравнению с нею.

Под фигурой Земли понимают математическую фигуру, ограниченную поверхностью среднего уровня Мирового океана в спокойном его состоянии, мысленно продолженную под всеми континентами. Эта воображаемая поверхность, перпендикуляр­ная в любой ее точке к направлению отвесной линии (на­правлению силы тяжести), называется основной уровненной поверхностью, а фигура Земли, образованная ею - геоидом.

Геоид, как показали исследования, имеет всюду выпуклую, но асимметричную, сложную и неправильную в геометрическом отно­шении фигуру (рис. 1 и 2), которая, однако, весьма мало отлича­ется от эллипсоида вращения, т. е. правильного геометрического тела, образуемого вращением эллипса вокруг его малой оси. По­этому при геодезических измерениях и составлении карт фигуру Земли и принимают за такой эллипсоид.

Эллипсоид вращения, поверхность которого наиболее близка к поверхности геоида, называют земным эллипсоидом, или земным сфероидом.

 

Рис. 1. Фигура Земли: геоид и земной эллипсоид (сфероид).

 

На картах эту поверхность представляет сетка географических меридианов и параллелей земного эллипсоида. Такая сетка на картах называется картографической сеткой. При состав­лении карты прежде строят картографическую сетку, а затем, пользуясь ею как канвой, наносят по материалам топографической съемки, аэроснимкам и другим материалам изображение всех объектов, которые должны быть показаны на карте.

 

 

 

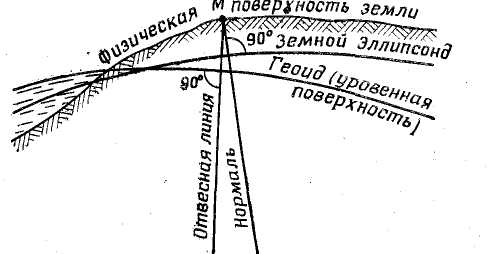
Рис. 2. Физическая и математическая поверхность Земли.

 

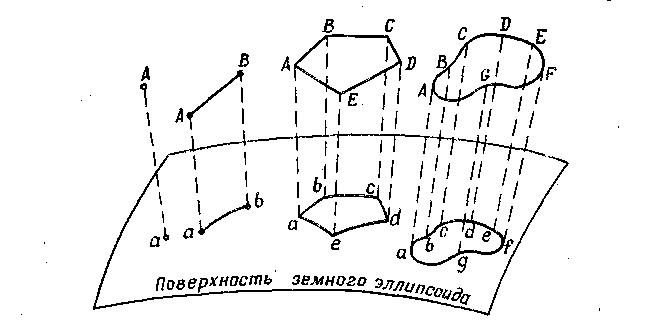
Картографические сетки рассчитываются и строятся на картах по тем или иным математическим формулам, выражающим определенную для данной карты зависимость между географическими координатами точек на поверхности земного эллипсоида и плоскими прямоугольными координатами соответствующих им точек на карте.

Таким образом, нанесение на карту изображения земной по­верхности представляет собой процесс двойного проектирования, включающий одновременно переход от действительных очертаний изображаемых объектов к их горизонтальным проложе­ниям на поверхности земного эллипсоида, т. е. проектирование физической поверхности Земли - на эллипсоид, по нормалям (пер­пендикулярам) к его поверхности (рис. 3), и изображение на пло­скости, т. е. на карте, этих горизонтальных проложений в задан­ном масштабе и по определенным для данной карты математиче­ским правилам.

 

Рис. 3.Горизонтальные проложения точки и различного вида

линий на поверхности земного эллипсоида.

 

Математически определяемый способ построения на плоскости картографической сетки того или иного вида, на основе которой на карте изображают поверхность Земли, называется карто­графической проекцией.