Линейная алгебра
1. Опр. 1 (сумма матриц) Сумма матриц А и В, каждая размерности m x n, есть матрица С размерности m x n с элементами Cij = aij + bij, 2. Утверждение 1 Для любых матриц А, В, С одних и тех же размеров и любых чисел А + В = В + А, (коммутативность) (А + В) + С = (В + С) + А, (ассоциативность)
( 3. Опр. 2 (противоположная матрица) Матрица (−1)А называется противоположной матрице А; обозначается −А. Она обладает свойством А + (− А) = 0. 4. Опр. 3 (разность матриц) Сумма матриц В и −А называется разностью матриц В и А; обозначается В−А 5. Опр. 4 (скалярное произведение строки и столбца)
аb = а1b1 + а2b2 + ….. + аnbn 6. Опр. 5 (произведение матриц) Пусть дана матрица А размеров m x n и матрица В размеров n x p. Матрицы таковы, что число столбцов первой равно числу строк второй. Произведением матриц А и В называется матрица С размеров m x p, столбцы которой составлены из произведений всех строк В (любая строка матрицы С состоит из произведений строки матрицы А, имеющей тот же номер, на все столбцы матрицы В), т.е. элементы матрицы С описываются формулой: Cij = 7. Опр. 6 (перестановочные матрицы) Если какие-нибудь матрицы А и В удовлетворяют соотношению АВ = ВА, то они называются перестановочными. 8. Утверждение 2. Умножение матриц ассоциативно, т.е. если определены произведения АВ и (АВ)С, то определены ВС и А(ВС) и выполнено равенство (АВ)С = А(ВС). 9. Утверждение 3. Умножение матриц дистрибутивно по отношению к сложению, т.е. если имеет смысл выражение А(В + С), то А(В + С) = АВ + АС. Если имеет смысл выражение (А + В)С, то (А + В)С = АС + ВС. 10. Утверждение 4. Если произведение АВ имеет смысл, то
для любого числа 11. Утверждение 5. Умножение матриц дистрибутивно по отношению к сложению, т.е. если имеет смысл выражение А(В + С), то А(В + С) = АВ + АС. Если имеет смысл выражение (А + В)С, то (А + В)С = АКС + АВ. 12. Утверждение 6. Если произведение АВ имеет смысл, то
для любого числа 13. Опр. 7 (высота столбца, длина строки) Число элементов в столбце называется его высотой; число элементов в строке – ее длиной. 14. Опр. 8 (равные столбцы (строки)) Два столбца называются равными, если они одной высоты и равны их элементы, имеющие одинаковые номера. Две строки называются равными, если они одной длины и равны их элементы, имеющие одинаковые номера. 15. Опр. 9 (сумма столбцов) Суммой двух столбцов одной и той же высоты называется столбец, элементы которого равны суммам соответствующих элементов данных столбцов. 16. Опр. 10 (произведение столбца на число) Произведением столбца на число называется столбец, каждый элемент которого равен соответствующему элементу данного столбца, умноженному на это число. 17. Утверждение 7. Для любых столбцов p, q и r одинаковой высоты и любых чисел 2. P + q = q + P – коммутативность сложения. 3. (P + q) + r = P + (q + r) – ассоциативность сложения. 4. 5. ( 18. Опр. 11 (разность столбцов) Разностью P – q столбцов p и q одинаковой высоты называется столбец P + (-1)q. 19. Опр. 12 (линейная комбинация столбцов) Линейной комбинацией столбцов p1, p2, …, pm одинаковой высоты называется столбец q, если при некоторых числах q = 20. Опр. 13 (транспонирование) Матрицу В из n строк и m столбцов, у которой каждая строка является столбцом матрицы А (из m строк и n столбцов) с тем же номером (и следовательно каждый столбец является строкой матрицы А с тем же номером) называют транспонированной матрицей А, а переход от матрицы А к матрице В (или обратно) – транспонированием. Матрицу В обычно обозначают АТ, т.е. В = АТ. Если bij – элемент матрицы В, то bij = aji, где aji – элемент матрицы А.
|

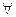 i,j
i,j и
и 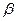 выполнены равенства
выполнены равенства
 Произведением (скалярным) строки а с элементами а i (i = 1, n) и столбца bj (j = 1, n) называется число, равное сумме произведений элементов с одинаковыми номерами (т.е i =j):
Произведением (скалярным) строки а с элементами а i (i = 1, n) и столбца bj (j = 1, n) называется число, равное сумме произведений элементов с одинаковыми номерами (т.е i =j):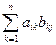 , i- от 1 по m, целые, j - от 1 по p, целые.
, i- от 1 по m, целые, j - от 1 по p, целые. .
.


