РАСПРЕДЕЛЕНИЕ МОЛЕКУЛ ПО СКОРОСТЯМ
(РАСПРЕДЕЛЕНИЕ МАКСВЕЛЛА)
Молекулы газа движутся с самыми разными скоростями, причем, и величина, и направление скорости каждой отдельной молекулы непрерывно меняются из-за соударений. Каждая молекула при н.у. испытывает за секунду порядка 109 столкновений. Хаотичность движения предполагает равную вероятность движения в любом направлении, т.е. равномерное распределение молекул по направлениям. Иначе дело обстоит с численными значениями скоростей. Согласно МКТ, возможные значения u лежат в интервале от нуля до бесконечности и отнюдь не равновероятны. Задача состоит в том, чтобы установить, какая часть от общего числа молекул движется с той или иной скоростью, т.е. найти закон распределения молекул по скоростям. При выводе этого закона Максвелл предполагал, что газ состоит из очень большого числа N одинаковых молекул, находящихся в состоянии беспорядочного теплового движения при постоянной температуре Т. Причём, никакие внешние силы на газ не действуют. Если разбить всю числовую ось скоростей молекул на малые интервалы dυ, то на каждый из них придется некоторое своё число молекул dN(υ) (рис.5): Число dN(υ), очевидно, будет пропорционально общему числу молекул N и ширине интервала dυ. Чтобы определить dN(υ) через N и dυ, необходимо ввести коэффициент пропорциональности, значения которого будут разными для разных интервалов, т.к. т.е. значения скоростей не равновероятны. Т.е. этот коэффициент будет представлять собой некую функцию f(υ). Теперь
Множитель f(υ) характеризует распределение молекул по скоростям и называется функцией распределения. Смысл этой функции в том, что она определяет, какая часть молекул имеет скорости, лежащие в интервале от υ до υ + dυ, т.е. вероятность того, что произвольно взятая молекула в данном газе имеет значение скорости из интервала dυ. Из (21) –
Применяя методы теории вероятностей, Максвелл нашел выражение для функции распределения:
dN/N = f(υ)∙dυ. Очевидно, что площадь под кривой равна единце, т.е.
Значение скорости, на которую приходится максимум функции распределения, называется наиболее вероятной скоростью. Ее можно найти, исследовав функцию f(υ) на экстремум:
Из формулы (25) следует, что при повышении температуры максимум функции f(υ) сместится вправо. Но т.к. площадь под кривой всегда равна единице, то это означает, что при повышении температуры кривая распределения будет растягиваться и понижаться (см. пунктирную линию рис. 6). Из закона распределения скоростей можно получить выражение для средней арифметической скорости молекул:
ОПЫТ ШТЕРНА (1920 Г.)****** Для экспериментальной проверки закона Максвелла немецкий физик Штерн поставил опыт: два коаксиальных жестко скрепленных друг с другом цилиндра вращались с постоянной угловой скоростью ω; вокруг общей оси, вдоль которой была натянута платиновая нить, покрытая серебром. При пропускании тока, нить нагревалась, и серебро испарялось. Атомы серебра разлетались в разные стороны. Некото
|

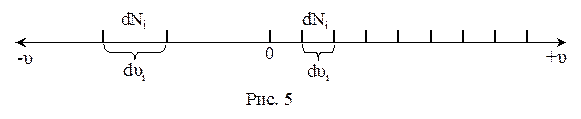 dN(υ) = f(υ)N∙dυ. (21)
dN(υ) = f(υ)N∙dυ. (21) . (22)
. (22) . (23)
. (23) Относительное число молекул, скорости которых лежат в интервале от υ до υ + dυ, как это видно из рисунка, находятся, как площадь заштрихованной полоски:
Относительное число молекул, скорости которых лежат в интервале от υ до υ + dυ, как это видно из рисунка, находятся, как площадь заштрихованной полоски: (24)
(24) (25).
(25). (26).
(26). рые из них вылетали из внутреннего цилиндра через узкую щель и в результате осаждались на внутренней стенке внешнего второго цилиндра. При этом, в зависимости от скорости υ;, отклонение атомов от точки А, будет разным. Чем меньше скорость, тем больше отклонение – зона АВ. Точка А лежит на прямой нить – щель. В эту точку атомы будут попадать, если цилиндры вращаться не будут. Исследование профиля следа АВ (поперечный разрез следа), позволяет судить о распределении атомов серебра по скоростям. Была установлено: профиль следа соответствует форме функции распределения Максвелла.
рые из них вылетали из внутреннего цилиндра через узкую щель и в результате осаждались на внутренней стенке внешнего второго цилиндра. При этом, в зависимости от скорости υ;, отклонение атомов от точки А, будет разным. Чем меньше скорость, тем больше отклонение – зона АВ. Точка А лежит на прямой нить – щель. В эту точку атомы будут попадать, если цилиндры вращаться не будут. Исследование профиля следа АВ (поперечный разрез следа), позволяет судить о распределении атомов серебра по скоростям. Была установлено: профиль следа соответствует форме функции распределения Максвелла.


