В общем случае внутренняя энергия тела представляет собой сумму всех видов энергии, которыми обладают частицы тела. В молекулярной физике под внутренней энергией идеального газа понимают сумму кинетических энергий всех молекул (молекулярное взаимодействие отсутствует).
Полученное нами выражение для средней кинетической энергии молекулы  учитывает только энергию поступательного движения. Однако наряду с поступательным движением возможно также вращение молекул и колебания атомов, входящих в их состав. Понятно, эти виды движения тоже связаны с некоторым запасом энергии. Возникает вопрос, какая доля энергии приходится на тот или другой вид движения? Чтобы ответить на него, введем понятие степени свободы. Под степенями свободы понимают те независимые от других виды движения, которые может совершать данное тело. Например, любое тело обладает тремя степенями свободы поступательного движения: вправо-влево, вперед-назад, вверх-вниз. Соответственно, это приводит к изменению трех координат – X, Y, Z, которые определяют его положение в пространстве. Кроме того, тело может совершать три независимых вращательных движения вокруг трех пространственных осей. Изменение положения тела из-за вращения определяется углами поворота – α, β, γ. Бильярдный шар на плоскости имеет две степени
учитывает только энергию поступательного движения. Однако наряду с поступательным движением возможно также вращение молекул и колебания атомов, входящих в их состав. Понятно, эти виды движения тоже связаны с некоторым запасом энергии. Возникает вопрос, какая доля энергии приходится на тот или другой вид движения? Чтобы ответить на него, введем понятие степени свободы. Под степенями свободы понимают те независимые от других виды движения, которые может совершать данное тело. Например, любое тело обладает тремя степенями свободы поступательного движения: вправо-влево, вперед-назад, вверх-вниз. Соответственно, это приводит к изменению трех координат – X, Y, Z, которые определяют его положение в пространстве. Кроме того, тело может совершать три независимых вращательных движения вокруг трех пространственных осей. Изменение положения тела из-за вращения определяется углами поворота – α, β, γ. Бильярдный шар на плоскости имеет две степени 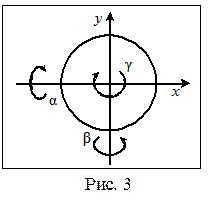 свободы поступательного движения и три степени свободы вращательного движения. Соответственно, положение шара на столе можно задать пятью координатами - x, y и α, β, γ. Таким образом, число степеней свободы любого тела или системы тел равно количеству независимых величин (координат), с помощью которых может быть задано положение макросистемы в пространстве. Исходя из хаотичности молекулярного движения, Максвелл и Больцман пришли к принципу равномерного распределения кинетической энергии молекул по всем степеням свободы. Это значит, что на одну степень свободы поступательного, вращательного или колебательного движения должна приходится одна и та же величина энергии. Т.к. выражение (12) определяет энергию молекулы, которая приходится на три степени свободы поступательного движения, то на одну степень приходится:
свободы поступательного движения и три степени свободы вращательного движения. Соответственно, положение шара на столе можно задать пятью координатами - x, y и α, β, γ. Таким образом, число степеней свободы любого тела или системы тел равно количеству независимых величин (координат), с помощью которых может быть задано положение макросистемы в пространстве. Исходя из хаотичности молекулярного движения, Максвелл и Больцман пришли к принципу равномерного распределения кинетической энергии молекул по всем степеням свободы. Это значит, что на одну степень свободы поступательного, вращательного или колебательного движения должна приходится одна и та же величина энергии. Т.к. выражение (12) определяет энергию молекулы, которая приходится на три степени свободы поступательного движения, то на одну степень приходится:
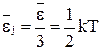 . (16)
. (16)
Тогда кинетическая энергия каждой отдельной молекулы будет определяться формулой:
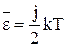 . (17)
. (17)
где j – число степеней свободы молекулы.
Таким образом, проблема внутренней энергии газа сводится к определению числа степеней свободы, которое следует приписать его молекулам. Так как для идеального газа молекулы следует считать материальными точками, то одноатомные газы имеют только три степени свободы поступательного движения (рис.4а). Кинетическая энергия вращательного движения  таких молекул бесконечно мала. В приближении шарообразной молекулы, имеем для момента инерции относительно оси вращения проходящей через центр масс – I = 2mr2/5. Но т.к. r → 0, то I ≈ 0.
таких молекул бесконечно мала. В приближении шарообразной молекулы, имеем для момента инерции относительно оси вращения проходящей через центр масс – I = 2mr2/5. Но т.к. r → 0, то I ≈ 0.
Для двухатомных молекул одну из осей вращения всегда можно совместить с осью молекулы (см. рис.4б). Вращение вокруг этой оси равносильно вращению отдельных атомов вокруг оси через центр масс. Энергия такого движения равна нулю. Поэтому двухатомной молекуле с жесткой связью между атомами следует приписать пять степеней свободы: три поступательного и две вращательного.
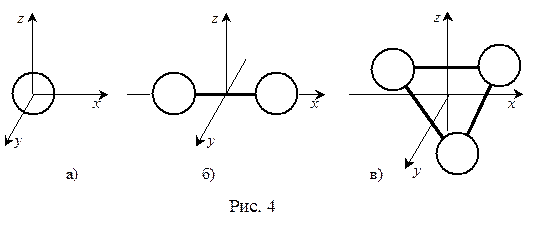 Для молекул с числом атомов три и более (рис.4в), которые связаны между собой жестко, число степеней свободы равно шести.
Для молекул с числом атомов три и более (рис.4в), которые связаны между собой жестко, число степеней свободы равно шести.
Если связь между атомами в молекуле имеет упругий характер, то появляются колебательные степени свободы. Однако учет энергии, связанной с колебательными степенями свободы, как оказалось, довольно сложен, т.к. энергия, которая приходится на одну степень свободы колебательного движения теперь зависит от температуры и частоты колебаний атомов:
 . (18)
. (18)
Опыт показывает, что при небольших температурах энергией колебательного движения можно пренебречь. И мы её в дальнейшем учитывать не будем.
С учётом этого факта внутренняя энергия одного моля идеального газа:
 , (19)
, (19)
где j = 3 для одноатомных; j = 5 для двухатомных; j = 6 для трёхатомных молекул.
Для произвольной массы газа m:
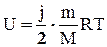 . (20)
. (20)
Эксперимент при низких температурах и невысоких давлениях подтверждает полученные выводы.

 учитывает только энергию поступательного движения. Однако наряду с поступательным движением возможно также вращение молекул и колебания атомов, входящих в их состав. Понятно, эти виды движения тоже связаны с некоторым запасом энергии. Возникает вопрос, какая доля энергии приходится на тот или другой вид движения? Чтобы ответить на него, введем понятие степени свободы. Под степенями свободы понимают те независимые от других виды движения, которые может совершать данное тело. Например, любое тело обладает тремя степенями свободы поступательного движения: вправо-влево, вперед-назад, вверх-вниз. Соответственно, это приводит к изменению трех координат – X, Y, Z, которые определяют его положение в пространстве. Кроме того, тело может совершать три независимых вращательных движения вокруг трех пространственных осей. Изменение положения тела из-за вращения определяется углами поворота – α, β, γ. Бильярдный шар на плоскости имеет две степени
учитывает только энергию поступательного движения. Однако наряду с поступательным движением возможно также вращение молекул и колебания атомов, входящих в их состав. Понятно, эти виды движения тоже связаны с некоторым запасом энергии. Возникает вопрос, какая доля энергии приходится на тот или другой вид движения? Чтобы ответить на него, введем понятие степени свободы. Под степенями свободы понимают те независимые от других виды движения, которые может совершать данное тело. Например, любое тело обладает тремя степенями свободы поступательного движения: вправо-влево, вперед-назад, вверх-вниз. Соответственно, это приводит к изменению трех координат – X, Y, Z, которые определяют его положение в пространстве. Кроме того, тело может совершать три независимых вращательных движения вокруг трех пространственных осей. Изменение положения тела из-за вращения определяется углами поворота – α, β, γ. Бильярдный шар на плоскости имеет две степени  свободы поступательного движения и три степени свободы вращательного движения. Соответственно, положение шара на столе можно задать пятью координатами - x, y и α, β, γ. Таким образом, число степеней свободы любого тела или системы тел равно количеству независимых величин (координат), с помощью которых может быть задано положение макросистемы в пространстве. Исходя из хаотичности молекулярного движения, Максвелл и Больцман пришли к принципу равномерного распределения кинетической энергии молекул по всем степеням свободы. Это значит, что на одну степень свободы поступательного, вращательного или колебательного движения должна приходится одна и та же величина энергии. Т.к. выражение (12) определяет энергию молекулы, которая приходится на три степени свободы поступательного движения, то на одну степень приходится:
свободы поступательного движения и три степени свободы вращательного движения. Соответственно, положение шара на столе можно задать пятью координатами - x, y и α, β, γ. Таким образом, число степеней свободы любого тела или системы тел равно количеству независимых величин (координат), с помощью которых может быть задано положение макросистемы в пространстве. Исходя из хаотичности молекулярного движения, Максвелл и Больцман пришли к принципу равномерного распределения кинетической энергии молекул по всем степеням свободы. Это значит, что на одну степень свободы поступательного, вращательного или колебательного движения должна приходится одна и та же величина энергии. Т.к. выражение (12) определяет энергию молекулы, которая приходится на три степени свободы поступательного движения, то на одну степень приходится: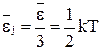 . (16)
. (16)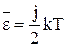 . (17)
. (17) таких молекул бесконечно мала. В приближении шарообразной молекулы, имеем для момента инерции относительно оси вращения проходящей через центр масс – I = 2mr2/5. Но т.к. r → 0, то I ≈ 0.
таких молекул бесконечно мала. В приближении шарообразной молекулы, имеем для момента инерции относительно оси вращения проходящей через центр масс – I = 2mr2/5. Но т.к. r → 0, то I ≈ 0.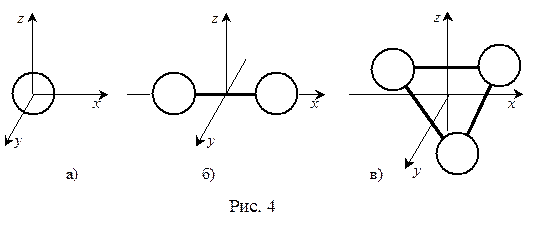 Для молекул с числом атомов три и более (рис.4в), которые связаны между собой жестко, число степеней свободы равно шести.
Для молекул с числом атомов три и более (рис.4в), которые связаны между собой жестко, число степеней свободы равно шести. . (18)
. (18) , (19)
, (19)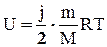 . (20)
. (20)


