Краткая теория
Одной из задач данной работы является определение силы трения между двумя поверхностями - плоскости и скользящего по ней тела. Силой трения F тр называется сила, возникающая при соприкосновении поверхностей двух тел и препятствующая их взаимному перемещению. Она приложена к телам вдоль поверхности их соприкосновения и направлена всегда противоположно относительной скорости перемещения. Трение между поверхностями двух твердых тел при отсутствии какой-либо прослойки (например, смазки между ними) называется сухим. Трение между твердым телом и жидкой или газообразной средой называется вязким. Применительно к сухому трению различают трение скольжения и трение качения. В случае сухого трения сила трения возникает не только при скольжении одной поверхности по другой, но также и при попытках вызвать такое скольжение. В последнем случае она называется силой трения покоя. Положим тяжелый брусок на горизонтальную поверхность стола (рис. 1). В состоянии покоя вес бруска
Если сила Французские физики Г. Амонтон (1663-1705) и Ш. Кулон экспериментально установили, что сила трения
Постоянная μ называется коэффициентом трения и зависит от природы и состояния трущихся поверхностей. Если тело скользит по поверхности другого тела, то μ называют коэффициентом трения скольжения. Если же тела покоятся друг относительно друга, то его называют коэффициентом трения покоя μ0 (при Fтр=F0).
В данном случае на брусок будут действовать три силы: сила тяжести
Из системы уравнений (2) следует, что
Для определения коэффициента трения скольжения запишем уравнение динамики поступательного движения бруска в проекциях на оси OX и OY (рис.3):
Учитывая, что сила трения скольжения равна
где μ – коэффициент трения скольжения. Решая систему уравнений (4) и (5) получаем:
Величину ускорения а можно найти, измерив пройденный бруском путь S и соответствующее время t:
Формула (7) получена при скорости υ = 0, что соответствует условиям эксперимента. Подставляя формулу (7) в выражение (6), получаем:
Рассмотрим скатывающееся тело с наклонной плоскости (рис.4). Оно участвует в двух видах движений: поступательном движении центра масс О и вращательном движении относительно оси, проходящей через центр масс. Скатывание тела без проскальзывания возможно при условии:
где μ – коэффициент трения скольжения тела о наклонную плоскость (коэффициент трения качения пренебрежимо мал); k – коэффициент, входящий в формулу момента инерции тела правильной геометрической формы относительно оси, проходящей через его центр масс (для диска k = 0,5, для шара k = 0,4, для обруча k = 1)
где m – масса тела; R – радиус тела. Поскольку сила трения качения мала, то полная механическая энергия скатывающегося тела постоянна. В начальный момент времени, когда тело покоится на вершине наклонной плоскости на высоте h, его полная механическая энергия равна потенциальной
где L – путь, пройденный центром масс; α – угол наклона плоскости. Кинетическая энергия катящегося тела складывается из кинетической энергии поступательного движения центра масс и вращательного движения относительно оси, проходящей через центр масс:
учитывая, что скорость
|

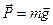 уравновешен силой нормального давления
уравновешен силой нормального давления  , с которой брусок действует стол (P = N).
, с которой брусок действует стол (P = N).
 Приложим затем к бруску горизонтальную силу
Приложим затем к бруску горизонтальную силу  , лежащую в вертикальной плоскости, проходящей через его центр масс, как можно ближе к поверхности стола, чтобы предотвратить опрокидывание бруска, когда он придет в движение. Опыт показывает, что если сила
, лежащую в вертикальной плоскости, проходящей через его центр масс, как можно ближе к поверхности стола, чтобы предотвратить опрокидывание бруска, когда он придет в движение. Опыт показывает, что если сила  (
( ), то брусок не приходит в движение. Отсюда следует сделать вывод, что на брусок со стороны стола действует равная и противоположно направленная сила
), то брусок не приходит в движение. Отсюда следует сделать вывод, что на брусок со стороны стола действует равная и противоположно направленная сила  , уравновешивающая силу
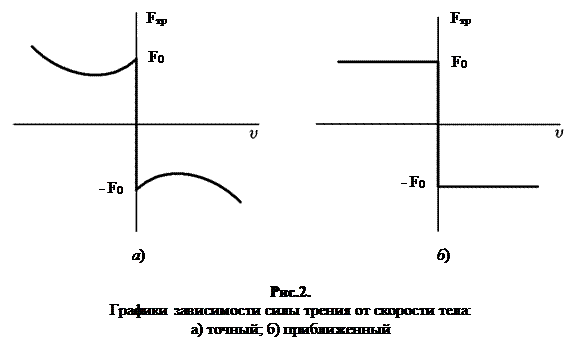
, уравновешивающая силу  , величина которой зависит от скорости скольжения. Характер этой зависимости определяется природой и состоянием трущихся поверхностей. Вид зависимости силы трения от скорости показан на рис.2 (по осям отложены проекции силы трения и скорости на направление, вдоль которых происходит скольжение). Данный график соответствует как случаю трения покоя, так и случаю скольжения. Вертикальным отрезком на графике показано изменение силы трения покоя от нуля до
, величина которой зависит от скорости скольжения. Характер этой зависимости определяется природой и состоянием трущихся поверхностей. Вид зависимости силы трения от скорости показан на рис.2 (по осям отложены проекции силы трения и скорости на направление, вдоль которых происходит скольжение). Данный график соответствует как случаю трения покоя, так и случаю скольжения. Вертикальным отрезком на графике показано изменение силы трения покоя от нуля до 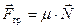 . (1)
. (1)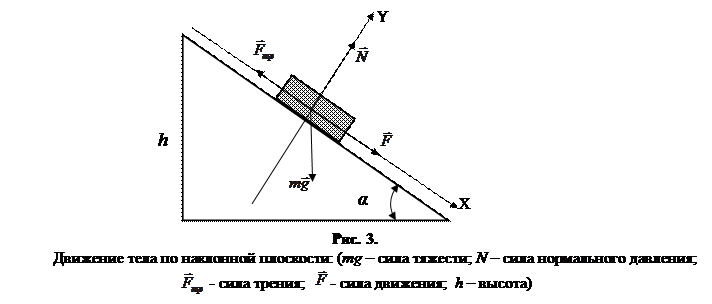
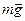 , сила реакции опоры
, сила реакции опоры  . Выберем направление координатной оси X вдоль плоскости вниз, а координатной оси Y перпендикулярно плоскости вверх (рис.3). При отсутствии ускорения равнодействующая всех трех сил равна нулю. Запишем систему уравнений исходя из второго закона Ньютона:
. Выберем направление координатной оси X вдоль плоскости вниз, а координатной оси Y перпендикулярно плоскости вверх (рис.3). При отсутствии ускорения равнодействующая всех трех сил равна нулю. Запишем систему уравнений исходя из второго закона Ньютона: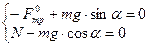 (2)
(2) . Исходя из выражения (1) можно получить
. Исходя из выражения (1) можно получить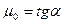 (3).
(3).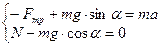 (4)
(4)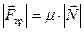 , (5)
, (5)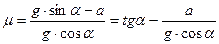 (6)
(6) . (7)
. (7)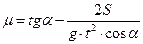 (8)
(8)
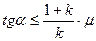 , (9)
, (9)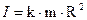 ,
,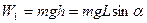 , (10)
, (10) ,
, , где t – время скатывания тела, получим:
, где t – время скатывания тела, получим: (11)
(11)


