Лабораторная работа №3. Программирование условных процессов.
Задание. Составить алгоритм и написать программу для решения следующих задач.
| №
| Условие задачи
| №
| Условие задачи
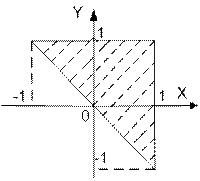
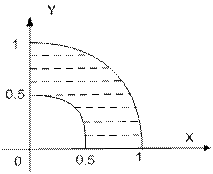
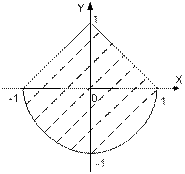
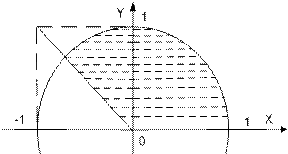
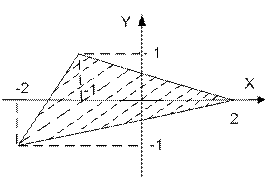
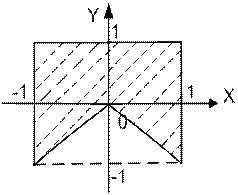
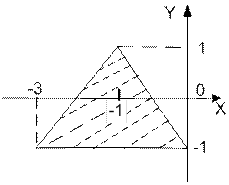
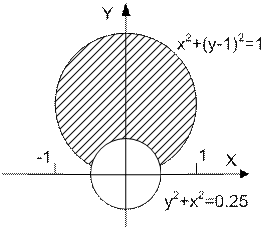
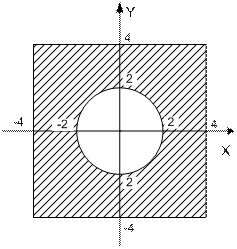
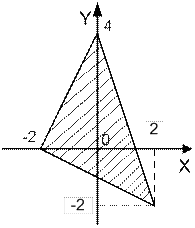
| | Даны вещественные числа x и y. Определить принадлежит ли точка с координатами (x; y) заштрихованной части плоскости.
| |
| 
|
| 
| |
| 
|
| 
| |
| 
|
| 
| |
| 
|
| 
|
| №
| Условие задачи
| №
| Условие задачи
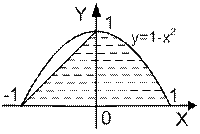
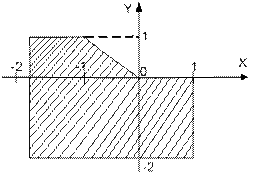
| | Даны вещественные числа x и y. Определить принадлежит ли точка с координатами (x; y) заштрихованной части плоскости.
| |
| 
|
| 
| |
| 
|
| 
| |
| 
|
| 
| |
| 
|
| 
|
| №
| Условие задачи
| №
| Условие задачи
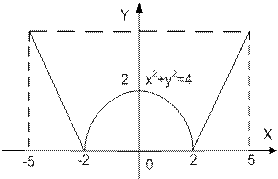
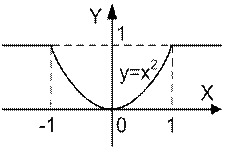
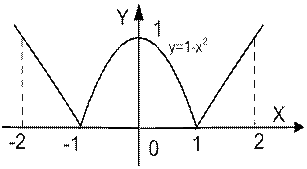
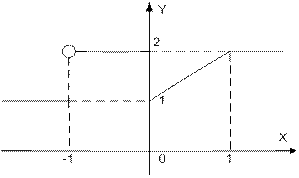
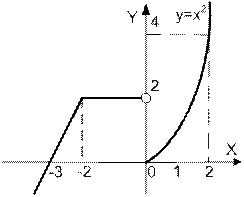
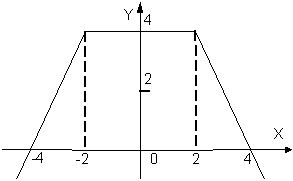
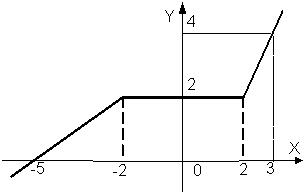
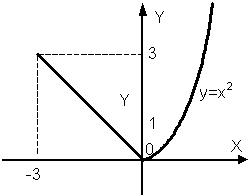
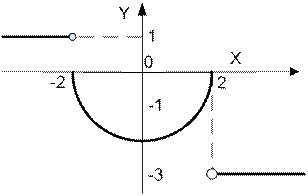
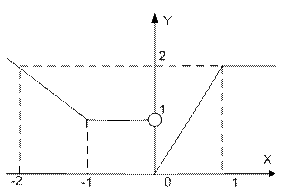
| | Дано вещественное число а. Для функции y = f (x), график которой приведен ниже вычислить f (а).
| |
| 
|
| 
| |
| 
|
| 
| |
| 
|
| 
| |
| 
|
| 
|
| №
| Условие задачи
| №
| Условие задачи
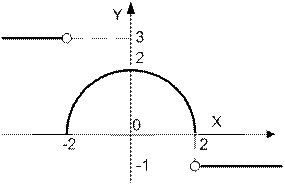
| | Дано вещественное число а. Для функции y = f (x), график которой приведен ниже вычислить f (а).
| |
| 
|
| 
| |
| 
|
| 
| |
| 
|
| 
| № 4. Программирование циклов с известным числом повторений.
Задание. Составить алгоритм и написать программу для решения следующей задачи.
| №
| Условие задачи
| |
| Вычислить значения у, соответствующие каждому значению х (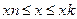 , шаг изменения x равен dx) по формуле , шаг изменения x равен dx) по формуле 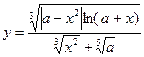 . Вычислить сумму значений у, произведение отрицательных у, количество отрицательных у. Контрольный расчёт провести при a=2.17,xn=-1.5, xk=0.5, dx=0.2. . Вычислить сумму значений у, произведение отрицательных у, количество отрицательных у. Контрольный расчёт провести при a=2.17,xn=-1.5, xk=0.5, dx=0.2.
| |
| Вычислить значения z, соответствующие каждому значению х (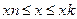 , шаг изменения x равен dx) по формуле , шаг изменения x равен dx) по формуле  . Вычислить сумму значений z, произведение отрицательных z, количество z<0.5. Контрольный расчёт провести при a=2.83, xn=1, xk=2, dx=0.1. . Вычислить сумму значений z, произведение отрицательных z, количество z<0.5. Контрольный расчёт провести при a=2.83, xn=1, xk=2, dx=0.1.
| |
| Вычислить значения t, соответствующие каждому значению х ( , шаг изменения x равен dx) по формуле , шаг изменения x равен dx) по формуле 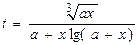 . Вычислить сумму положительных значений t, произведение отрицательных t, количество отрицательных t. Контрольный расчёт провести при a=1.23, xn=-0.5, xk=0.5, dx=0.1. . Вычислить сумму положительных значений t, произведение отрицательных t, количество отрицательных t. Контрольный расчёт провести при a=1.23, xn=-0.5, xk=0.5, dx=0.1.
| |
| Вычислить значения у, соответствующие каждому значению х ( , шаг изменения x равен dx) по формуле , шаг изменения x равен dx) по формуле 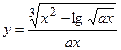 . Вычислить сумму значений у, произведение у. Контрольный расчёт провести при a=2.37, xn=1, xk=3, dx=0.2. . Вычислить сумму значений у, произведение у. Контрольный расчёт провести при a=2.37, xn=1, xk=3, dx=0.2.
| |
| Вычислить значения z, соответствующие каждому значению х ( , шаг изменения x равен dx) по формуле , шаг изменения x равен dx) по формуле 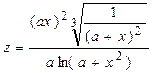 . Вычислить . Вычислить  , сумму значений z, произведение отрицательных z, количество вычислительных z. Контрольный расчёт провести при a=2.62, xn=-3, xk=3, dx=0.6. , сумму значений z, произведение отрицательных z, количество вычислительных z. Контрольный расчёт провести при a=2.62, xn=-3, xk=3, dx=0.6.
| |
| Вычислить значения t, соответствующие каждому значению х (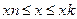 , шаг изменения x равен dx) по формуле , шаг изменения x равен dx) по формуле  . Вычислить сумму значений t³a, произведение t, количество отрицательных t³a. Контрольный расчёт провести при a=3.72, xn=1, xk=3, dx=0.2 . Вычислить сумму значений t³a, произведение t, количество отрицательных t³a. Контрольный расчёт провести при a=3.72, xn=1, xk=3, dx=0.2
| |
| Вычислить значения y, соответствующие каждому значению х (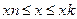 , шаг изменения x равен dx) по формуле , шаг изменения x равен dx) по формуле 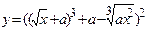 . Вычислить сумму значений y, произведение y, количество вычисленных y. Контрольный расчёт провести при a=2.46, xn=0.5, xk=4.5, dx=0.4. . Вычислить сумму значений y, произведение y, количество вычисленных y. Контрольный расчёт провести при a=2.46, xn=0.5, xk=4.5, dx=0.4.
| | №
| Условие задачи
| |
| Вычислить значения z, соответствующие каждому значению х ( , шаг изменения x равен dx) по формуле , шаг изменения x равен dx) по формуле 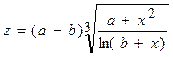 Вычислить сумму значений z, произведение z, количество отрицательных z. Контрольный расчёт провести при a=4.46, b=2.16,xn=-1.5, xk=4.5, dx=0.6. Вычислить сумму значений z, произведение z, количество отрицательных z. Контрольный расчёт провести при a=4.46, b=2.16,xn=-1.5, xk=4.5, dx=0.6.
| |
| Вычислить значения t, соответствующие каждому значению х ( , шаг изменения x равен dx) по формуле , шаг изменения x равен dx) по формуле  . Вычислить сумму значений t, произведение t£200, количество t>200. Контрольный расчёт провести при a=6.13, b=3.42, xn=-2, xk=3, dx=0.5. . Вычислить сумму значений t, произведение t£200, количество t>200. Контрольный расчёт провести при a=6.13, b=3.42, xn=-2, xk=3, dx=0.5.
| |
| Вычислить значения у, соответствующие каждому значению х ( , шаг изменения x равен dx) по формуле , шаг изменения x равен dx) по формуле 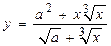 . Вычислить сумму значений y, произведение отрицательных y, количество отрицательных y. Контрольный расчёт провести при a=2.89, xn=-50, xk=50, dx=10. . Вычислить сумму значений y, произведение отрицательных y, количество отрицательных y. Контрольный расчёт провести при a=2.89, xn=-50, xk=50, dx=10.
| |
| Вычислить значения z, соответствующие каждому значению х ( , шаг изменения x равен dx) по формуле , шаг изменения x равен dx) по формуле  . Вычислить сумму значений z>4, произведение z, количество z>4. Контрольный расчёт провести при a=2.94, xn=1.5, xk=5.5, dx=0.4. . Вычислить сумму значений z>4, произведение z, количество z>4. Контрольный расчёт провести при a=2.94, xn=1.5, xk=5.5, dx=0.4.
| |
| Вычислить значения t, соответствующие каждому значению х ( , шаг изменения x равен dx) по формуле , шаг изменения x равен dx) по формуле 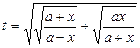 . Вычислить сумму значений t<2, произведение t>2, количество t>2. Контрольный расчёт провести при a=12.94, xn=1, xk=6, dx=0.5. . Вычислить сумму значений t<2, произведение t>2, количество t>2. Контрольный расчёт провести при a=12.94, xn=1, xk=6, dx=0.5.
| |
| Вычислить значения у, соответствующие каждому значению х ( , шаг изменения x равен dx) по формуле , шаг изменения x равен dx) по формуле 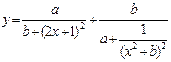 . Определить количество вычисленных y и . Определить количество вычисленных y и 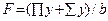 . Контрольный расчёт провести при a=2.91, b=2.41, xn=-4, xk=4, dx=0.8. . Контрольный расчёт провести при a=2.91, b=2.41, xn=-4, xk=4, dx=0.8.
| |
| Вычислить значения z, соответствующие каждому значению х ( , шаг изменения x равен dx) по формуле , шаг изменения x равен dx) по формуле  . Вычислить сумму значений z, произведение z, количество z<0. Контрольный расчёт провести при a=6.13, b=4.28, xn=-3.5, xk=3.5, dx=0.7. . Вычислить сумму значений z, произведение z, количество z<0. Контрольный расчёт провести при a=6.13, b=4.28, xn=-3.5, xk=3.5, dx=0.7.
|
| №
| Условие задачи
| |
| Вычислить значения t, соответствующие каждому значению х ( , шаг изменения x равен dx) по формуле , шаг изменения x равен dx) по формуле 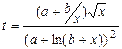 . Вычислить сумму значений t>1, произведение t<1, количество вычисленных t>2. Контрольный расчёт провести при a=2.84, b=4.67, xn=2.5, xk=7.5, dx=0.5. . Вычислить сумму значений t>1, произведение t<1, количество вычисленных t>2. Контрольный расчёт провести при a=2.84, b=4.67, xn=2.5, xk=7.5, dx=0.5.
| |
| Вычислить значения у, соответствующие каждому значению х ( , шаг изменения x равен dx) по формуле , шаг изменения x равен dx) по формуле 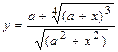 . Вычислить сумму значений y, произведение отрицательных y, количество отрицательных y. Контрольный расчёт провести при a=5.41, xn=-5, xk=5, dx=1. . Вычислить сумму значений y, произведение отрицательных y, количество отрицательных y. Контрольный расчёт провести при a=5.41, xn=-5, xk=5, dx=1.
| |
| Вычислить значения z, соответствующие каждому значению х ( , шаг изменения x равен dx) по формуле , шаг изменения x равен dx) по формуле  . Вычислить сумму значений z£0, произведение z>0, количество вычисленных z. Контрольный расчёт провести при a=4.32, b=8.13, xn=-3, xk=4, dx=0.7. . Вычислить сумму значений z£0, произведение z>0, количество вычисленных z. Контрольный расчёт провести при a=4.32, b=8.13, xn=-3, xk=4, dx=0.7.
| |
| Вычислить значения t, соответствующие каждому значению х ( , шаг изменения x равен dx) по формуле , шаг изменения x равен dx) по формуле  . Вычислить сумму значений t, произведение t<0, количество вычисленных t<0. Контрольный расчёт провести при a=2.56, b=12.7, xn=-2, xk=2, dx=0.4. . Вычислить сумму значений t, произведение t<0, количество вычисленных t<0. Контрольный расчёт провести при a=2.56, b=12.7, xn=-2, xk=2, dx=0.4.
| |
| Вычислить значения у, соответствующие каждому значению х ( , шаг изменения x равен dx) по формуле , шаг изменения x равен dx) по формуле 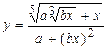 . Вычислить сумму значений y³0, произведение отрицательных y, количество отрицательных y. Контрольный расчёт провести при a=6.42, b=3.17, xn=-3, xk=3, dx=0.6. . Вычислить сумму значений y³0, произведение отрицательных y, количество отрицательных y. Контрольный расчёт провести при a=6.42, b=3.17, xn=-3, xk=3, dx=0.6.
| |
| Вычислить значения z, соответствующие каждому значению х ( , шаг изменения x равен dx) по формуле , шаг изменения x равен dx) по формуле 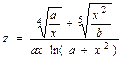 . Вычислить сумму вычисленных значений z, произведение и количество. Контрольный расчёт провести при a=3.53, b=6.12, xn=1, xk=3, dx=0.2 . Вычислить сумму вычисленных значений z, произведение и количество. Контрольный расчёт провести при a=3.53, b=6.12, xn=1, xk=3, dx=0.2
| |
| Вычислить значения t, соответствующие каждому значению х ( , шаг изменения x равен dx) по формуле , шаг изменения x равен dx) по формуле 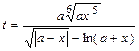 . Определить количество вычисленных t и . Определить количество вычисленных t и 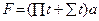 . Контрольный расчёт провести при a=3.42, xn=-2, xk=2, dx=0.4. . Контрольный расчёт провести при a=3.42, xn=-2, xk=2, dx=0.4.
|
| №
| Условие задачи
| |
| Вычислить значения у, соответствующие каждому значению х ( , шаг изменения x равен dx) по формуле , шаг изменения x равен dx) по формуле 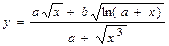 . Определить . Определить 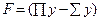 . Контрольный расчёт провести при a=2.47, b=4.82, xn=2.5, xk=5.5, dx=0.3. . Контрольный расчёт провести при a=2.47, b=4.82, xn=2.5, xk=5.5, dx=0.3.
| |
| Вычислить значения z, соответствующие каждому значению х ( , шаг изменения x равен dx) по формуле , шаг изменения x равен dx) по формуле 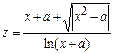 . Вычислить сумму вычисленных значений z<a, произведение z и количество z<a. Контрольный расчёт провести при a=3.42, xn=-2, xk=3, dx=0.5. . Вычислить сумму вычисленных значений z<a, произведение z и количество z<a. Контрольный расчёт провести при a=3.42, xn=-2, xk=3, dx=0.5.
| |
| Вычислить значения t, соответствующие каждому значению х ( , шаг изменения x равен dx) по формуле , шаг изменения x равен dx) по формуле 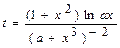 . Вычислить сумму значений t³500, произведение t<500, количество вычисленных t³500. Контрольный расчёт провести при a=2.5, xn=1.5, xk=5.5, dx=0.4. . Вычислить сумму значений t³500, произведение t<500, количество вычисленных t³500. Контрольный расчёт провести при a=2.5, xn=1.5, xk=5.5, dx=0.4.
| |
| Вычислить значения у, соответствующие каждому значению х ( , шаг изменения x равен dx) по формуле , шаг изменения x равен dx) по формуле 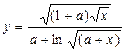 . Вычислить сумму значений y<a, произведение и количество y³a. Контрольный расчёт провести при a=2.57, xn=2, xk=5, dx=0.3. . Вычислить сумму значений y<a, произведение и количество y³a. Контрольный расчёт провести при a=2.57, xn=2, xk=5, dx=0.3.
| № 5. Программирование циклов с неизвестным числом повторений.
Составить алгоритм и написать программу для решения следующей задачи.
| №
| Условие задачи
| |
| Дано: а =4; dа=-0.5. S вычислять по формуле: S = 2.79ln(a3+a+1). Считать S до тех пор, пока выражение под знаком логарифма больше 1. Определить k – количество вычисленных S. Вывести на экран a, S, k.
| |
| Дано: q =3; dq=-0.2. F вычислять по формуле: 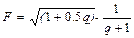 . Считать до тех пор, пока подкоренное выражение больше 0. Определить k – количество вычисленных F. Вывести на экран q, F, k. . Считать до тех пор, пока подкоренное выражение больше 0. Определить k – количество вычисленных F. Вывести на экран q, F, k.
| |
| Дано: x=2; dx=-0.2. Z вычислять по формуле: 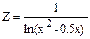 . Считать Z до тех пор, пока выражение под знаком логарифма больше 0. Определить k – количество вычисленных Z. Вывести на экран k, Z, x. . Считать Z до тех пор, пока выражение под знаком логарифма больше 0. Определить k – количество вычисленных Z. Вывести на экран k, Z, x.
| |
| Дано: а = 1.2; x =1;dx= 0.5. Z вычислять по формуле: 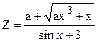 . Считать Z до тех пор, пока подкоренное выражение меньше 250. Определить k – количество вычисленных Z. Вывести на экран x, Z, k. . Считать Z до тех пор, пока подкоренное выражение меньше 250. Определить k – количество вычисленных Z. Вывести на экран x, Z, k.
| |
| Дано: а =5; dа=-0.5. Z вычислять по формуле: 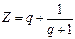 , где q = a2 – a. Считать до тех пор, пока q > 0. Определить k – количество вычисленных Z. Вывести на экран a, q, Z, k. , где q = a2 – a. Считать до тех пор, пока q > 0. Определить k – количество вычисленных Z. Вывести на экран a, q, Z, k.
| |
| Дано: а=3.7; x=2; dx=0.2. Z вычислять по формуле: Z=0.5cos(x)+ln(a/x3 +1/x). Считать Z до тех пор, пока выражение под знаком логарифма больше 0.3. Определить k – количество вычисленных Z. Вывести на экран x, Z, k.
| |
| Дано: x=1; dx=0.5. Z вычислять по формуле: Z = q(cos(3x)+sin(5x)), где q = ex-1 + x. Считать до тех пор, пока q < 400. Определить k – количество вычисленных Z. Вывести на экран x, q, Z, k.
| |
| Дано: x=1; dx=0.5. Z вычислять по формуле:  , где , где 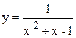 . Считать Z до тех пор, пока y > 0.02. Определить k – количество вычисленных Z. Вывести на экран x, y, Z, k. . Считать Z до тех пор, пока y > 0.02. Определить k – количество вычисленных Z. Вывести на экран x, y, Z, k.
| |
| Дано: x=-1.5;dx=0.5. Z вычислять по формуле:  . Считать Z до тех пор, пока выражение под знаком логарифма больше 0.05. Определить k – количество вычисленных Z. Вывести на экран x, Z, k. . Считать Z до тех пор, пока выражение под знаком логарифма больше 0.05. Определить k – количество вычисленных Z. Вывести на экран x, Z, k.
| |
| Дано: b=1; db=-0.2. Z вычислять по формуле: 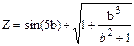 . Считать Z до тех пор, пока подкоренное выражение больше 0. Определить k – количество вычисленных Z. Вывести на экран b, Z, k. . Считать Z до тех пор, пока подкоренное выражение больше 0. Определить k – количество вычисленных Z. Вывести на экран b, Z, k.
| |
| Дано: x=2; dx=-0.2. Z вычислять по формуле: 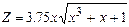 . Считать Z до тех пор, пока подкоренное выражение больше 0. Определить k – количество вычисленных Z. Вывести на экран x, Z, k. . Считать Z до тех пор, пока подкоренное выражение больше 0. Определить k – количество вычисленных Z. Вывести на экран x, Z, k.
| | №
| Условие задачи
| |
| Дано: а=5; dа=-0.5. Z вычислять по формуле: Z = ln(1+0.8a)cos(a). Считать Z до тех пор, пока выражение под знаком логарифма больше 0. Определить k – количество вычисленных Z. Вывести на экран a, Z, k.
| |
| Дано: x=3; dx =-0.2. Z вычислять по формуле: 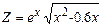 . Считать Z до тех пор, пока подкоренное выражение больше 0. Определить k – количество вычисленных Z. Вывести на экран x, Z, k. . Считать Z до тех пор, пока подкоренное выражение больше 0. Определить k – количество вычисленных Z. Вывести на экран x, Z, k.
| |
| Дано: x=4; dx =-0.3. Z вычислять по формуле: Z = ln(5x-5)sin(x). Считать Z до тех пор, пока выражение под знаком логарифма больше 0. Определить k - количество вычисленных Z. Вывести на экран x, Z, k.
| |
| Дано: x =1; dx=0.2 Z вычислять по формуле:  , где , где 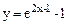 .Считать Z до тех пор, пока y < 150. Определить k - количество вычисленных Z. Вывести на экран x, y, Z, k. .Считать Z до тех пор, пока y < 150. Определить k - количество вычисленных Z. Вывести на экран x, y, Z, k.
| |
| Дано: а=2; dа=0.5. Z вычислять по формуле: 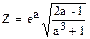 . Считать Z до тех пор, пока подкоренное выражение больше 0.03. Определить k - количество вычисленных Z. Вывести на экран a, Z, k. . Считать Z до тех пор, пока подкоренное выражение больше 0.03. Определить k - количество вычисленных Z. Вывести на экран a, Z, k.
| |
| Дано: b=3; db= -0.3. Z вычислять по формуле: 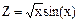 , где x = 0.3b3+b. Считать Z до тех пор, пока x>0. Определить k - количество вычисленных Z. Вывести на экран b, x, Z, k. , где x = 0.3b3+b. Считать Z до тех пор, пока x>0. Определить k - количество вычисленных Z. Вывести на экран b, x, Z, k.
| |
| Дано: x=2; dx=0.4. Z вычислять по формуле: 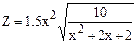 . Считать Z до тех пор, пока подкоренное выражение больше или равно 0.2. Определить k - количество вычисленных Z. Вывести на экран x, Z, k. . Считать Z до тех пор, пока подкоренное выражение больше или равно 0.2. Определить k - количество вычисленных Z. Вывести на экран x, Z, k.
| |
| Дано: с =3.2; а=1; dа=0.3. Z вычислять по формуле: 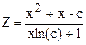 , где , где 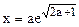 . Считать Z до тех пор, пока x < 100. Определить k - количество вычисленных Z. Вывести на экран a, x, Z, k. . Считать Z до тех пор, пока x < 100. Определить k - количество вычисленных Z. Вывести на экран a, x, Z, k.
| |
| Дано: x=3; dx=-0.4. Z вычислять по формуле: 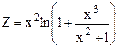 . Считать Z до тех пор, пока выражение под знаком логарифма больше 0. Определить k - количество вычисленных Z. Вывести на экран x, Z, k. . Считать Z до тех пор, пока выражение под знаком логарифма больше 0. Определить k - количество вычисленных Z. Вывести на экран x, Z, k.
| |
| Дано: x =0; dx=0.5. Z вычислять по формуле: 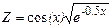 . Считать Z до тех пор, пока подкоренное выражение больше 0.1. Определить k - количество вычисленных Z. Вывести на экран x, Z, k. . Считать Z до тех пор, пока подкоренное выражение больше 0.1. Определить k - количество вычисленных Z. Вывести на экран x, Z, k.
| |
| Дано: а=1; dа=0.4. Z вычислять по формуле: 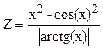 , где x=(a2 +2a+3)-1. Считать Z до тех пор, пока x > 0.02. Определить k - кол-во вычисленных Z. Вывести на экран a, x, Z, k. , где x=(a2 +2a+3)-1. Считать Z до тех пор, пока x > 0.02. Определить k - кол-во вычисленных Z. Вывести на экран a, x, Z, k.
|
| №
| Условие задачи
| |
| Дано: x =6; dx=-0.5. Z вычислять по формуле: Z = cos(x)ln(x2-0.5x). Считать Z до тех пор, пока выражение под знаком логарифма больше 0. Определить k - количество вычисленных Z. Вывести на экран x, Z, k.
| |
| Дано: x=5;.dx=-0.4. Z вычислять по формуле: 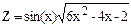 . Считать Z до тех пор, пока выражение под знаком корня больше 0.02. Определить k - количество вычисленных Z. Вывести на экран x,Z,k . Считать Z до тех пор, пока выражение под знаком корня больше 0.02. Определить k - количество вычисленных Z. Вывести на экран x,Z,k
| |
| Дано: b=1; db=0.2. Z вычислять по формуле: 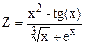 , где , где  . Считать Z до тех пор, пока x > 0.1. Определить k - количество вычисленных Z. Вывести на экран b, x, Z, k . Считать Z до тех пор, пока x > 0.1. Определить k - количество вычисленных Z. Вывести на экран b, x, Z, k
|

Шрифт зодчего Шрифт зодчего состоит из прописных (заглавных), строчных букв и цифр...
|

Картограммы и картодиаграммы Картограммы и картодиаграммы применяются для изображения географической характеристики изучаемых явлений...
|

Практические расчеты на срез и смятие При изучении темы обратите внимание на основные расчетные предпосылки и условности расчета...
|

Функция спроса населения на данный товар Функция спроса населения на данный товар: Qd=7-Р. Функция предложения: Qs= -5+2Р,где...
|
Огоньки» в основной период В основной период смены могут проводиться три вида «огоньков»: «огонек-анализ», тематический «огонек» и «конфликтный» огонек...
Упражнение Джеффа. Это список вопросов или утверждений, отвечая на которые участник может раскрыть свой внутренний мир перед другими участниками и узнать о других участниках больше...
Влияние первой русской революции 1905-1907 гг. на Казахстан. Революция в России (1905-1907 гг.), дала первый толчок политическому пробуждению трудящихся Казахстана, развитию национально-освободительного рабочего движения против гнета. В Казахстане, находившемся далеко от политических центров Российской империи...
|
Эндоскопическая диагностика язвенной болезни желудка, гастрита, опухоли Хронический гастрит - понятие клинико-анатомическое, характеризующееся определенными патоморфологическими изменениями слизистой оболочки желудка - неспецифическим воспалительным процессом...
Признаки классификации безопасности Можно выделить следующие признаки классификации безопасности.
1. По признаку масштабности принято различать следующие относительно самостоятельные геополитические уровни и виды безопасности.
1.1. Международная безопасность (глобальная и...
Прием и регистрация больных Пути госпитализации больных в стационар могут быть различны. В центральное приемное отделение больные могут быть доставлены:
1) машиной скорой медицинской помощи в случае возникновения острого или обострения хронического заболевания...
|
|































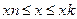 , шаг изменения x равен dx) по формуле
, шаг изменения x равен dx) по формуле 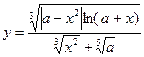 . Вычислить сумму значений у, произведение отрицательных у, количество отрицательных у. Контрольный расчёт провести при a=2.17,xn=-1.5, xk=0.5, dx=0.2.
. Вычислить сумму значений у, произведение отрицательных у, количество отрицательных у. Контрольный расчёт провести при a=2.17,xn=-1.5, xk=0.5, dx=0.2.
 . Вычислить сумму значений z, произведение отрицательных z, количество z<0.5. Контрольный расчёт провести при a=2.83, xn=1, xk=2, dx=0.1.
. Вычислить сумму значений z, произведение отрицательных z, количество z<0.5. Контрольный расчёт провести при a=2.83, xn=1, xk=2, dx=0.1.
 , шаг изменения x равен dx) по формуле
, шаг изменения x равен dx) по формуле 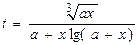 . Вычислить сумму положительных значений t, произведение отрицательных t, количество отрицательных t. Контрольный расчёт провести при a=1.23, xn=-0.5, xk=0.5, dx=0.1.
. Вычислить сумму положительных значений t, произведение отрицательных t, количество отрицательных t. Контрольный расчёт провести при a=1.23, xn=-0.5, xk=0.5, dx=0.1.
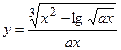 . Вычислить сумму значений у, произведение у. Контрольный расчёт провести при a=2.37, xn=1, xk=3, dx=0.2.
. Вычислить сумму значений у, произведение у. Контрольный расчёт провести при a=2.37, xn=1, xk=3, dx=0.2.
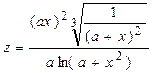 . Вычислить
. Вычислить  , сумму значений z, произведение отрицательных z, количество вычислительных z. Контрольный расчёт провести при a=2.62, xn=-3, xk=3, dx=0.6.
, сумму значений z, произведение отрицательных z, количество вычислительных z. Контрольный расчёт провести при a=2.62, xn=-3, xk=3, dx=0.6.
 . Вычислить сумму значений t³a, произведение t, количество отрицательных t³a. Контрольный расчёт провести при a=3.72, xn=1, xk=3, dx=0.2
. Вычислить сумму значений t³a, произведение t, количество отрицательных t³a. Контрольный расчёт провести при a=3.72, xn=1, xk=3, dx=0.2
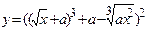 . Вычислить сумму значений y, произведение y, количество вычисленных y. Контрольный расчёт провести при a=2.46, xn=0.5, xk=4.5, dx=0.4.
. Вычислить сумму значений y, произведение y, количество вычисленных y. Контрольный расчёт провести при a=2.46, xn=0.5, xk=4.5, dx=0.4.
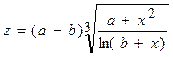 Вычислить сумму значений z, произведение z, количество отрицательных z. Контрольный расчёт провести при a=4.46, b=2.16,xn=-1.5, xk=4.5, dx=0.6.
Вычислить сумму значений z, произведение z, количество отрицательных z. Контрольный расчёт провести при a=4.46, b=2.16,xn=-1.5, xk=4.5, dx=0.6.
 . Вычислить сумму значений t, произведение t£200, количество t>200. Контрольный расчёт провести при a=6.13, b=3.42, xn=-2, xk=3, dx=0.5.
. Вычислить сумму значений t, произведение t£200, количество t>200. Контрольный расчёт провести при a=6.13, b=3.42, xn=-2, xk=3, dx=0.5.
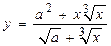 . Вычислить сумму значений y, произведение отрицательных y, количество отрицательных y. Контрольный расчёт провести при a=2.89, xn=-50, xk=50, dx=10.
. Вычислить сумму значений y, произведение отрицательных y, количество отрицательных y. Контрольный расчёт провести при a=2.89, xn=-50, xk=50, dx=10.
 . Вычислить сумму значений z>4, произведение z, количество z>4. Контрольный расчёт провести при a=2.94, xn=1.5, xk=5.5, dx=0.4.
. Вычислить сумму значений z>4, произведение z, количество z>4. Контрольный расчёт провести при a=2.94, xn=1.5, xk=5.5, dx=0.4.
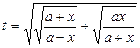 . Вычислить сумму значений t<2, произведение t>2, количество t>2. Контрольный расчёт провести при a=12.94, xn=1, xk=6, dx=0.5.
. Вычислить сумму значений t<2, произведение t>2, количество t>2. Контрольный расчёт провести при a=12.94, xn=1, xk=6, dx=0.5.
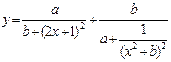 . Определить количество вычисленных y и
. Определить количество вычисленных y и 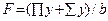 . Контрольный расчёт провести при a=2.91, b=2.41, xn=-4, xk=4, dx=0.8.
. Контрольный расчёт провести при a=2.91, b=2.41, xn=-4, xk=4, dx=0.8.
 . Вычислить сумму значений z, произведение z, количество z<0. Контрольный расчёт провести при a=6.13, b=4.28, xn=-3.5, xk=3.5, dx=0.7.
. Вычислить сумму значений z, произведение z, количество z<0. Контрольный расчёт провести при a=6.13, b=4.28, xn=-3.5, xk=3.5, dx=0.7.
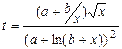 . Вычислить сумму значений t>1, произведение t<1, количество вычисленных t>2. Контрольный расчёт провести при a=2.84, b=4.67, xn=2.5, xk=7.5, dx=0.5.
. Вычислить сумму значений t>1, произведение t<1, количество вычисленных t>2. Контрольный расчёт провести при a=2.84, b=4.67, xn=2.5, xk=7.5, dx=0.5.
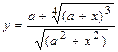 . Вычислить сумму значений y, произведение отрицательных y, количество отрицательных y. Контрольный расчёт провести при a=5.41, xn=-5, xk=5, dx=1.
. Вычислить сумму значений y, произведение отрицательных y, количество отрицательных y. Контрольный расчёт провести при a=5.41, xn=-5, xk=5, dx=1.
 . Вычислить сумму значений z£0, произведение z>0, количество вычисленных z. Контрольный расчёт провести при a=4.32, b=8.13, xn=-3, xk=4, dx=0.7.
. Вычислить сумму значений z£0, произведение z>0, количество вычисленных z. Контрольный расчёт провести при a=4.32, b=8.13, xn=-3, xk=4, dx=0.7.
 . Вычислить сумму значений t, произведение t<0, количество вычисленных t<0. Контрольный расчёт провести при a=2.56, b=12.7, xn=-2, xk=2, dx=0.4.
. Вычислить сумму значений t, произведение t<0, количество вычисленных t<0. Контрольный расчёт провести при a=2.56, b=12.7, xn=-2, xk=2, dx=0.4.
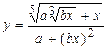 . Вычислить сумму значений y³0, произведение отрицательных y, количество отрицательных y. Контрольный расчёт провести при a=6.42, b=3.17, xn=-3, xk=3, dx=0.6.
. Вычислить сумму значений y³0, произведение отрицательных y, количество отрицательных y. Контрольный расчёт провести при a=6.42, b=3.17, xn=-3, xk=3, dx=0.6.
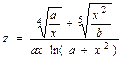 . Вычислить сумму вычисленных значений z, произведение и количество. Контрольный расчёт провести при a=3.53, b=6.12, xn=1, xk=3, dx=0.2
. Вычислить сумму вычисленных значений z, произведение и количество. Контрольный расчёт провести при a=3.53, b=6.12, xn=1, xk=3, dx=0.2
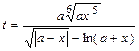 . Определить количество вычисленных t и
. Определить количество вычисленных t и 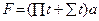 . Контрольный расчёт провести при a=3.42, xn=-2, xk=2, dx=0.4.
. Контрольный расчёт провести при a=3.42, xn=-2, xk=2, dx=0.4.
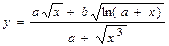 . Определить
. Определить 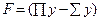 . Контрольный расчёт провести при a=2.47, b=4.82, xn=2.5, xk=5.5, dx=0.3.
. Контрольный расчёт провести при a=2.47, b=4.82, xn=2.5, xk=5.5, dx=0.3.
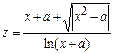 . Вычислить сумму вычисленных значений z<a, произведение z и количество z<a. Контрольный расчёт провести при a=3.42, xn=-2, xk=3, dx=0.5.
. Вычислить сумму вычисленных значений z<a, произведение z и количество z<a. Контрольный расчёт провести при a=3.42, xn=-2, xk=3, dx=0.5.
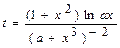 . Вычислить сумму значений t³500, произведение t<500, количество вычисленных t³500. Контрольный расчёт провести при a=2.5, xn=1.5, xk=5.5, dx=0.4.
. Вычислить сумму значений t³500, произведение t<500, количество вычисленных t³500. Контрольный расчёт провести при a=2.5, xn=1.5, xk=5.5, dx=0.4.
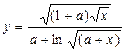 . Вычислить сумму значений y<a, произведение и количество y³a. Контрольный расчёт провести при a=2.57, xn=2, xk=5, dx=0.3.
. Вычислить сумму значений y<a, произведение и количество y³a. Контрольный расчёт провести при a=2.57, xn=2, xk=5, dx=0.3.
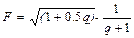 . Считать до тех пор, пока подкоренное выражение больше 0. Определить k – количество вычисленных F. Вывести на экран q, F, k.
. Считать до тех пор, пока подкоренное выражение больше 0. Определить k – количество вычисленных F. Вывести на экран q, F, k.
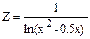 . Считать Z до тех пор, пока выражение под знаком логарифма больше 0. Определить k – количество вычисленных Z. Вывести на экран k, Z, x.
. Считать Z до тех пор, пока выражение под знаком логарифма больше 0. Определить k – количество вычисленных Z. Вывести на экран k, Z, x.
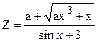 . Считать Z до тех пор, пока подкоренное выражение меньше 250. Определить k – количество вычисленных Z. Вывести на экран x, Z, k.
. Считать Z до тех пор, пока подкоренное выражение меньше 250. Определить k – количество вычисленных Z. Вывести на экран x, Z, k.
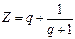 , где q = a2 – a. Считать до тех пор, пока q > 0. Определить k – количество вычисленных Z. Вывести на экран a, q, Z, k.
, где q = a2 – a. Считать до тех пор, пока q > 0. Определить k – количество вычисленных Z. Вывести на экран a, q, Z, k.
 , где
, где 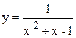 . Считать Z до тех пор, пока y > 0.02. Определить k – количество вычисленных Z. Вывести на экран x, y, Z, k.
. Считать Z до тех пор, пока y > 0.02. Определить k – количество вычисленных Z. Вывести на экран x, y, Z, k.
 . Считать Z до тех пор, пока выражение под знаком логарифма больше 0.05. Определить k – количество вычисленных Z. Вывести на экран x, Z, k.
. Считать Z до тех пор, пока выражение под знаком логарифма больше 0.05. Определить k – количество вычисленных Z. Вывести на экран x, Z, k.
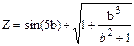 . Считать Z до тех пор, пока подкоренное выражение больше 0. Определить k – количество вычисленных Z. Вывести на экран b, Z, k.
. Считать Z до тех пор, пока подкоренное выражение больше 0. Определить k – количество вычисленных Z. Вывести на экран b, Z, k.
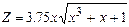 . Считать Z до тех пор, пока подкоренное выражение больше 0. Определить k – количество вычисленных Z. Вывести на экран x, Z, k.
. Считать Z до тех пор, пока подкоренное выражение больше 0. Определить k – количество вычисленных Z. Вывести на экран x, Z, k.
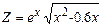 . Считать Z до тех пор, пока подкоренное выражение больше 0. Определить k – количество вычисленных Z. Вывести на экран x, Z, k.
. Считать Z до тех пор, пока подкоренное выражение больше 0. Определить k – количество вычисленных Z. Вывести на экран x, Z, k.
 , где
, где 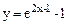 .Считать Z до тех пор, пока y < 150. Определить k - количество вычисленных Z. Вывести на экран x, y, Z, k.
.Считать Z до тех пор, пока y < 150. Определить k - количество вычисленных Z. Вывести на экран x, y, Z, k.
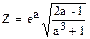 . Считать Z до тех пор, пока подкоренное выражение больше 0.03. Определить k - количество вычисленных Z. Вывести на экран a, Z, k.
. Считать Z до тех пор, пока подкоренное выражение больше 0.03. Определить k - количество вычисленных Z. Вывести на экран a, Z, k.
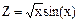 , где x = 0.3b3+b. Считать Z до тех пор, пока x>0. Определить k - количество вычисленных Z. Вывести на экран b, x, Z, k.
, где x = 0.3b3+b. Считать Z до тех пор, пока x>0. Определить k - количество вычисленных Z. Вывести на экран b, x, Z, k.
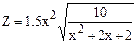 . Считать Z до тех пор, пока подкоренное выражение больше или равно 0.2. Определить k - количество вычисленных Z. Вывести на экран x, Z, k.
. Считать Z до тех пор, пока подкоренное выражение больше или равно 0.2. Определить k - количество вычисленных Z. Вывести на экран x, Z, k.
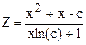 , где
, где 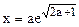 . Считать Z до тех пор, пока x < 100. Определить k - количество вычисленных Z. Вывести на экран a, x, Z, k.
. Считать Z до тех пор, пока x < 100. Определить k - количество вычисленных Z. Вывести на экран a, x, Z, k.
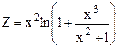 . Считать Z до тех пор, пока выражение под знаком логарифма больше 0. Определить k - количество вычисленных Z. Вывести на экран x, Z, k.
. Считать Z до тех пор, пока выражение под знаком логарифма больше 0. Определить k - количество вычисленных Z. Вывести на экран x, Z, k.
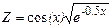 . Считать Z до тех пор, пока подкоренное выражение больше 0.1. Определить k - количество вычисленных Z. Вывести на экран x, Z, k.
. Считать Z до тех пор, пока подкоренное выражение больше 0.1. Определить k - количество вычисленных Z. Вывести на экран x, Z, k.
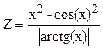 , где x=(a2 +2a+3)-1. Считать Z до тех пор, пока x > 0.02. Определить k - кол-во вычисленных Z. Вывести на экран a, x, Z, k.
, где x=(a2 +2a+3)-1. Считать Z до тех пор, пока x > 0.02. Определить k - кол-во вычисленных Z. Вывести на экран a, x, Z, k.
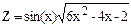 . Считать Z до тех пор, пока выражение под знаком корня больше 0.02. Определить k - количество вычисленных Z. Вывести на экран x,Z,k
. Считать Z до тех пор, пока выражение под знаком корня больше 0.02. Определить k - количество вычисленных Z. Вывести на экран x,Z,k
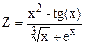 , где
, где  . Считать Z до тех пор, пока x > 0.1. Определить k - количество вычисленных Z. Вывести на экран b, x, Z, k
. Считать Z до тех пор, пока x > 0.1. Определить k - количество вычисленных Z. Вывести на экран b, x, Z, k



