Характеристика модели экспоненциального роста. Объясните обязательные условия этой модели.
В основе модели экспоненциального роста лежит простое и естественное предположение о том, что скорость роста популяции пропорциональна численности этой популяции где xt - численность популяции в момент времени t, а r - так называемая удельная скорость роста численности, которую можно представить как разность удельной рождаемости (birth rate) b и удельной смертности (death rate) d. Это уравнение описывает базовое состояние популяции при отсутствии внешних влияний, аналогичное, в некотором смысле, состоянию покоя или равномерного прямолинейного движения в первом законе Ньютона (Турчин, 2001). Уравнение (1) можно легко проинтегрировать методом разделения переменных. Для этого представим его в виде и проинтегрируем правую часть от 0 до t, а левую - от x 0 (численность популяции в момент t =0) до xt (численность популяции в момент t). Получаем что дает т.е. действительно, уравнение (1) описывает динамику экспоненциально растущей популяции. Рассмотрим совместную динамику численностей xt и yt двух экспоненциально растущих популяций, характеризующихся удельными скоростями роста rx и ry. Она описывается системой двух дифференциальных уравнений Мы будем рассматривать систему (3) как простейшую модель конкуренции двух популяций X и Y, различающихся своими удельными скоростями роста. Конечно, говорить о конкуренции в данном случае можно лишь с большой натяжкой, поскольку обе популяции неограниченно увеличивают свою численность независимо друг от друга. Тем не менее можно задаться вопросом о том, как изменяются со временем относительные численности популяций из которых следует, что если rx > ry, то Проиллюстрируем полученный результат графически. Можно воспользоваться для этого, например, пакетом программ STATISTICA. Надо создать (в режиме File -New) новый пустой файл данных из 1001 строк и 3 столбцов с именами t, ksi, eta, после чего написать (в режиме Analysis - STATISTCA BASIC) и выполнить (кнопкой Execute) следующую программу:
Sequential; rx:=0.04; ry:=0.05; x0:=99; y0:=1; t:=caseno-1; ksi:=1/(1+(y0/x0)*exp((ry-rx)*t)); eta:=1/((x0/y0)*exp((rx-ry)*t)+1);
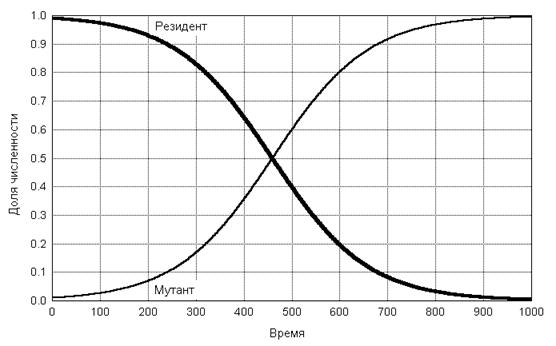
После этого в режиме "Graphs - Stats 2D Graphs - Scatterplots - Graph Type Multiple - Fit Off" можно построить графики зависимости переменных ksi и eta (откладываются по оси ординат) от времени t (откладывается по оси абсцисс). На рис. 1 приведен соответствующий график. Мы видим, что действительно, для rx = 0.04 и ry = 0.05 (что соответствует примерно 4- и 5-процентному приросту численностей популяций X и Y за единицу времени) доля численности популяции X в конечном итоге приближается к нулю, а доля популяции Y - к единице.
Рис. 1. Динамика долей численности t и t популяций резидента X и мутанта Y при экспоненциальном росте для случая rx = 0.04, ry = 0.05 и x 0 = 99 и y 0= 1. Полученные результаты представляет интерес не только с точки зрения сравнительного анализа динамики численности двух экспоненциально растущих популяций. Они позволяют сделать довольно содержательные выводы относительно возможного направления эволюции в рассматриваемой ситуации. Рассмотрим их с этой точки зрения. Удельные скорости роста rx и ry, которые можно рассматривать как фенотипические характеристики популяций X и Y, которые при постоянных внешних условиях определяются генотипами этих популяций. Любое изменение генотипа можно рассматривать, в конечном итоге, с точки зрения его влияния на удельную скорость роста новой популяции, соответствующей измененному генотипу. Пусть популяция X является исходной (резидентной), а популяция Y возникла в результате мутации (в этом случае естественно, для наглядности, задать начальную численность x 0 гораздо больше y 0, как это, в частности, сделано в примере, показанном на рис. 1). Из проведенного выше анализа следует, что если ry > rx, то доля популяции, порожденной мутантом, в суммарной численности двух популяций будет стремиться к 1, т.е. мутации, увеличивающие удельную скорость роста имеют селективное преимущество при естественном отборе. Таким образом, в ситуации неограниченного экспоненциального роста удельная скорость роста популяции r (параметр Мальтуса) является естественной мерой эволюционной (дарвиновской) приспособленности. В результате естественного отбора субпопуляции (кланы) с более высокой удельной скоростью роста неизбежно увеличивают свою относительную численность, что дает основания интерпретировать эволюцию в данной постановке задачи как процесс максимизации r. Конечно, в более реалистичных постановках задачи следует вводить дополнительные условия, предотвращающие неограниченное возрастание критерия приспособленности в процессе его эволюционной оптимизации, однако на данном уровне анализа это обстоятельство не имеет принципиального значения.
|


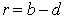
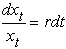



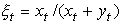 и
и 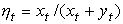 . Мы можем, учитывая (2), получить следующие выражения для
. Мы можем, учитывая (2), получить следующие выражения для  и
и 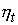
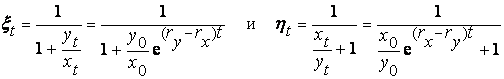
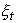 стремится к 1, а
стремится к 1, а 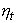 к нулю, а если rx < ry то, наоборот,
к нулю, а если rx < ry то, наоборот, 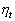 к 1.
к 1.