Розв’язання. Будь-який борг складається з початкової та кінцевої величини

Будь-який борг складається з початкової та кінцевої величини. Початкова сума боргу відрізняється від кінцевої величини на величину відсоткових грошей, сплачених за користування кредитом протягом строку дії фінансової угоди. Кінцева сума боргу складається з початкової суми боргу і приєднаних до неї нагромаджених відсоткових грошей, тому її ще називають нарощеною сумою боргу.

 

Якщо відсотки нараховуються від початкової суми боргу за ставкою один раз у кінці року, то за кожний рік сума боргу зростатиме на величину (P₀i), де P₀ – початкова сума боргу, i – сума відсотків. У кінці першого року борг становитиме (P₀+P₀i), другого – (P₀+2P₀i); третього - (P₀+3P₀i); через n років нарощена сума боргу дорівнюватиме (P₀+nP₀i), тобто S=P₀(1+in), де P₀ni – сума відсоткових грошей, нарахованих за n років.

 

Отже суму простих відсотків, нарахованих за n років, визначають за формулою:

 

,

де P₀ – початкова сума боргу,

n – строк позики в роках або кількість періодів нарахувань,

i – ставка відсотків.

 

Нарощену суму боргу з простими відсотками розраховують за формулою:

 

 

Відповідно умов задачі нарощена сума боргу з простими відсотками буде дорівнювати:

 

Видно, що сума боргу з нарахованими простими відсотками змінюється за арифметичною прогресією

 

P₀; P₀+P₀i; P₀+2P₀i; P₀+3P₀i; P₀+4P₀i.

 

Відобразимо процес нарощення простих відсотків на графіку.

 

 

 

 

Формула нарощування простих відсотків і графік показують, що сума відсоткових грошей прямо пропорційно залежить від початкової суми боргу, ставки податків і строку боргу.

Отже, при короткострокових фінансових операціях використовують прості відсотки, які визначають, виходячи із початкової суми боргу. В довгострокових фінансово-кредитних операціях відсотки не виплачують відразу після їх нарахування, а приєднують до суми боргу. В таких випадках процес нарахування відсотків ґрунтується на складних відсотках. Тобто за базу нарахування нових відсоткових грошей використовують кожного разу іншу (більшу) суму – змінювана база нарахування відсотків (величина боргу разом із нарахованими за попередні періоди часу відсотками). Ставку відсотків, яку при цьому застосовують, називають складною.

Складний – це відсоток, для нарахування якого за базу беруть нарощену суму попереднього періоду. В зв’язку з цим процес нарощення початкової суми відбувається з прискоренням, яке викликане тим, що в кожному часовому проміжку нараховані відсотки приєднують до суми, яка слугувала базою їх нарахування. Такий процес називають капіталізацією відсотків.

Для обчислення нарощеної суми боргу за складними відсотками використовують формулу:

,

де P₀ – початкова сума боргу,

i – складна річна ставка відсотків,

n – строк нарахування відсотків,

(1+i)ⁿ – множник нарощених складних відсотків.

Визначимо суму боргу, яку поверне боржник через 4 роки:

.

Порівняння формул нарощення суми боргу за простими та складними відсотками дало можливість встановити такі закономірності:

якщо n > 1, то (1+in) < (1+i)ⁿ,

якщо n = 1, то (1+in) = (1+i)ⁿ,

якщо n < 1, то (1+in) > (1+i)ⁿ.

6,553Р₀/3,4Р₀ = 1,9275≈1,93

 

Відповідь: нарощена сума боргу за складними відсотками дорівнює 6,5536P₀, за простими відсотками – 3,4P_0. Це в 1,93 рази більше, ніж за простими відсотками (6,5536/3,4=1,93).

ЗАДАЧА 5.
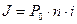
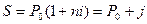
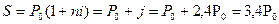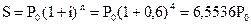