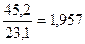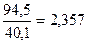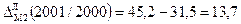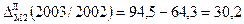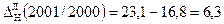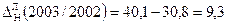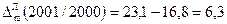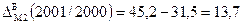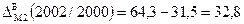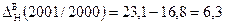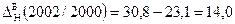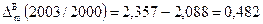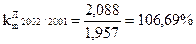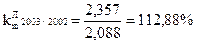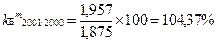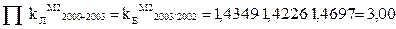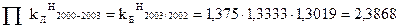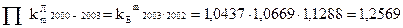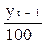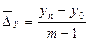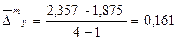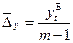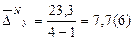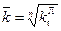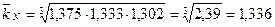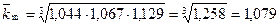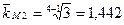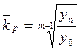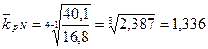Розв’язання. В сучасних умовах пропозиція грошей визначається, як правило, величиною готівкової емісії

В сучасних умовах пропозиція грошей визначається, як правило, величиною готівкової емісії. Розмір цієї емісії залежить не тільки від розмірів грошової бази, а й від можливості банківської системи до збільшення коштів, що до неї надходять. Цю здатність банківської системи до збільшення (скорочення) грошової маси в обігу в результаті скорочення (зростання) банківських резервів характеризує грошовий мультиплікатор.

Грошовий мультиплікатор – коефіцієнт, що характеризує зв’язок між збільшенням (скороченням) надлишкових резервів банківської системи і сумою нових кредитних вкладень, яку вона може створити.Він розраховується за формулою:

,

де m – грошовий мультиплікатор;

М – грошова маса (грошовий агрегат М2);

Н – грошова база.

Грошова база – це сума готівки в обігу (М0), готівки в касах банків та резервів комерційних банків на кореспондентських рахунках у Центральному банку.

Грошовий мультиплікатор використовують для здійснення контролю за змінами грошової маси в обігу та аналізу можливості комерційних банків розширювати обсяги кредитних вкладень в економіку.

Виконаємо розрахунок грошового мультиплікатора за кожний рік.

m₂₀₀₀ =

m₂₀₀₁ =

m₂₀₀₂ =

m₂₀₀₃ =

Отже, спостерігається щорічне збільшення грошового мультиплікатора (з 1,875 у 2000 році до 2,357 в 2003 році).

 

Розрахуємо темпи зростання грошової маси, грошової бази та грошового мультиплікатора. Темп зростання k_t розраховується як відношення рівнів ряду і може бути виражений за допомогою коефіцієнтів або у відсотках:

Для розрахунку темпів зростання маємо інтервальний ряд динаміки з рівними інтервалами (2000-2003 роки). Проаналізуємо ряд динаміки для грошової маси М2, грошової бази та грошового мультиплікатора.

 

Грошові агрегати – це зобов’язання банківської системи не фінансовим секторам: готівка, депозити до запитання, строкові депозити та заощадження. Згідно законодавства України передбачено чотири грошові агрегати (М0-М3). Грошовий агрегат М2 включає:

· грошовий агрегат М1 (національна готівка (агрегат М0), поточні депозити та розрахункові рахунки);

· строкові та нагромаджувальні депозити;

· валютні кошти.

 

Проаналізуємо грошову базу як самостійний компонент грошової маси. Грошова база – це сума готівки в обігу (М0), готівки в касах банків та резервів комерційних банків на кореспондентських рахунках у Центральному банку.

 

Абсолютний приріст (зниження) ∆ − це різниця рівнів динамічного ряду:

ланцюгові: ∆_t = y_t - y_t-1,

базисні: ∆_t = y_t - y_о.

 

Абсолютні прирости для грошової маси (М2) за 2000-2003рр. ланцюгові:

Абсолютні прирости для грошової бази за 2000-2003рр. ланцюгові:

Абсолютні прирости для грошового мультиплікатора за 2000-2003рр. ланцюгові:

 

Абсолютні прирости для грошової маси (М2) за 2000-2003рр. базисні:

Абсолютні прирости для грошової бази за 2000-2003рр. базисні:

Абсолютні прирости для грошового мультиплікатора за 2000-2003рр. базисні:

Сума ланцюгових абсолютних приростів дорівнює кінцевому базисному:

- для грошової маси М2

- для грошової бази Н

- для грошового мультиплікатора

 

Коли характеризують послідовну зміну досліджуваного явища період за періодом, тобто кожен наступний період порівнюють з кожним попереднім, то такі індекси називають ланцюговими.

Ланцюгові коефіцієнти або темпи зростання розрахуємо, використовуючи наступну формулу:

 

Для грошової маси М2:

 

 

Для грошової бази:

 

 

 

 

 

Для грошового мультиплікатора m:

Визначаємо базові коефіцієнти зростання, використовуючи наступну формулу:

 

 

Для грошової маси (М2):

Для грошової бази:

Для грошового мультиплікатора:

Між ланцюговими і базисними темпами зростання існує певний зв’язок. Так, послідовне перемноження ланцюгових темпів дає базисний індекс відповідного періоду:

- для грошової маси М2

- для грошової бази Н

- для грошового мультиплікатора m

 

Абсолютне значення 1% приросту розраховується як відношення абсолютного приросту і темпу приросту. Алгебраїчно це відношення дорівнює 0,01 рівня, прийнятого за базу порівняння:

Для грошової маси М2:

А%_{М2 2001/2000}=31,5/100=0,315

А%_{М2 2002/2001}=45,2/100=0,452

А%_{М2 2003/2002}=64,3/100=0,643

 

Для грошової бази N:

А%_{N 2001/2000}=16,8/100=0,168

А%_{N 2002/2001}=23,1/100=0,231

А%_{N 2003/2002}=30,8/100=0,308

 

Для грошового мультиплікатора m:

А%_{m 2001/2000}=1,875/100=0,001875

А%_{m 2002/2001}=1,957/100=0,001957

А%_{m 2003/2002}=2,088/100=0,002088

 

Абсолютними характеристиками інтенсивності динаміки являються середній абсолютний приріст та середньорічний темп зростання.

Середній абсолютний приріст може розраховуватись:

- як середня арифметична проста із ланцюгових абсолютних приростів;

- на основі абсолютних рівнів динамічного ряду;

- на основі нагромаджених базисних абсолютних приростів.

 

Визначимо середній абсолютний приріст як середню арифметичну просту із ланцюгових абсолютних приростів:

де n – число ланцюгових абсолютних приростів.

Для грошової маси М2:

Для грошової бази N:

Для грошового мультиплікатора m:

Визначимо середній абсолютний приріст на основі абсолютних рівнів динамічного ряду:

Для грошової маси М2:

Для грошової бази N:

Для грошового мультиплікатора m:

 

Визначимо середній абсолютний приріст на основі нагромаджених базисних абсолютних приростів:

Для грошової маси М2:

Для грошової бази N:

Для грошового мультиплікатора m:

 

Середньорічний темп зростання можемо розрахувати:

- на основі ланцюгових темпів росту:

Для грошової маси М2:

Для грошової бази N:

Для грошового мультиплікатора m:

- на основі базисних темпів росту:

Для грошової маси М2:

Для грошової бази N:

Для грошового мультиплікатора m:

- на абсолютних рівнях динамічного ряду:

Для грошової маси М2:

Для грошової бази N:

Для грошового мультиплікатора m:

 

Отже, середній річний темп зростання грошової маси М2, грошової бази N, грошового мультиплікатора m за 2000-2004 року склав 1,442, 1,336 та 1,079 відповідно.

Це означає, що середньорічний темп приросту грошової маси М2 склав 44,2%, грошової бази N – 33,6%, грошового мультиплікатора – 7,9%.

 

Результати розрахунків темпів зростання занесемо у таблицю.