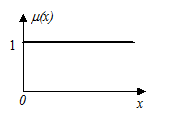
Нечеткие числа (НЧ) L-R типа. Типовые термы, определяемые с помощью НЧ L-R типа.
Нечёткие числа – это нечёткие переменные, определённые на числовой оси. Иначе говоря, нечёткое число определяется как нечёткое множество А на множестве действительных чисел R с функцией принадлежности
Нечёткое число А нормально, если
Чёткое подмножество SA SA = {x/mA(x) > 0}. Нечёткое число А положительно, если А1 - положительное НЧ А2 - отрицательное НЧ
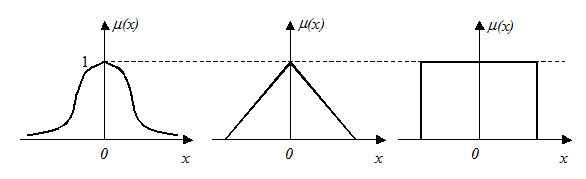
Нечёткие числа L-R типа. Нечёткие числа (L-R)- типа (Left- Right) это разновидность нечётких чисел специального вида, задаваемых по определенным правилам с целью снижения объёма вычислений при операциях над ними. Функции принадлежности нечётких чисел (L-R)- типа задаются с помощью не возрастающих на множестве неотрицательных действительных чисел функций действительного переменного L(х) и R(х), удовлетворяющих свойствам: 1) L(-х) = L(х); 2) R(-х) = R(х); 3) L (0) = R(0). К классу (L-R)-функций относятся функции следующего вида:
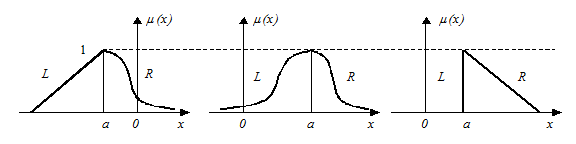
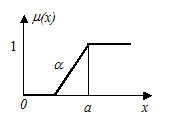
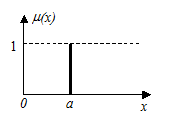
Унимодальное нечёткое число А с модой а (условие mА(а) = 1 справедливо только для одной точки действительной оси) с помощью L(х) и R(х) задаётся следующим образом:
Таким образом, при заданных L(х) и R(х) нечёткое унимодальное число задаётся тройкой параметров (а,
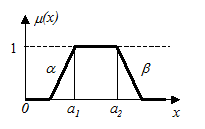
Толерантное нечёткое число задаётся, соответственно, четвёркой параметров (а1 , а2,
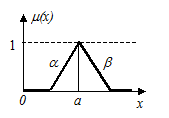
где а1 и а2 – границы толерантности (на интервале [ а1, а2 ] значение функции принадлежности mА(х) = 1) (рисунок 42).
Моделирование сложных систем с применением аппарата нечётких множеств требует выполнения большого объёма операций над разного рода лингвистическими и другими нечёткими переменными. Для удобства исполнения операций, а также для ввода-вывода и хранения данных желательно выбирать функций принадлежности стандартного вида. Нечёткие множества, которыми приходится оперировать в большинстве задач, являются, как правило, унимодальными и нормальными. Одним из возможных методов аппроксимации унимодальных и толерантных нечётких множеств является аппроксимации с помощью функции (L-R)- типа. Примеры (L-R)- представлений некоторых типовых термов лингвистических переменных приведены в таблице.
|

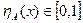 , где
, где 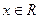
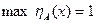 .
.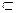 R называется носителем нечёткого числа А, если
R называется носителем нечёткого числа А, если х > 0; и А отрицательно, если
х > 0; и А отрицательно, если 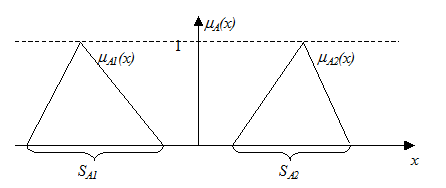
 Пусть L(х) и R(х) - функции (L-R)- типа. Тогда:
Пусть L(х) и R(х) - функции (L-R)- типа. Тогда: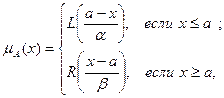
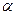 >0,
>0, 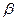 >0 – левый и правый коэффициенты нечёткости.
>0 – левый и правый коэффициенты нечёткости.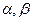 ).
).
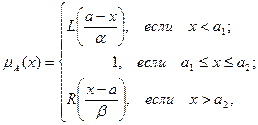

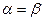 > 0
> 0
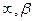 ) LR
) LR
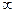

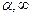 ) LR
) LR
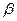 =
= 
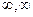 ) LR
) LR