Фильтр восстановления формы сигналов
Коррекция формы выходных сигналов обычно применяется только для кабелей небольшой длины при прямой передаче сигналов геофизических детекторов на измерительные приборы. С учетом этого, все нижеследующие расчеты выполняются в качестве примера для кабеля КГ 1х0.75-55-150 длиной 2 км. Общая методика синтеза фильтров ЧД (которая в следующем разделе будет использоваться и для расчетов фильтров ЧД кодовых импульсных сигналов) включает следующие операции: 1. Задание длины кабеля, определение его импульсного отклика и сдвиг отклика (по началу значимых значений фронта) в начало координат. Сдвинутую функцию будем считать амплитудным откликом h(t) кабеля (без учета задержки сигнала) и выполняем преобразование Фурье h(t) Þ H(w). 2. Задание формы выходного импульса z(t) фильтра ЧД в виде гауссовской функции (или любой другой с ограниченным и быстро затухающим спектром) и определение его спектра z(t) Û Z(w). Временное расположение импульса z(t) должно быть таким, чтобы площадь импульса практически полностью располагалась за пределами фронта импульсного отклика кабеля h(t). Максимум z(t) должен располагаться за максимумом отклика кабеля. В принципе, он может задаваться на максимуме и до максимума импульсного отклика, но это ухудшает параметры оператора ЧД. Площадь z(t) при метрологической коррекции сигналов должна быть равна площади импульсного отклика. При восстановлении кодовых сигналов этот параметр не нормируется.
Рис. 15.1.1. Форма импульсов. На рис. 15.1.1 приведены примеры формы сигналов, нормированные по амплитуде к 1 для наглядности сравнения. Ширина гауссовского импульса (значение стандарта – среднеквадратического отклонения от центра импульса) подбирается по допустимому коэффициенту усиления дисперсии шумов (после расчета оператора ЧД). Для приведенных далее расчетов площади импульсов установлены равными, ширина импульса z(t) установлена такой, чтобы коэффициент усиления дисперсии шумов был не более 4 (амплитудное усиление шумов не более 2), при этом амплитудное усиление сигналов порядка 4.7, что позволяет повысить отношение сигнал/шум не менее чем в 2 раза. 3. Вычисление спектральной плотности передаточной функции фильтра ЧД, которое выполняется по формуле: Hd(w) = Z(w)/H(w). (15.1.1)
При равных площадях импульсного отклика кабеля и функции z(t) значения спектров Z(w) и H(w) при w=0 равны и, соответственно, их отношение равно 1, т.е. коэффициент усиления фильтром ЧД постоянной составляющей равен 1. Для фильтров ЧД кодовых импульсов этот параметр не регламентируется. Более того, при коэффициенте усиления постоянной составляющей менее 1 фильтр ЧД в определенной мере стабилизирует нулевую линию сигналов. Функция Hd(w) имеет смысл в области значимых значений H(w) и за пределами этой области обнуляется, что исключит усиление высокочастотных шумов кабеля. Усечение, начиная с определенной частоты wc, целесообразно выполнять весовой гауссовской функцией: Hd(w) = Hd(w)×exp(-a(wc+w)2), w ³ wc. (15.1.2) Пример формы спектральной плотности фильтра ЧД приведен на рис. 15.1.2 в сопоставлении со спектрами исходных импульсов (масштаб спектров импульсов для наглядности увеличен). Пунктиром на рисунке показана усеченная часть функции Hd(w). Коэффициент усиления фильтром дисперсии входных статистических шумов при равномерном распределении шумов в диапазоне от 0 до W: Ke = (1/W) По рисунку 15.1.2 нетрудно сделать заключение, что коэффициент усиления фильтром ЧД дисперсии статистических шумов больше 1 и существенно зависит от эффективной ширины спектра импульса z(t). Чем меньше значение DW импульса z(t) (больше эффективная ширина DT импульса), тем меньше коэффициент усиления дисперсии шумов.
Рис. 15.1.3. Оператор ЧД. 4. Обратным преобразованием Фурье функции Hd(w) вычисляется оператор фильтра ЧД: Hd(w) Þ hd(t). Пример оператора, нормированного на интервал дискретизации данных Dt = 0.1 мкс для цифровой обработки сигналов, приведен на рис. 15.1.3 и получен по исходной функции Hd(w) рис. 15.1.2. Коэффициент усиления дисперсии шумов данного оператора равен 3,4. При заданном на рис. 15.1.1 коэффициенте усиления амплитуды импульса z(t) порядка 4.7 это дает улучшение отношения сигнал/шум в 4.7/ При подаче на вход кабеля импульса Кронекера do на выходе фильтра будем иметь: s(t)=do*h(t)*hd(t) Û 1×H(w)×Hd(w)=Z(w) Û z(t), т.е. выходной единичный импульс вместо асимметричной формы импульсного отклика кабеля будет иметь симметричную форму гауссовского импульса. Аналогичным является и результат непосредственной свертки импульсного отклика с оператором фильтра ЧД, что может использоваться для контроля расчетов операторов фильтров ЧД. Точность воспроизводства формы заданной функции выходного импульса определяется размером оператора ЧД, который имеет существенное значение при его технической реализации в виде трансверсальных фильтров на линиях задержки. Основная часть энергии оператора (более 99%) сосредоточена в пределах интервала, примерно равного (2-3) значениям фронта импульсного отклика, т.е. начальная часть импульсного отклика содержит практически всю информацию о форме сигналов на входе кабеля. Однако, вследствие достаточно длинного спада отклика с постепенным уменьшением скорости спада, ограничение размера оператора ЧД короткой значимой частью приводит к появлению на его выходе послеимпульсных «выбросов» с амплитудным значением до 2% от максимальной амплитуды выходного сигнала (чем меньше размер оператора ЧД, тем больше амплитуда выбросов) и c длительностью, равной соответствующей длительности значимой части импульсного отклика (с постепенным затуханием). Положение послеимпульсного "хвоста" (включая первый отрицательный выброс) относительно нулевой линии может смещаться изменением концевого значения оператора ЧД.
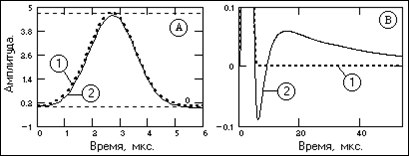
Рис. 15.1.4. Свертка импульсного отклика с оператором ЧД. На рис. 15.1.4 приведены результаты свертки (кривая 2) импульсного отклика кабеля с оператором ЧД размером 4.2 мкс при временной длине значимой части импульсного отклика кабеля (более 0.01 максимального значения) порядка 70 мкс. Кривая 1 – заданная функция z(t). Как видно на графике А, форма заданного импульса сжатия реализуется достаточно точно. Среднее квадратическое расхождение с заданной формой z(t) – 0.024, отрицательный выброс не более 2% от амплитуды при центрировании "хвоста" относительно нулевой линии (график B). На рис. 15.1.5 приведено сопоставление формы импульсов на входе кабеля, заданных на интервалах 2DTk, на выходе кабеля (на входе фильтра ЧД) и на выходе фильтра ЧД. Для фильтрации использован оператор ЧД, приведенный на рис. 15.1.3, размером 4.2 мкс. Амплитудные значения сигналов на входе кабеля умножены на площадь импульсного отклика (учет безвозвратных электромагнитных потерь), и сдвинуты во времени для сопоставления формы к сигналам на выходе фильтра ЧД.
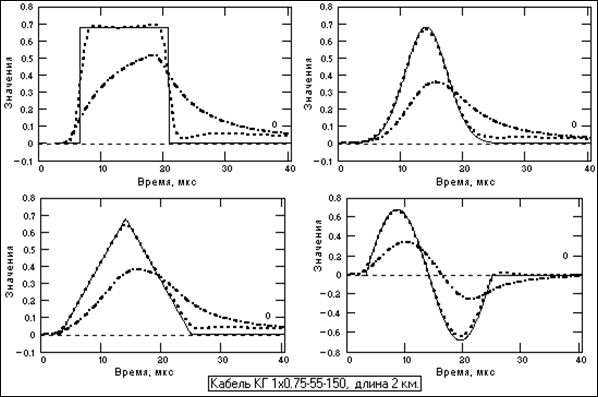
Рис. 15.1.5. Формы сигналов на входе (сплошные линии), на выходе кабеля (штрих-пунктир) и на выходе фильтра ЧД (пунктир). Входные сигналы смещены во времени. Как видно на графиках, форма сигналов со значением DW, соизмеримом и меньшим значения DWk, восстанавливается достаточно хорошо (со среднеквадратической погрешностью в пределах сигнала не более 1% относительно амплитудного значения), но для однополярных сигналов значение накопленного послеимпульсного «хвоста» возрастает до 5% от амплитуды сигнала. Если «хвост» послеимпульса должен быть ограничен по амплитуде определенной величиной, то это выполняется увеличением размера оператора фильтра ЧД. При длине оператора, равной длине импульсного отклика кабеля, амплитуда послеимпульса уменьшается более чем на порядок. Для прямоугольных импульсов при DW > DWк погрешность, естественно, возрастает за счет сглаживания фронтов, но остается в пределах не более (2-3)% по амплитудным значениям. Усиление шумов. На рис. 15.1.6 приведены графики модельного статистического шума на входе (сплошная линия) и на выходе (пунктир) фильтра ЧД с параметрами, описанными выше. По результатам моделирования коэффициент усиления дисперсии шумов полностью соответствует расчетному значению (расчетное – 3.4, модельное на односекундном интервале – 3.38). Фильтр ЧД сглаживает шумы в соответствии со своей частотной характеристикой, и форма выходных шумов становится похожей на форму произвольных сигналов.
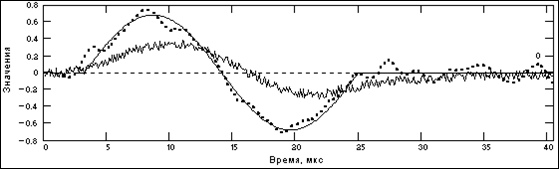
Рис. 15.1.6. Форма шумовых сигналов на входе и на выходе фильтра ЧД (пунктир). Усиление шумов может существенно усложнить метрологическое восстановление произвольных сигналов. На рис. 15.1.7 приведен пример фильтрации зашумленного сигнала при среднеквадратическом уровне шума порядка 10% от амплитудных значений входного сигнала. Заметим, что хотя частотный диапазон спектра статистических шумов на выходе кабеля значительно превышает частотный диапазон сигналов, любые линейные методы фильтрации сигналов (подавления шумов) в данном случае не имеют смысла. Оператор ЧД, как это следует из (15.1.2) и можно видеть на рис. 15.1.2, самостоятельно подавляет все высокочастотные шумы.
Рис. 15.1.7. Форма сигнала с шумом на входе и на выходе фильтра ЧД (пунктир). При использовании цифровых методов обработки данных плавная форма выходных информационных сигналов с априорно известными параметрами их динамики позволяет использовать до подачи сигналов на фильтр ЧД нелинейные методы фильтрации, и в частности – адаптивные фильтры, не изменяющие динамики информационных сигналов при подавлении шумов, в том числе перекрывающихся по частотному диапазону с частотным диапазоном сигналов.
|

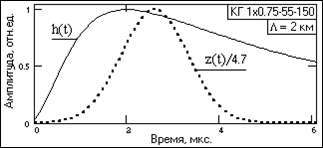
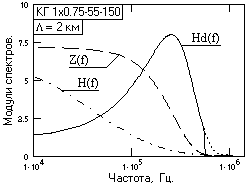 Рис. 15.1.2. Спектры импульсов.
Рис. 15.1.2. Спектры импульсов.
 |Hd(w)|2 dw. (15.1.3)
|Hd(w)|2 dw. (15.1.3)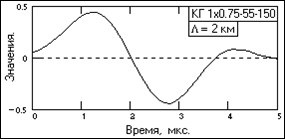
 » 2.5 раза при равномерном распределении шумов в интервале от 0 до W = 1/(2Dt).
» 2.5 раза при равномерном распределении шумов в интервале от 0 до W = 1/(2Dt).