Пример проведения анализа и синтеза логических цепей
Пусть необходимо построить мажоритарную ячейку (ячейку голосования) на три входа, т. е. такую ячейку, у которой сигнал на выходе равен единице тогда, когда на двух или трех входах цепи присутствует сигнал единицы, в противном случае выходной сигнал должен быть равен нулю. Вначале заполним таблицу истинности (табл. 5.5). Поскольку в данном случае имеются три входных сигнала х1, х2, х3, каждый из которых может принимать одно из двух возможных значений (0 или 1), то всего может быть восемь различных комбинаций этих сигналов. Четырем из этих комбинаций будет соответствовать выходной сигнал F, равный единице. Пользуясь данными табл. 5.5, можно записать логическую функцию, которую должна реализовать синтезируемая цепь. Для этого нужно представить функцию в виде суммы логических произведений, соответствующих тем строкам табл. 5.5 (3, 5–7), для которых функция F равна единице. Аргументы записываются без инверсии, если они равны единице, и с инверсией, если равны нулю.
Таблица 5.5 Таблица истинности для составления логической функции
Если в синтезируемой таблице истинности выходная величина чаще принимает значение «1», то синтезируются строки, в которых выходная величина равна «0». При выполнении заданной процедуры получим функцию F= Для минимизации (упрощения) данной функции нужно применить основные законы алгебры логики. Возможна следующая последовательность преобразований, например, с применением закона склеивания (теоремы де Моргана): F = + Как видно, полученное конечное выражение гораздо проще исходного. Аналогично проводится анализ (составление таблиц истинности) и более сложных логических схем. Для выполнения задания предлагается набор наиболее распространенных логических элементов (рис. 5.5).
Рис. 5.5. Набор логических элементов для выполнения задания
|

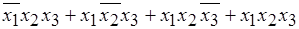 . (5.1)
. (5.1)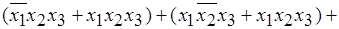
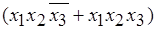 =
= 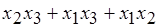 . (5.2)
. (5.2)



