МОСКОВСКИЙ АВИАЦИОННЫЙ ИНСТИТУТ
(НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ)
Расчетно - графическая работа по курсу КОМБИНАТОРНЫЙ АНАЛИЗ На тему: Преобразование произвольного вершинного графа к квазиканонической форме Вариант 21
Работа выполнена студентом гр. 60-101 Ивановым И.А. Работу консультировали преподаватели Малинина Н.Л., Демидова О.Л. Москва 2012 год
Задание 1. Задание 2. Задание 3. Задание 4. Задание 5. Нормализация графа. Для своего варианта по матрице смежности нарисовать граф. Исходные данные: матрица
Рис. 1 Подсчитать, сколько всего может получиться вариантов различных графов из такого набора элементов, имея в виду, размер матрицы, количество вершин графа и условие их размещения в верхней правой треугольной подматрице.
Нарисовать и перечислить все возможные пути и контуры в графе (примерное оформление).
Выделить в исходном графе несколько подграфов и частичных графов
Сделать нормализацию графа. 2. Импортируем данные матрицы в электронные таблицы (рис. 2а):
Рис. 2 Строка внизу - суммы по столбцам 3. По формулам считаем матрицу 4. Далее считаем матрицу 5. По результатам расчетов формируем матрицу 6. Делаем нормализацию, т.е. добавляем к матрице
Рис. 3 7 Импортируем данные в электронные таблицы еще раз (рис. 4) и снова считаем матрицы
Рис. 4 Результаты вычислений можно посмотреть, активизировав электронные таблицы. В целях упрощения записи формул было изъято умножение на единицу. На результат это не влияет, но запись формулы сокращается. Покажем результаты первого этапа нормализации на графе (рис. 5б).
Рис. 5 Из результатов расчетов видно, что нормализацию следует сделать еще раз, поскольку в матрице остался элемент
Рис. 6 Снова считаем матрицы
Рис. 7 Наконец, видно, что процесс нормализации пришел к завершению. Теперь займемся упорядочиванием графа. Что это такое? Имея в виду, что наш граф - это сложная система, да еще такая, которую мы хотим анализировать с помощью компьютера, мы должны знать точный порядок выполнения операций, чтобы не прийти в Как это делается? Приступим. Первое. Матрица должна иметь в точности один пустой столбец и одну пустую строку[ЧП1]. Пустому столбцу приписываем № 1. Этот же номер присваивается соответствующей строке. Номер столбца вписывается в дополнительную строку Операция 3. Общий шаг. Просматриваем первую пронумерованную строку и исключаем из нее элементы, которые в ней содержатся. В нашем случае обведем их в кружочки. Это будут элементы Операция 4. Рассмотрим подмножество непронумерованных столбцов, имеющих вычеркнутые элементы. На этом этапе упорядочения это будут столбцы Операция 5. Матрица переписывается с новым порядком рядов (рис. 11б). Порядок рядов становится понятным из рисунка 11б.
рис. 8 Операция 3. Общий шаг. Просматриваем следующую пронумерованную строку (в этот момент это будет строка 2) и исключаем из нее элементы, которые в ней содержатся. В нашем случае обведем их в кружочки. Это будут элементы Операция 5, 6, 6 и 8. Упорядочены дуги Снова переписываем матрицу с новым порядком рядов (рис. 12б).
Рис. 9 Полученная матрица упорядочена по слоям, но внутри слоев вершины не упорядочены. Следовательно, неупорядочена еще и некоторая часть дуг. Поэтому переходим к нумерации дуг и вершин графа (сетевой модели).
Рис. 10 Операция 6. Номера рядов матрицы, которые мы получили перед этим в операциях 2, 3 и 4 - это, с одной стороны, - номера подматриц, на которые распадается матрица, а, с другой стороны, - это номера начальных событий для тех работ, которым соответствуют столбцы матрицы (рис. 12). Рис. 11 Упорядочение
|

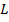 (рис. 1а) и граф
(рис. 1а) и граф  (рис. 1б):
(рис. 1б):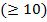 .
.
 ; столбец слева - суммы по строкам
; столбец слева - суммы по строкам 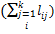 . Их считают с помощью функции СЧЕТ(«диапазон»).
. Их считают с помощью функции СЧЕТ(«диапазон»). (рис. 2б).
(рис. 2б). , например, элемент
, например, элемент  . Минимальное значение любого элемента в этой же матрице в этой строке тоже будет равно
. Минимальное значение любого элемента в этой же матрице в этой строке тоже будет равно  по сравнению с другими элементами в этой же строке буде равно
по сравнению с другими элементами в этой же строке буде равно  . Аналогично превышение этого элемента по сравнению с другими в этом же столбце будет равно
. Аналогично превышение этого элемента по сравнению с другими в этом же столбце будет равно  . Следовательно,
. Следовательно,  .
. ,
, 
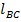 ,
,  и
и  . На матрице
. На матрице  (первое приближение нормализации)
(первое приближение нормализации)

 , который отличается от нуля. Добавляем к матрице еще одну строку и один столбец. Заменяем элемент
, который отличается от нуля. Добавляем к матрице еще одну строку и один столбец. Заменяем элемент  на два элемента
на два элемента  и
и  . Результаты второго этапа нормализации видно из рис. 6.
. Результаты второго этапа нормализации видно из рис. 6.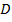 , не имея достаточно данных, чтобы сделать ту работу, которая у нас закодирована буквой
, не имея достаточно данных, чтобы сделать ту работу, которая у нас закодирована буквой 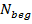 под матрицей и в дополнительный столбец
под матрицей и в дополнительный столбец  и
и 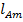 .
. и
и 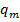 . Вычеркнутые на первом этапе элементы входят в подматрицу. Всем соответствующим столбцам присваивается очередной номер, в данном случае №2 (рис. 11а). Этот же номер присваивается соответствующим строкам. На этом этапе №2 получат столбцы
. Вычеркнутые на первом этапе элементы входят в подматрицу. Всем соответствующим столбцам присваивается очередной номер, в данном случае №2 (рис. 11а). Этот же номер присваивается соответствующим строкам. На этом этапе №2 получат столбцы  и
и 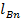 (рис. 12а). Эти столбцы получат №3.
(рис. 12а). Эти столбцы получат №3.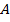 и
и  и вершины 1 и 2. Просматриваем вторую строку (столбцы
и вершины 1 и 2. Просматриваем вторую строку (столбцы 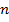 ). Второй общий шаг - пронумерована вершина 3. Дуга
). Второй общий шаг - пронумерована вершина 3. Дуга 


