Приведенная стоимость

 

Для оценки движения финансовых потоков во времени применяют различные формулы финансовой математики, в том числе и расчет приведенной стоимости или метод дисконтированных денежных потоков.

Дисконтирование является обратной операцией расчета сложных процентов. В то время, когда инфляция больше нуля, деньги сегодня стоят дороже чем завтра. Для того чтобы определить сегодняшнюю стоимость денег и применяют дисконтирование денежных потоков.

Сущность расчета заключается в том, что планируемые к получению в будущем деньги пересчитываются в сегодняшнюю стоимость, с учетом количества периодов и ставки дисконтирования, по формуле обратной расчету сложных процентов.

 

Ставка дисконтирования (discount rate, учетная ставка, дисконтная ставка, дисконт) - процентная ставка, используемая для определения текущей стоимости будущих денежных потоков. Ставка дисконтирования рассчитывается отношением будущей стоимости за 1 период, за вычетом текущей, к будущей стоимости ((FV-PV) /FV).

 

Например, планируемые к получению 1000 рублей через 1 год инвестирования при ставке дисконтирования 15% эквивалентны сегодняшним 869,57 рублям; для планируемых к получению 1000 рублей через 2 года инвестирования при ставке дисконтирования 15% эквивалентны сегодняшним 756,14 рублям; для планируемых к получению 1000 рублей через 3 года инвестирования при ставке дисконтирования 15% эквивалентны сегодняшним 657,52 рублям.

 

В данном примере величина 869,57 рублей является текущей стоимостью величины 1000 рублей, полученных от инвестиции сроком на 1 год при ставке дисконтирования 15%.

 

Формула для расчета дисконтированного денежного потока:

 

PV - текущая стоимость;

FV - будущая стоимость;

r - ставка дисконтирования;

t - количество лет.

Чем дольше срок получения инвестиции и чем выше ставка дисконтирования, тем меньше текущая стоимость.

 

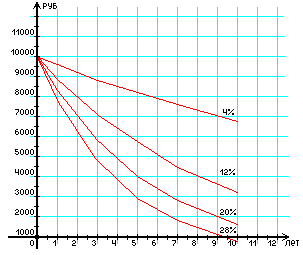
Рис. 2. График приведенной стоимости; текущие стоимости: начальная сумма 10 000 руб., ставка дисконтирования 4, 12, 20, 28% годовых

 

На тему этой методики существуют примеры задач на приведенную стоимость с решениями.

 

ЗАДАЧА

На сумму 15 тыс. р. в течении 4-х лет ежегодно начисляются простые проценты по процентной ставке 40% годовых, а на все начисленные проценты ежегодно осуществляется наращивание сложных процентов по процентной ставке 30% годовых. Определить величину наращенной суммы в конце 4-го года.

 

Решение

1) Сумма %-а по простой ставке получилась 6000 за каждый год. И соответственно именно 6000 р. будут в сложных вращаться 3 года. т.е.

S=6000(1+0,3)^3=7800

То есть S1 = 15 000 * 0,4 = 6 000 р. проценты ежегодно.

 

2) Начисление сложных процентов на проценты нужно рассматривать как три ежегодных вклада.

Т.е. первые 6 000 принесут 6 000 * (1+0,3)^3 - 6 000

вторые: 6 000 * (1+0,3)^2 - 6 000

и третьи: 6 000 * (1+0,3)^1 - 6 000

 

Значит расчет будет таким:

S2 = 6000*(1+0,3)^3 - 6 000 + 6000*(1+0,3)^2 - 6 000 + 6000*(1+0,3)^1 - 6 000=

= 6000*(1+0,3)*((1+0,3)^2+(1+0,3)+1) - 18 000 =

= 6000 * 1,3 * (1 + 0,6 + 0,09 +1 +0,3 + 1) - 18 000 =

=6000 * 1,3 * 3,99 - 18 000 = 31 122 - 18 000 = 13 122р.

 

Общая сумма процентов по вкладу:

S = 6 000*3 + 13 122 = 31 122 р.