Расчет крепежных резьбовых соединений

Основным критерием работоспособности крепежных резьбовых соединений является прочность. Стандартные крепежные детали сконст­руированы равнопрочными по следующим параметрам: по напряжениям среза и смятия в резьбе, напряжениям растяжения в нарезанной части стержня и в месте перехода стержня в головку. Поэтому для стандартных крепежных деталей в качестве главного критерия работоспособности принята прочность стержня на растяжение, и по ней ведут расчет болтов, винтов и шпилек. Расчет резьбы на прочность выполняют в качестве проверочного лишь для нестандартных деталей.

При расчете резьбы условно считают, что все витки нагружены одинаково, а неточность в расчете компенсируют значением допускаемого на­пряжения.

Условие прочности резьбы на срез имеет вид:

τ_ср= Q/A_cp < [τ_ср]

где Q — осевая сила; А_ср — площадь среза витков нарезки; для винта (рис. 1) A_ср = πd_lkH_r,для гайки А_cp= πDkH_r. Здесь H_r — высота гайки; к — коэффициент, учитывающий ширину основания витков резьбы. Если винт и гайка из одного материала, то на срез проверяют только винт, так как d₁<D.

Условие прочности резьбы на смятие имеет вид:

σ _см= Q/A_cм <[ σ_см ]

 

где А_cv — условная площадь смятия (проекция площади контакта резьбы винта и гайки на плос­кость, перпендикулярную оси): А_см = πd₂hz, где (рис. 1) πd₂ — длина одного витка по сред­нему диаметру; h — рабочая высота профиля резь­бы; z = H_r /р — число витков резьбы в гайке вы­сотой H_г; р — шаг резьбы.

 

Расчет резьбовых соединений при различных видах нагружения

1.Расчет незатянутых болтов

Рис. 2

Характерный пример незатянутого резьбового соединения — крепление крюка грузоподъемного механизма (рис. 3.15). Под действием силы тяжести груза Q стержень крюка работа­ет на растяжение, а опасным будет сечение, ослабленное нарезкой. Ста­тическая прочность стержня с резьбой (которая испытывает объемное напряженное состояние) приблизительно на 10% выше, чем гладкого стержня без резьбы. Поэтому расчет стержня с резьбой условно ведут по расчетному диаметру d_p=d- 0,9 р, где р — шаг резьбы с номинальным диаметром d (приближенно можно считать d_p = d₁). Условие прочности нарезанной части стержня на растяжение имеет вид:

σ_р = Q/A_р <[ σ_р]

где расчетная площадь А_р= πd_р²/4.

Расчетный диаметр резьбы:

 

2. Расчет затянутых болтов

Рис. 3

Пример затянутого болтового соединения — креп­ление крышки люка с прокладкой, где для обеспечения герметичности необходимо создать силу затяжки Q (рис. 3). При этом стержень болта растягивается силой Q и скручивается моментом М_р в резьбе.

Напряжение растяжения

σ_р = Q/(πd_p² /4),

максимальное напряжение кручения

τ_к = M_p/W_p,

где W_p = 0,2d_p³ — момент сопротивления круче­нию сечения болта; М_р=0,5Q d₂ tg(ψ + φ'). Подставив в эти формулы средние значения угла подъема ψ резьбы, приведенного угла трения φ' для метрической крепежной резьбы и применяя энергетическую теорию прочности, получим

σ_экв=√(σ_р² + 3τ_к²)= 1,3 σ_р

Отсюда, согласно условию прочности σ_экв < [σ_р ], запишем

σ_экв = 1,3 Q/(πd_p² /4)= Q_расч /(πd_p² /4) < [σ_р ],

где Q_расч =1,3Q, а [σ_р] — допускаемое напряжение при растяжении.

Таким образом, болт, работающий на растяжение и кручение, можно условно рассчитывать только на растяжение по осевой силе, увеличенной в 1,3 раза. Тогда

d_p > √1,3 ∙ 4Q_расч /π[σ_р ]

3.Расчет болтовых соединений, нагруженных поперечной силой

а) Болт поставлен без зазора

В этом случае отверстие калибруют разверткой, а стержень болта выполняют с допуском, обеспечивающим беззазорную посадку. В этом случае пренебрегают силами трения в стыке, т.к. затяжка болта необязательна. Болт рассчитывают на срез и смятие.

 

Рис. 4

Условие прочности на срез:

τ_cp = 4F/(πd_p²i)<[ τ_cp],

Условие прочности на смятие:

σ_см = F/(d₀δ)<[ σ_см],

где i — число плоскостей среза (для схемы на рис. 4 i = 2); d_oδ - условная площадь смятия, причем если δ>(δ₁ + δ₂), то в расчет (при одинаковом материале деталей) принимается меньшая величина. Обычно из условия прочности на срез определяют диаметр стержня болта, а затем проводят проверочный расчет на смятие.

б) Болт поставлен с зазором

Рис. 5

Внешнюю нагрузку F уравновешивают силами трения в стыке, которые образуются вследствие затяжки болта. Рассматривая равновесие детали 1 получим условие отсутствие сдвига деталей в стыке:

или

где i – число плоскостей стыка;

k - коэффициент запаса прочности;

f – коэффициент трения.

Прочность болта оценивают по эквивалентным напряжениям ():

Внешняя нагрузка на болт не передается, поэтому болт рассчитывают только на статическую прочность по силе затяжки, даже при переменной внешней нагрузке.
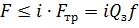