Используя постулаты и принимая во внимание, что
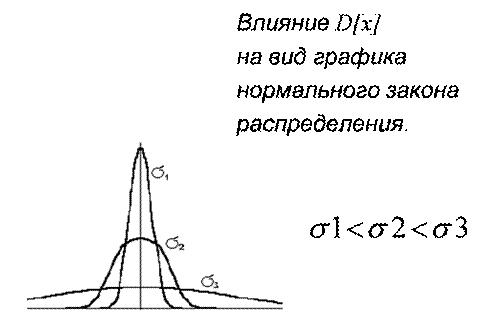
· измерения без погрешности невозможно; · случайные погрешности являются событиями независимыми. à;Все результаты измерений взаимно независимы; · число измерений очень велико и все измерения выполняются равноточно; Гаусс вывел НОРМАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ плотности вероятности случайных погрешностей.
№ 19. Вероятность попадания случайной погрешности в интервал. Придельное значение погрешности
интеграл вероятности (интеграл Фурье, функция Лапласа).
Свойства интеграла Фурье 1. 2. 3.
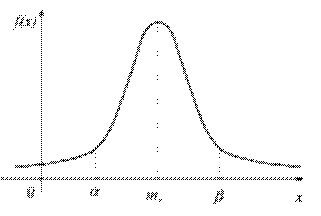
4. Нормированная функция Лапласа: 2. Найдем вероятность попадания СП в полный интервал:
Например: · t=1; a=s; P(– s <x< s )=2Фо(1)=0,683 · t=2; a=2s; 2Фо(2)=0,9545 · t=3; a=3s; 2Фо(3)=0,9973 Величину 3s называют ПРЕДЕЛЬНОЙ ПОГРЕШНОСТЬЮ. Замечание 1: Функцию Лапласа при наличии систематического сдвига вычисляем по следующей формуле:
Замечание 2: Частный случай: Замечание 3: Результирующая погрешность часто складывается из ряда составляющих с различными плотностями распределения: В связи с этим возникает задача нахождения суммарного закона распределения погрешности. Для суммы: №20. Метрологические характеристики прибора с последовательной структурной схемой – случай линейных звеньев. СИ состоят из нескольких ИП (звеньев) и все метрологические характеристики (МХ) СИ определяются: · составом СИ, · МХ каждого звена, · и зависят от положения звена в составе СИ. СТРУКТУРНАЯ СХЕМА СИ – условное изображение последовательности ИП, входящих в состав СИ в порядке их взаимодействия в цепи. Рассмотрим случай только статического режима работы как отдельных ИП входящих в состав СИ, так и средства измерения в целом.
|
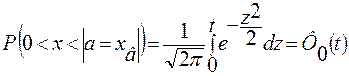
- площадь фигуры, опирающейся на нулевое основание равна 0.
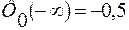
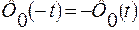- функция нечетная. Докажем:
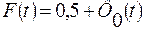
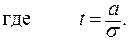
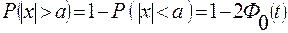
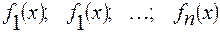
, независимых непрерывных случайных величин, имеющих распределения 
, суммарный закон распределения погрешности называется композицией.
