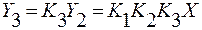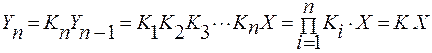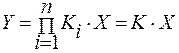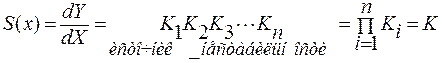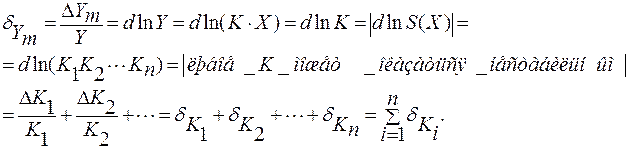Случай линейных звеньев

К1, K2, …, Кn – ПОСТОЯННЫЕ коэффициенты преобразования отдельных звеньев (линейная функция преобразования);

Функция преобразования средства измерений:

Чувствительность СИ:

Средства измерения прямого преобразования обладают ВЫСОКОЙ ПОСТОЯННОЙ чувствительностью. – ЭТО ПРЕИМУЩЕСТВО.

Погрешность СИ прямого преобразования:

· Аддитивная погрешность: общая абсолютная аддитивная погрешность, приведенная к выходу прибора.

Аддитивная погрешность каждого отдельного ИП (звена) полностью входит в погрешность СИ (результата) и при большом числе последовательных звеньев общая погрешность велика – ЭТО НЕДОСТАТОК.

· Мультипликативная погрешность: обусловлена нестабильностью чувствительности СИ.

Погрешность каждого отдельного ИП (звена) полностью входит в погрешность СИ – ЭТО НЕДОСТАТОК.

ВЫВОД:приборы с последовательной структурной схемой не обладают достаточной точностью, т.к. погрешности отдельных звеньев (как аддитивные, так и мультипликативные) суммируются.

 

№21. Метрологические характеристики прибора с последовательной структурной схемой – случай нелинейных звеньев

СИ состоят из нескольких ИП (звеньев) и все метрологические характеристики (МХ) СИ определяются:

· составом СИ,

· МХ каждого звена,

· и зависят от положения звена в составе СИ.

СТРУКТУРНАЯ СХЕМА СИ – условное изображение последовательности ИП, входящих в состав СИ в порядке их взаимодействия в цепи.

Рассмотрим случай только статического режима работы как отдельных ИП входящих в состав СИ, так и средства измерения в целом.