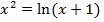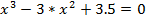Геометрическая интерпретация
Рассмотрим график функции
И следующая итерация
Уравнение: 1. 2. Программа1: FUNCTION f(x) implicit none real(8):: x real(8):: f f = x**2-log(x+1) RETURN END FUNCTION
function p(x) implicit none real(8):: x real(8):: p p = log(x+1)/x return end function
Program Equations implicit none real(8):: x11,x12,x21,x22,lam real(8):: f,p integer:: i real(8):: eps = 0.0000001 open(2,file='Eq_log.txt') print '(A)', 'Insert ends of interval: ' read *, x11,x12 x21=x11 x22=x12 lam = (x12-x11)/(f(x12)-f(x11)) write(2,*) 'Секущие' i=0 do while (abs(x11-x12) > eps) i=i+1 x11=x12 x12=x11-lam*f(x11) write(2,*) i, ' ', x12 end do write(2,*) 'Итерации' i=0 do while (abs(x22-x21)>eps) i=i+1 x21=x22 x22=p(x21) write(2,*), i, ' ', x22 enddo close(2)
END program Equations Программа2: function f(x) implicit none real(8):: x real(8):: f f = x**2-3*x**2+3.5 return end function
function p(x) implicit none real(8):: x real(8):: p p = x**2/3+3.5/(3*x) return end function
Program Equations implicit none real(8):: x11,x12,x21,x22,lam real(8):: f,p integer:: i real(8):: eps = 0.0000001 open(2,file='Eq_poly.txt') print '(A)', 'Insert ends of interval: ' read *, x11,x12 x21=x11 x22=x12 lam = (x12-x11)/(f(x12)-f(x11)) write(2,*) 'Секущие' i=0 do while (abs(x11-x12) > eps) i=i+1 x11=x12 x12=x11-lam*f(x11) write(2,*) i, ' ', x12 end do write(2,*) 'Итерации' i=0 do while (abs(x22-x21)>eps) i=i+1 x21=x22 x22=p(x21) write(2,*), i, ' ', x22 enddo close(2)
end program Equations
Результаты:Перед написание программы были проверены достаточные условия, найдены производные функций g(x), проверено, что по модулю они меньше 1. 1-е уравнение (на отрезке [0.5,1.5]: i=17 x= 0.74688169556131867(метод секущих) i= 0.74688175835878434(метод простых итераций) 2-е уравнение(на отрезке [1,2]): i=9, x= 1.5579738866642465(метод секущих) i=29 x= 1.5578747884912496(метод простых итераций)
Вывод: в результате проведенной работы были найдены решения двух нелинейных уравнений методом секущих и методом простых итераций. (Был найден только один корень для каждого уравнения.) В результате сравнения полученных результатов было выяснено, что наиболее точным можно считать метод секущих. Решение первого уравнения: 0.747 Решение второго уравнения: 1.558
|

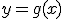 . Это означает, что решение уравнения
. Это означает, что решение уравнения 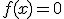 и
и 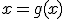 - это точка пересечения
- это точка пересечения 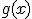 с прямой
с прямой 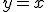 :
:
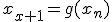 - это координата
- это координата 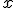 пересечения горизонтальной прямой точки
пересечения горизонтальной прямой точки 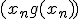 с прямой
с прямой 
 .
.