Основные законы электрических цепей
На рис. 1.7 изображен участок цепи с сопротивлением R. Ток, протекающий через сопротивление R, пропорционален падению напряжения на сопротивлении и обратно пропорционален величине этого сопротивления.
Основными законами электрических цепей, наряду с законом Ома, являются законы баланса токов в разветвлениях (первый закон Кирхгофа) и баланса напряжений на замкнутых участках цепи (второй закон Кирхгофа). В соответствии с первым законом Кирхгофа, алгебраическая сумма токов в любом узле цепи равна нулю:
Возьмем схему на рис. 1.8 и запишем для нее уравнение по первому закону Кирхгофа.
Согласно второму закону Кирхгофа, алгебраическая сумма ЭДС вдоль любого замкнутого контура равна алгебраической сумме падений напряжений в этом контуре
Возьмем схему на рис. 1.9 и запишем для внешнего контура этой схемы уравнение по второму закону Кирхгофа.
Рис.1.10
Получим
Из этого уравнения выведем формулу для тока
В общем виде:
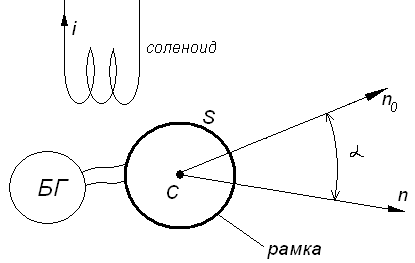
Развитие многих областей науки и техники связано с разработкой и применением магнитных материалов. К таким областям относятся: автоматика; электромашиностроение; радиоэлектроника; вычислительная и измерительная техника. Магнитными измерениями называется область измерительной техники, которая занимается измерением величин, характеризующих магнитное поле, магнитные цепи, магнитные свойства веществ и материалов. К таким величинам относятся: магнитный поток; плотность магнитного потока (индукция); напряженность магнитного поля; магнитный момент; намагничиваемость; восприимчивость; абсолютная (относительная) магнитная проницаемость; магнитное сопротивление и др.; а также исследование их взаимосвязи. Измерение магнитных величин находит применение главным образом в следующих областях: исследование свойств ферромагнитных материалов; исследование и конструирование различных электромагнитных механизмов, приборов, устройств с точки зрения распределения магнитных потоков и намагничиваемости; исследование постоянных магнитов; измерение магнитных полей, создаваемых постоянными магнитами и электромагнитами; исследование параметров магнитного поля земли с целью определения полезных ископаемых; изучение магнитного поля космических объектов; определение физических свойств материалов методом дефектоскопии и др. Магнитные измерения неразрывно связанны с электрическими измерениями, т.к. причина магнитных свойств связана с электрической природой веществ. Основные задачи магнитных измерений: автоматизация процесса измерений; разработка методов контроля; исследование процесса перемагничивания материалов в конкретных условиях работы. 1 Магнитное поле в вакууме и его основные характеристики. 1.1 Индукция магнитного поля. Магнитное поле проявляется в: возникновении ЭДС; возникновении заряда; эффекте Холла. 1.1.1 Опыт с баллистическим гальванометром. Баллистический гальванометр – магнитоэлектрический механизм, у которого противодействующий момент приблизительно равен нулю, а момент инерции – на много больше, чем у обычных гальванометров. Таким гальванометром можно измерять заряд, который проходит через его (гальванометра) рамку. Опыт заключается в следующем: 1) Имеется любой источник магнитного поля (например, катушка). Будем исследовать магнитное поле в точке С. 2) Имеется рамка площадью S, которая соединена с баллистическим гальванометром. Сопротивление цепи r.
Рамку из исследуемой точки будем перемещать в точку А, в которой магнитное поле практически отсутствует и фиксируем заряд, который покажет БГ. По результатам серии опытов можно сделать такие выводы: Заряд не зависит от положения т.А (рамку мы можем переместить в любую другую точку, в которой магнитное поле практически отсутствует); Заряд q пропорционален площади рамки S; Заряд обратно пропорционален сопротивлению контура r; Заряд q зависит от исходного положения рамки – т.е. существует такое направление, при котором при прочих равных условиях заряд q будет максимальным (- направление рамки, при котором проводится опыт); Заряд q пропорционален числу витков соленоида. где В – индукция магнитного поля. Вектор площади определяется следующим образом: Модуль вектора равен площади рамки и направлен перпендикулярно площади рамки таким образом, что если смотреть из острия этого вектора, то обход рамки будет в положительном направлении (против часовой стрелки). Введем новый параметр: где A – магнитный поток. Таким образом, векторное поле индукции В порождает скалярную величину – поток магнитной индукции.
. Это одна из форм записи закона электромагнитной индукции (уравнение максвелла). Оно широко используется для измерения индукции и магнитного потока. Введем еще одну величину – потокосцепление: где число витков рамки. . Попробуем узнать потокосцепление соленоида: где коэффициент пропорциональности. Если размер соленоида не изменится под действием тока, тогда не зависит от времени: Тогда Таким образом, индуктивность соленоида. Она пропорциональна потоку, сцепленному с соленоидом. 1.1.2 Принцип непрерывности магнитного поля. Формула Остроградского.
вычислим поток через замкнутую поверхность, имеющую площадь S. Можно провести такую замкнутую линию L таким образом, чтоб в любой точке справа от L линии магнитной индукции входили в этот объем, а слева – выходили. В каждой части поверхности S выделим очень маленькую площадь. Выберем положительный обход поверхности и представим вектором. Векторы этих площадок всегда направлены от поверхности. Таким образом, вектора и имеют между собой тупой угол. Следовательно, поток, пронизывающий имеет знак «-». Угол между и - острый, поэтому поток, пронизывающий имеет знак «+». Для каждой площади справа от линии L найдется площадь слева от линии, так что суммарный поток через эти площадки = 0. . Перемещая площадь вдоль линий магнитной индукции мы убеждаемся в том, что для любого положения справедливо уравнение. Это нас приводит к выводу о том, что линии магнитной индукции непрерывны и замкнуты. Векторное поле, для которого выполняется это уравнение называется соленоидальным, а векторное поле, для которого выполняется это уравнение – вихревым. Как охарактеризовать способность порождать вектор в каждой точке?
Дивергенция вектора характеризует возможность порождения потока в каждой точке пространства. Предположим, что у нас есть вектор а, который пронизывает замкнутую поверхность S. Обозначим объем, ограниченный площадью S как. Введем новую величину, которая равна: . Эта величина характеризует способность объема порождать вектор. Устремим к нулю и выведем величину – дивергенция вектора, которая определяется этим уравнением. 1.1.3 Формула Остроградского , где замкнутая поверхность; объем, который заключен в замкнутой поверхности. Формула позволяет заменить интеграл по поверхности интегралом по объему. Как мы знаем:. Следовательно. Последнее уравнение – это еще одна запись принципа непрерывности магнитного поля. 1.1.4 Основные уравнения, связывающие электрические и магнитные величины. Среди основных величин в системе СИ есть одна величина – сила электрического тока, которая позволяет установить вместе с другими единицами единицы измерения электрических и магнитных величин. Формула Ампера. Она используется для установления силы электрического тока: где токи, протекающие по двум проводникам бесконечной длины и бесконечно малого сечения, расположенные на расстоянии b друг от друга; сила взаимодействия на расстоянии 1м; магнитная постоянная, одна из фундаментальных постоянных электромагнитного поля. Для установления магнитной постоянной примем: тогда: - это коэффициент, определяемый выбором системы единиц. Поле движущегося заряда.
Сконструируем формулу для вычисления индукции, будем при этом учитывать: Эта формула содержит. Индукция – величина векторная, зависящая от векторов, следовательно, формула содержит множитель. - пропорционально модулю вектора. Это противоречит опыту – индукция с увеличением расстояния должна уменьшаться, значит нужно добавить такой множитель, чтобы индукция была обратно пропорциональна квадрату расстояния: нужно добавить. Можем записать:. (Эта формула не когерентна, потому что с ее помощью не возможно вывести единицы измерения). Вектор направлен таким образом, что если смотреть из острия этого вектора, то поворот вектора до совпадения с происходит в положительном направлении, т.е. против часовой стрелки. Поворот производится по меньшему углу. Закон Био-Савара-Лапласа.
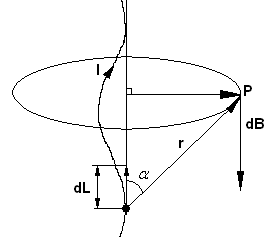
Вычислим индукцию, которая создается элементом проводника в точке Р. По проводнику протекает ток. Сконструируем формулу для вычисления: . Эта формула была получена Лапласом на основании экспериментальных данных, которые были получены Био и Саваром. Формула более универсальна и позволяет вычислить индукцию в точке Р в зависимости от конфигурации проводника. В частности, в случае если проводник выполнен в виде прямой, которая лежит в плоскости доски. Тогда индукция в точке Р, расположенной на расстоянии от проводника:
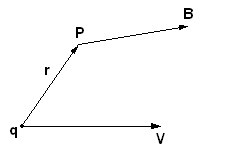
Сила Лоренца. Установлено, что на заряд, движущийся в магнитном поле, действует сила: - это формула подвижного заряда, где заряд; скорость движения заряда; индукция. Т.к. сила действует перпендикулярно скорости, то изменить кинетическую энергию тела, которое несет заряд невозможно. Изменяется только направление движения.
Замечания к формуле: сила является только одной из составляющих сил, действующих на заряд. Если есть электрические и магнитные силы, то суммарная сила: , где напряженность эл. поля. это уравнение когерентное – удобное для установления единиц измерения индукции. Если заряд равен 1Кл. и движется со скоростью 1 м/с в равномерном магнитном поле и сила взаимодействия равна 1Н, то индукция магнитного поля принимается равной единице, т.е. 1Тл. Взаимосвязь основных уравнений.
Замечание: Две формулы 1)поле подвижного заряда и 2) Био-Савара-Лапласа взаимосвязаны таким образом, что если принять одно из этих уравнений основным, то другое выводится автоматически. Можно считать, что движение заряда в магнитном поле – это результаты экспериментальных данных, тогда формула Био-Савара-Лапласа выводится автоматически. Из этой формулы видно, что единственным источником магнитного поля является ток (движущий заряд). 1.2 Циркуляция вектора магнитной индукции , где L – замкнутый контур Попробуем вычислить циркуляцию для простейшего случая. Имеется проводник с током, который протекает перпендикулярно плоскости доски. Выберем любой замкнутый контур L, который расположен в плоскости доски. Для вычисления выберем участок dl, индукция в этой точке будет направлена по касательной. Предположим 1)
- в данной формуле 1 виток, если витков много, то умножим на их количество. Рассмотрим частный случай: 2) в каждой точке этого контура
Начинаем обход с точки b по контуру => … один раз, второй раз =>. Этот интеграл равен Циркуляция отлична от нуля только в том случае, если ток пронизывает контур интегрирования L. Если этот контур не пронизывают токи, то циркуляция равна нулю. Таким образом циркуляцию можно рассматривать как меру тока, которая пронизывает контур. Рассмотрим частный случай: 3) предположим контур интегрирования такой:
где –плотность тока I –суммарный ток через этот контур S –площадь, ограниченная замкнутым контуром L. В левой части уравнения интеграл по контуру, а в правой части интеграл по площади, охваченной этим контуром. 1.3 Ротор вектора индукции 1)
В этом случае циркуляция: 2)
Контур интегрирования проходит внутри соленоида. 3)
Предположим, что ток проходит перпендикулярно рисунку и контур интегрирования не пронизывается током.
1.3 Напряженность магнитного поля в вакууме Возьмем уравнение и разделим на: По определению, величину назовем напряженностью магнитного поля в вакууме – H. В результате: Вектор H имеет такое же направление, как и вектор B и отличается от B на какой-то коэффициент. Следовательно, нет смысла вводить еще один вектор напряженности (во всяком случае, для вакуума). Предположим, есть вектор плотности тока, который перпендикулярен каждой точке плоскости рисунка:
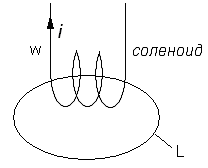
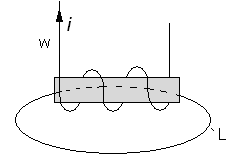
рис.2 j – плотность тока Выбираем точку A и окружаем ее контуром L. Контур L ограничивает (охватывает) площадь S. Вычислим циркуляцию вектора B по контуру L: - циркуляция. Можно сказать, что эту циркуляцию генерирует контур L со своей площадью. Естественно эта циркуляция зависит от площади. (Нам хотелось бы создать такую величину, которая бы характеризовала циркуляцию вектора.) Чтобы оценить способность генерировать циркуляцию в точке A будем стягивать контур L к точке A так, чтобы она (точка A) все время оставалась внутри контура. При этом будем вычислять интеграл: (*) Если, то эту величину (*) называют модулем ротора индукции B. Ротор направлен так, что обход по контуру, если смотреть из острия этого вектора, происходит в положительном направлении. Вывод: как и любое векторное поле, вектор магнитной индукции порождает две величины: скалярная величина; векторная величина; Только для вектора магнитной индукции. Такое поле называется вихревым или соленоидным. Формула Стокса. Позволяет заменить интеграл по контуру интегралом по площади (или наоборот): . Взаимосвязь ротора вектора индукции с вектором плотности тока: (Вернемся к рисунку 2). Ток, пронизывающий площадь, можно вычислить по формуле: (при условии перпендикулярности к доске вектора. При условии другого угла () формула принимает вид:). Следовательно, плотность тока – скаляр, ток – вектор. Учтем формулу . Тогда . В этом уравнении слева – интеграл по контуру, справа – интеграл по площади. Применим формулу Стокса: - интеграл по одной переменной. Перепишем это уравнение следующим образом: Мы получили одно из основных уравнений Максвелла: . Вывод: для вектора магнитной индукции дивергенция = 0, а ротор =. 2 Величины, описывающие поведение магнитных материалов в магнитном поле. 2.1 Намагничиваемость вещества. Мысленно сделаем следующий опыт: предположим, что имеется соленоид, по которому протекает ток. Количество витков соленоида =. Контур интегрирования () проходит внутри соленоида.
Для циркуляции: Эта формула показывает, что единственной причиной поля является ток. В этот соленоид поместим магнитный материал:
Опыт показывает, что магнитное поле в каждой точке контура усиливается, следовательно, индукция в каждой точке увеличится. Если учитывать, что индукция обусловлена потоком, то в правую часть уравнения для второго рисунка при возросшей индукции необходимо добавить слагаемое, которое имеет структуру. Пока назовем элементарным током. Таким образом, для второго рисунка можно написать формулу: Назовем - внешние потоки. Элементарные токи создаются вращающимися электронами, орбиты которых пронизываются контуром интегрирования, а также движущимися зарядами внутри ядра, если контур интегрирования проходит через ядро. Попробуем ответить на вопрос: создаются ли токи всем объемом вещества, или только частью его?
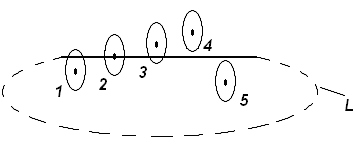
Учитывая рис.2, можно сделать вывод, что а атомы 4, 5 не создают циркуляцию, а 1, 2, 3 – создают. Следовательно, циркуляцию создает «столбик» вещества, который имеет форму цилиндра, диаметр которого равен удвоенному диаметру орбиты электрона, а длина – длине образца.
рис.3 Попробуем ответить на вопрос: как сравнить материалы по способности увеличивать поле? Для того чтоб сравнить материалы, имеющие разную длину по способности «накручивать» токи на контур интегрирования разделим токи на длину образца. Этой величиной можно пользоваться, если она одинакова во всех точках вещества. Если это условие не выполняется, переходим к характеристике в каждой точке:, где бесконечно малое приращение тока; бесконечно малая длина. Эта величина называется намагниченностью вещества, вернее его модуль. Модуль намагничиваемости вещества () направлен так же как и индукция и определяется по формуле: Физический смысл: это ток, накручиваемый на контур интегрирования длиной 1 метр. Модуль для хороших материалов может достигать. 2.2 Напряженность магнитного поля. Вернемся к уравнению. Для рис.3: - поскольку токи распространяются только по длине acb мы можем распространить по всему контуру. С учетом последнего уравнения запишем:. Разделим обе части на:. Объединим интегралы в правой и левой части:. По определению величина равна напряженности магнитного поля:. Напряженность и модуль намагничиваемости имеют одинаковые единицы измерения (). Если нет магнитного вещества, то и мы получаем уравнение, которое не противоречит напряженности в вакууме:. Напряженность создается внешним воздействием (током) и не зависит от свойств материала. При магнитных измерениях стараются выбрать такой метод, чтобы было одинаковым по всему контуру интегрирования.
1.
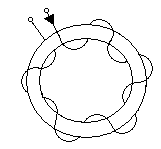
На кольцевую форму образца равномерно наносится обмотка. 2. Если длина катушки достаточно превышает ее диаметр, то есть точные формулы расчета напряженности.
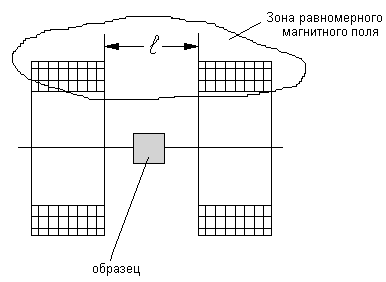
Эта схема позволяет исследовать не замкнутые пластины. 3. Кольцо Гельмгольца.
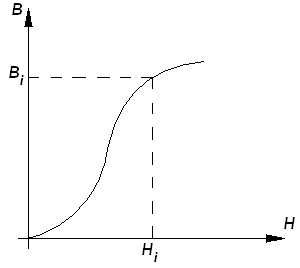
Преимуществом, по сравнению с предыдущим вариантом, является то, что посередине есть пространство, в которое свободно можно внести образец (тело). Если постоянно () то напряженность не всегда следует измерять, ее можно задать, установить с помощью амперметра и коэффициента, зависящего от геометрических размеров образца т.е. коэффициента пропорциональности: . Выводы: Три вектора: индукция, напряженность и намагниченность полностью определяют поведение материала в магнитном поле. Вектор определяет вектор индукции, который создается самим веществом. Вектор определяет часть вектора (), которая создается внешними токами (токам намагничивания). Вектор характеризует суммарное магнитное поле в веществе, создаваемое как внешним, так и внутренним воздействием. Размерность и отличается от размерности, но мы можем всегда привести их к одной размерности:. 2.3 Восприимчивость вещества. Так как зависимость намагничиваемости от нелинейна, то напишем уравнение для произвольной точки: . Для точки приведем коэффициент: . Тогда: , где безразмерная величина – восприимчивость вещества. 2.4 Абсолютная, относительная, дифференциальная магнитные проницаемости. Абсолютная магнитная проницаемость в точке – это соотношение: (это размерная величина). Относительная магнитная проницаемость: (это безразмерная величина). Абсолютная магнитная проницаемость определяется веществом. Основная кривая намагничивания (ОКН):
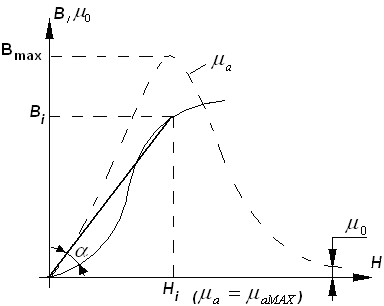
ОКН снимается для полностью размагниченного образца при медленном увеличении напряженности магнитного поля: - и так в каждой точке. Попробуем ответить на вопрос: как определить точку по графику ОКН, в которой?
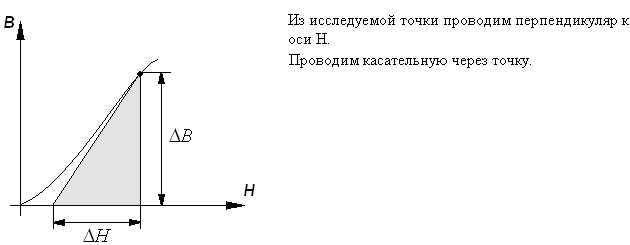
для нахождения точки с max магнитной проницаемостью необходимо провести прямую к этой точке через начало координат. Зависимость имеет очень большое значение для электромагнитных систем. График относительной магнитной проницаемости:
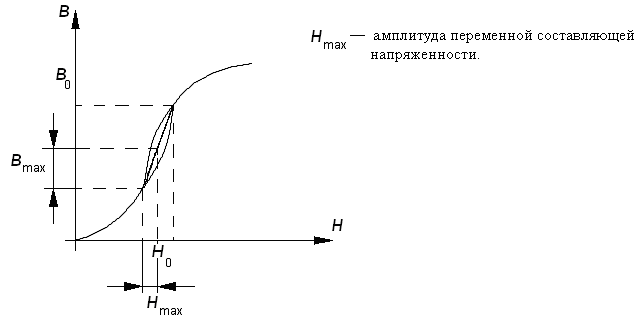
Дифференциальная магнитная проницаемость: Существует большое количество электромагнитных цепей, которые имеют постоянную и переменную составляющую (состоит из и ~).
Дифференциальная магнитная проницаемость определяется как скорость изменения ОКН в исследуемой точке.
Реакция магнитного вещества на действие магнитного поля. По реакции на действие магнитного поля магнитные вещества можно разделить на: парамагнитные; диамагнитные; ферромагнитные. Поведение магнитного вещества определяется двумя факторами: свойства вещества; действие температуры (увеличение температуры увеличивает кинетическую энергию атомов и молекул, что понижает эффективность воздействия магнитного поля). Для парамагнитных веществ магнитное поле элементарных токов взаимно и не компенсируется. Т.е. каждая частичка имеет свой магнитный момент. При отсутствии внешнего магнитного поля частица обладает магнитным моментом. При воздействии внешнего магнитного поля моменты частиц стремятся повернуться в направлении магнитного поля, немного усиливая его. Для парамагнитных веществ восприимчивость. К парамагнитным веществам относятся кислород и это его свойство используют для измерения концентрации кислорода. Повышение температуры приводит к уменьшению восприимчивости, т.к. линейно зависит от температуры. Диамагнитные вещества. Их атомы не обладают собственным магнитным моментом. При помещении диамагнитного вещества в магнитное поле, движение электронов по своим орбитам происходит без потери энергии (похоже на сверхпроводимость), следовательно, с атомами связан магнитный поток, который может быть изменен. Если поместить такое вещество в магнитное поле, то изменится скорость движения электронов таким образом, чтобы скомпенсировать поток, который стремиться проникнуть в объем, занимаемый атомами.
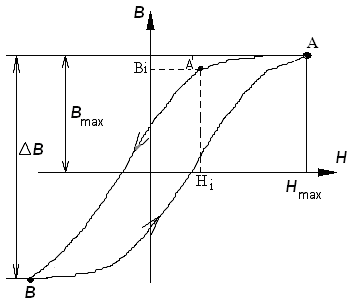
Диамагнитный эффект наиболее сильно проявляется у висмута. У него. Ферромагнитные вещества. При увеличении температуры домены, в большей или меньшей степени, разрушаются. При некоторой температуре ТК (точка Кюри) ферромагнитные вещества (их домены) разрушаются, и они становятся диамагнетиками. ТК (железа) = 770 оС; ТК (никеля) = 370 оС; ТК (кобальта) = 1200 оС. 2.6 Удельные потери на перемагничивание Вычислим работу, затрачиваемую при перемагничивании по петле Гистерезиса за цикл:
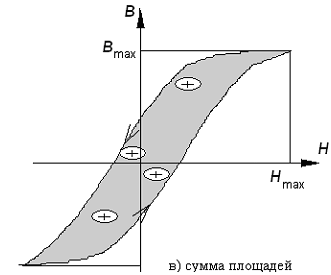
Работа внешнего источника за время:, где ток; ЭДС. С учетом закона электромагнитной индукции (, где потокосцепление): , где число витков. Вычислим работу на единицу объема: , где объем; длина образца; площадь сечения. (1) По закону полного тока: Если предположить, что: . Формулу (1) переписываем в виде: . Откуда потери на единицу объема за один цикл перемагничивания: , где петля динамического цикла.
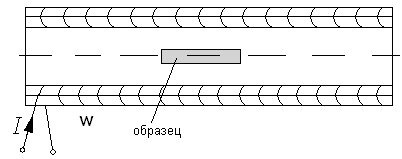
Выводы: 1. удельные потери, т.е. потери на единицу объема за один цикл перемагничивания равны площади петли динамического цикла. 2. удельные потери зависят от: свойства материала; частоты перемагничивания. Увеличение потерь на перемагничивание на переменном токе объясняется потерями на вихревые токи, которые возникают в «теле» образца и приводят к его нагреванию. для уменьшения потерь на перемагничивание магнитопровод выполняют в виде пластин, изолированных друг от друга. площадь динамического цикла увеличивается и при дальнейшем увеличении частоты намагничивания форма динамического цикла приближается к форме эллипса. 3 Испытание магнитомягких материалов на постоянном токе. Импульсно-индукционный метод измерения. Импульсно-индукционный метод измерения заключается в измерении индукции при импульсном изменении напряженности образца. 3.1 Общие сведения. Напряженность в кольцевом образце устанавливается по силе тока в намагничивающей обмотке с числом витков, равным.
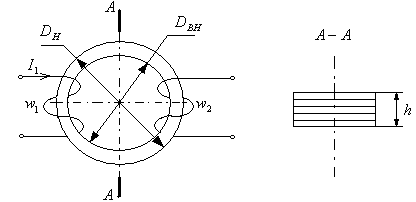
На рисунке обозначено: число витков измерительной обмотки; внутренний диаметр образца; наружный диаметр образца; образца. Образец набирается из колец. Подготовка образца к испытанию: на образец наносится изоляция; наносится намагничивающая обмотка (равномерно по кольцу образца); наносится изоляция; иногда наносится экран (экранируется измерительная обмотка); равномерно наносится намагничивающая обмотка. В соответствии с законом полного тока:, где длина контура интегрирования, который выбираем в виде окружности. будет зависеть от потому что. В соответствии с этим законом максимальная напряженность материале, расположенном ближе к. При увеличении длины контура интегрирования () уменьшается и достигает минимума вблизи. Выводы: 1. для любой длины контура интегрирования () измеренные значения индукции будут усредненными. 2. чтобы разброс индукции в каждой точке был, как можно меньше, необходимо сделать кольцо как можно более узким или уменьшить разницу. Чаще всего выбирают следующее соответствие: . 3. для расчета принимаем длину контура интегрирования, равной длине окружности среднего диаметра: . Тогда: , расчетные данные. Значения напряженности не измеряются, а устанавливаются по току намагничивания. Коэффициент пропорциональности зависит от наружного и внутреннего диаметров образца. Индукция измеряется в соответствии с законом электромагнитной индукции: . Из этой формулы видно, что для измерения индукции необходим интегратор: , где вольт-секундная площадь импульса в обмотке. изменение индукции за время интегрирования.
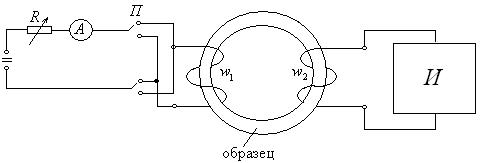
На рисунке обозначено: для измерения намагничивающего тока; переключатель для изменения полярности на обмотке; интегратор. 3.2 Основная кривая намагничивания (ОКН). Перед измерением образец размагничивается на переменном токе убывающей амплитуды, начиная со значения, соответствующего напряженности насыщения.
где изменение индукции при изменении напряженности от значения до значения; . Методика определения ОКН.
Рисунок 1. для переключения полярности намагничивающего тока (или, или), где - ток, соответствующий,; - ток в исследуемой точке (при,); диапазон измерения от десятков кОм до единиц Ом; пределы измерения от единиц мА до единиц А. Пояснение к рисунку: в замкнутом положении К устанавливается максимальное положение тока, которое устанавливается сопротивлением. Перед включением источника питания устанавливаются две точки: К – разомкнут; П – в положении 1; ; ; пределы устанавливают максимальными; вычисляют силу намагничивания тока по заданной напряженности: . выбираем предел измерения; включаем источник и устанавливаем значение, равное расчетному значению, не переходя этого значения. При этом изменяется значение; (Магнитная подготовка) в конце переключатель оставляем в положении 1. включаем и изменяем положение переключателя. Показания интегратора: , где показания образца. тогда: . по результатам измерений можно построить следующие зависимости: 3.3 Определение параметров петли магнитного гистерезиса.
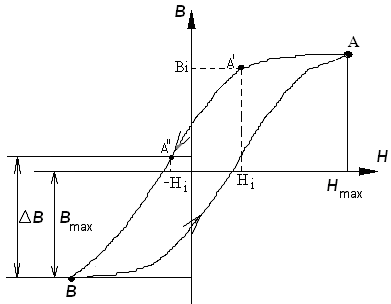
2) измерение всегда начинается в т.А и заканчивается в т.В. 3) перед измерениями необходимо знать и. Этими параметрами определяется петля динамического цикла. Для определения по заданной необходимо измерить это по методике определения ОКН. 3.3.1 Первый квадрант.
1 перед включением источника питания: замыкаем ключ К (рисунок 1); определяем для заданного значения:; устанавливаем предел максимального измерения амперметра и устанавливаем максимальные значения сопротивлений; включаем источник питания; по значению выбираем предел измерения; изменяя (уменьшая) значение, устанавливаем по амперметру значение. Этим самым устанавливается значение. При этом состояние образца – т.А. для заданного значения определяем ток, соответствующий: ; размыкаем ключ К; выбираем предел для тока; уменьшая значение, устанавливаем по амперметру значение; замыкаем ключ; магнитная подготовка: 10 раз коммутируем ключ К (из положения 1 в положение 2) и оставляем его в положении 1; замыкаем К; одновременно замыкаем К, включаем интегратор (И) и П переводим в положение «. При этом магнитное состояние образца перейдет из т. в т.В. При этом интегратор покажет значение магнитного потока, пропорционального изменению индукции: , где показания интегратора (вольт-секундная площадь обмотки). 3.3.2 Второй и третий квадранты.
по формуле , где модуль значения напряженности в исследуемой точке; замыкаем К, П – в положение 1. Магнитное состояние – т.А; выбираем предел измерения, устанавливая, равное. Размыкаем К; изменяя, устанавливаем ток. Магнитное состояние образца - т.; замыкаем К, тогда магнитное состояние – т.А; магнитная подготовка: оставляем П в положении 1; размыкаем К. Магнитное состояние - т.; не включая интегратор (И), размыкаем К. Магнитное состояние - т.; включаем интегратор (И) и размыкаем К. Магнитное состояние – т.В. Интегратор покажет з
|



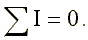
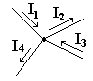 Токам, направленным к узлу, присвоим знак "плюс", а токам, направленным от узла - знак "минус". Получим следующее уравнение:
Токам, направленным к узлу, присвоим знак "плюс", а токам, направленным от узла - знак "минус". Получим следующее уравнение: или
или 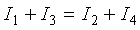
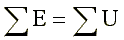
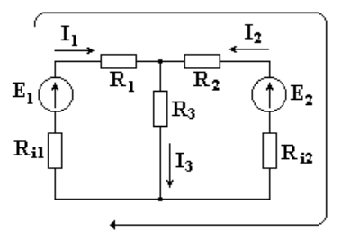 Для этого выберем произвольно направление обхода контура, например, по часовой стрелке. ЭДС и падения напряжений записываются в левую и правую части уравнения со знаком "плюс", если направления их совпадают с направлением обхода контура, и со знаком "минус", если не совпадают.
Для этого выберем произвольно направление обхода контура, например, по часовой стрелке. ЭДС и падения напряжений записываются в левую и правую части уравнения со знаком "плюс", если направления их совпадают с направлением обхода контура, и со знаком "минус", если не совпадают.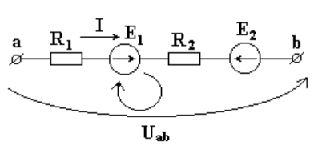 Возьмем замкнутый контур, состоящий из активной ветви и стрелки напряжения Uab, и запишем для него уравнение по второму закону Кирхгофа. Выберем направление обхода контура по часовой стрелке.
Возьмем замкнутый контур, состоящий из активной ветви и стрелки напряжения Uab, и запишем для него уравнение по второму закону Кирхгофа. Выберем направление обхода контура по часовой стрелке.

 ,
,


 .
.
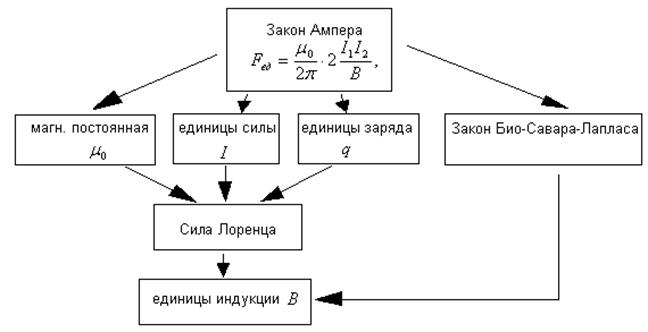

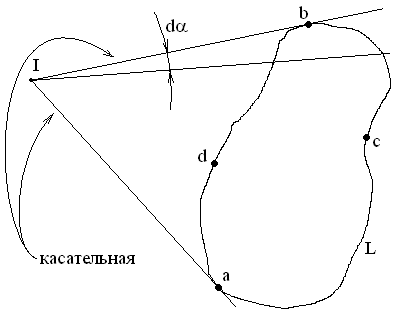

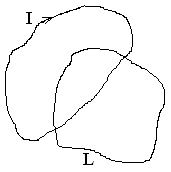
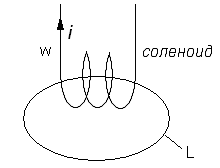
 рис. 1
рис. 1



 Таким образом, внешнее магнитное поле уменьшается и.
Таким образом, внешнее магнитное поле уменьшается и.




 1) измеряются параметры только одной ветви:. Т.е. подразумевается, что петля симметрична. Вторую часть петли можно достроить, используя принцип центральной симметрии.
1) измеряются параметры только одной ветви:. Т.е. подразумевается, что петля симметрична. Вторую часть петли можно достроить, используя принцип центральной симметрии.