Решение задачи

Установим характер влияния составляющих звеньев на замыкающее звено, то есть определим увеличивающие и уменьшающие звенья.

Звенья РЦ	Характер влияния на замыкающее звено
А1	Уменьшающее
А2	Уменьшающее
А3	Увеличивающее
А4	Не влияет
А5	Не влияет

А₁ и А₂ являются уменьшающими звеньями, так как при увеличении каждого из них при неизменных остальных составляющих звеньях замыкающее звено уменьшается. А при увеличении звена А₃ и при неизменных остальных звеньях замыкающее звено увеличивается, следовательно, А₃- увеличивающее звено. Звенья А₄ и А₅ не оказывают влияния на замыкающее звено, поэтому не будут включены в расчетную схему размерной цепи (рис. 2).

Рис. 2. Линейная размерная цепь: расчетная схема РЦ

Так как нумерация звеньев не соответствует принятой в [1], то переходим от расчетной схемы А к схеме Б, она изображена на рис. 3.

Рис. 3. Расчетная схема Б РЦ

Способ одного квалитета основан на том, что на все составляющие звенья (разумеется, кроме компенсирующего, если такое звено будет введено в РЦ) назначают допуски одного квалитета. Данный квалитет установим по значению расчетного коэффициента точности, вычисляемому по формуле (значения , отвечающие размерам , находим в табл. 1):

 

 

По полученному значению в табл. 1 выбираем ближайшее меньшее значение коэффициента точности и отвечающий этому значению 9 квалитет. Так как не совпадает ни с одним из табличных значений , то назначаем компенсирующее звено, роль которого будет выполнять увеличивающее звено .

Для размеров В₂ и В₃ допуски назначаем по 9-му квалитету:

мкм, мкм.

Их предельные отклонения

В₂=75_{-0,074 мм}, В₃= мм.

По формулам

определим координаты середин полей допусков звеньев , , :

 

мм;

мм;

мм.

 

Координату середины поля допуска компенсирующего звена В₁ , которое является увеличивающим, определим по формуле:

 

 

Допуск звена В₁ определим по формуле:

 

мм.

 

Теперь, по формулам определим верхнее и нижнее отклонения звена :

 

мм;

 

мм.

Следовательно,

 

мм.

 

Таким образом, звенья размерной цепи А в рамках решаемой задачи должны иметь следующие параметры:

мм;

мм;

мм;

мм.

 

Проверка. Считая предельные отклонения составляющих звеньев известными и равными тем, что установлены выше, определим допуск и предельные отклонения замыкающего звена. По характеру данная проверка относится к обратной задаче.

Допуск замыкающего звена определим по формуле:

 

мм.

 

Координату середины поля допуска замыкающего звена определим по формуле, при этом значения величин , , возьмем из решения прямой задачи:

 

мм.

 

Верхнее и нижнее отклонения замыкающего звена определим соответственно по формулам:

;

 

 

 

мм; (1)

 

мм. (2)

 

Сравнивая результаты проведенной проверки (1) и (2) с соответствующими исходными данными задачи

 

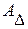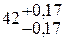= заключаем, что размерная цепь рассчитана правильно.