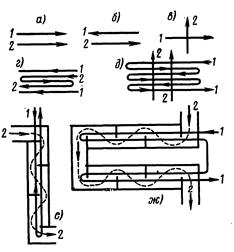
СХЕМЫ ДВИЖЕНИЯ ТЕПЛОНОСИТЕЛЕЙ И ТЕМПЕРАТУРНЫЙ НАПОР
Характер изменения температуры рабочих жидкостей вдоль поверхности нагрева зависит от схемы их движения и соотношения величин W 1 и W 2. Если в теплообменном аппарате горячая и холодная жидкости протекают параллельно и в одном направлении, то такая схема движения называется прямотоком (рис. 8-1, а). Если жидкости протекают параллельно, но в прямо противоположном направлении то такая схема называется противотоком (рис. 8-1, б). Схема взаимного движения, при которой жидкости протекают в перекрестном направлении называется перекрестным током (рис. 8-1, в). Помимо таких простых схем движения, на практике осуществляются и сложные: одновременно прямоток и противоток (рис. 8-1, г), многократно перекрестный ток, (рис. 8-1, д—ж) и т. д.
В зависимости от того, осуществляется ли прямоток или противоток и W 1 больше или меньше, чем W 2, получаются четыре характерные картины изменения температуры вдоль поверхности нагрева, представленные на рис. 8-2. Здесь по осям абсцисс отложена площадь поверхности нагрева F, а по осям ординат - температура рабочих жидкостей. В соответствии с уравнением (8-5) на графиках большее изменение температуры Из рассмотрения графиков следует, что при прямотоке конечная температура холодной жидкости При проведении расчетов возникает вопрос определения среднего температурного напора
Тепловой поток, передаваемый от горячей жидкости к холодной через элемент поверхности dF (рис. 8-3), определяется уравнением
При этом температура горячей жидкости понизится на
откуда
Изменение температурного напора при этом
где Подставляя в уравнение (д) значение dQ из уравнения (а), получаем:
Обозначим
Если значения m и k постоянны, то, интегрируя уравнение (ж), получаем:
или
откуда
где Из уравнения (и) видно, что вдоль поверхности нагрева температурный напор изменяется по экспоненциальному закону. Зная этот закон, легко установить и среднее значение температурного напора
Подставляя в уравнение (к) значение mkF и
или
Такое значение температурного напора называется среднелогарифмическим и часто в литературе обозначается Точно таким же образом выводится формула осреднения температурного напора и для противотока. Отличие лишь в том, что в правой части уравнения (г) следует поставить знак минус, и поэтому здесь
При равенстве величин W 1 и W 2 в случае противотока (m = 0) из уравнения (и) имеем:
Формулы (8-7) и (8-8) можно свести в одну, если независимо от начала и конца поверхности через
Вывод формул для среднелогарифмического температурного напора сделан в предположении, что расход и теплоемкость рабочих жидкостей, а также коэффициент теплопередачи вдоль поверхности нагрева остаются постоянными. Так как в действительности эти условия выполняются лишь приближенно, то и вычисленное по формулам (8-7), (8-8) или (8-9) значение В тех случаях, когда температура рабочих жидкостей вдоль поверхности нагрева изменяется незначительно, средний температурный напор можно вычислить как среднеарифметическое из крайних напоров
Среднеарифметическое значение температурного напора всегда больше среднелогарифмического. Но при Для аппаратов с перекрестным и смешанным током рабочих жидкостей задача об усреднении температурного напора отличается сложностью математических выкладок. Поэтому для наиболее часто встречающихся случаев результаты решения обычно представляются в виде графиков. Для ряда схем такие графики приведены в приложении. При помощи их расчет среднего температурного напора производится следующим образом. Сначала по формуле (8-8) определяется среднелогарифмический температурный напор как для чисто противоточных аппаратов. Затем вычисляются вспомогательные величины Р и R:
По этим данным из соответствующего вспомогательного графика (см. рис. П-5—П-15) находится поправка
6.6.3. АЛГОРИТМЫ ПРОЕКТИРОВОЧНОГО И ПОВЕРОЧНОГО РАСЧЕТОВ В принципе алгоритмы расчетов теплообменников могут быть построены по-разному и отличаться в зависимости от поставленной цели, вычислительных возможностей, требуемой точности расчетов и т.д. Ниже представлены упрощенные схемы расчетов, носящие в значительной степени иллюстративный характер. Реальные расчеты, особенно конструкторские, значительно более сложны, трудоемки и выполняются с использованием ЭВМ.
Рисунок 3.1 – Упрощенная схема-алгоритм теплового расчета ТОА Дать осреднение темпер напора
Конструкторский расчет. Укрупненная схема-алгоритм теплового расчета кожухотрубчатого охладителя показана на рис. 3.1. При этом считается, что заданы: конкретные холодный Т1 и горячий Т2 теплоносители; требуемые температуры теплоносителей на входе и выходе трубной полости:
В соответствии с исходными данными определяются средние температуры теплоносителей С использованием известного уравнения
определяется передаваемый в аппарате тепловой поток Q и требуемый массовый расход G 1 холодного теплоносителя. Другим основным расчетным уравнением является уравнение теплопередачи (8-3) Значение
где В случае использования других схем тока теплоносителей определение D t осуществляется с помощью зависимости (8-13). Коэффициент теплопередачи k учитывает процессы теплоотдачи с обоих сторон теплопередающей трубки и теплопроводности в самой трубке. Как правило, у труб, применяемых в теплообменниках d 2/ d 1 < 1,4. Поэтому с достаточной точностью зависимости для цилиндрических стенок можно заменить на зависимости для плоских стенок. Тогда:
Где: R 1 и R 2 - значения термических сопротивлений вследствие загрязнения поверхностей трубок.. Значения Скорости течения теплоносителя 1 в трубах задаются с использованием рекомендаций приложения Г. Если теплоноситель 1 – вода, а теплоноситель 2 – вязкая жидкость (масло), то задаваемые значения
Определяется общее количество труб n с учетом числа ходов Z 1. n=n*/Z1
Далее трубы компонуются в трубный пучок. Уточняется количество труб и достигаемые при этом Расчет
Далее определяют Расчет Найденные значения
Значения гидравлических сопротивлений D Р по каждому из трактов ТОА может быть найдено как сумма всех гидравлических сопротивлений по ходу течения теплоносителя и исполььзованием зависимостей, известных из гидродинамики:
Следует еще раз подчеркнуть, что приведенный упрощенный расчет является первым этапом проектирования ТОА, в ходе которого определяются его размеры и гидравлическое сопротивление. В дальнейшем, в зависимости от допустимых габаритов и гидравлического сопротивления, стараются изменить элементы конструкции и режимы течения теплоносителей (Z 1, Z 2, n,
Поверочный расчет. При проведении проектировочного расчета считается, что теплообменник уже имеется и целью теплового расчета является определение конечных температур рабочих жидкостей При решении такой задачи известными являются следующие величины: площадь поверхности нагрева F, коэффициент теплопередачи k, величины W 1 и W 2 и начальные температуры В приближенных расчетах можно исходить из следующих представлений. Количество теплоты, отдаваемое горячей жидкостью, равно:
откуда конечная температура ее
Соответственно для холодной жидкости имеем:
и
Если принять, что температуры рабочих жидкостей меняются по линейному закону, то
Вместо неизвестных
Произведя дальнейшее преобразование, получим:
откуда окончательно получаем:
Зная количество переданной теплоты Q, очень просто по формулам (а) и (б) определить и конечные температуры рабочих жидкостей Приведенная схема расчета хотя и проста, однако применима лишь для ориентировочных расчетов и в случае небольших изменений температур жидкостей.
Мощность, необходимая для прокачивания теплоносителей. Определив полное гидравлическое сопротивление и зная расход жидкости, легко определить и мощность, необходимую для перемещения рабочей жидкости через аппарат. Мощность на валу насоса или вентилятора определяется по формуле
где V — объемный расход жидкости; G — массовый расход жидкости; При выборе оптимальных форм и размеров поверхности нагрева теплообменника принимают наивыгоднейшее соотношение между поверхностью теплообмена и расходом энергии на движение теплоносителей. Добиваются, чтобы указанное соотношение было оптимальным, т. е. экономически наиболее выгодным. Это соотношение устанавливается на основе технико-экономических расчетов [37, 71, 79].
Из Бажана
|


 достигается для той жидкости, у которой значение величины W меньше.
достигается для той жидкости, у которой значение величины W меньше. всегда ниже конечной температуры горячей жидкости
всегда ниже конечной температуры горячей жидкости  . Таким образом, холодный теплоноситель в принципе не может быть прогрет до температуры выше температуры выходя горячего теплоносителя. При противотоке картина меняется. конечная температура холодной жидкости
. Таким образом, холодный теплоноситель в принципе не может быть прогрет до температуры выше температуры выходя горячего теплоносителя. При противотоке картина меняется. конечная температура холодной жидкости  в зависимости (8-3). При выводе формулы осреднения температурного напора рассмотрим простейший теплообменный аппарат, работающий по схеме прямотока.
в зависимости (8-3). При выводе формулы осреднения температурного напора рассмотрим простейший теплообменный аппарат, работающий по схеме прямотока.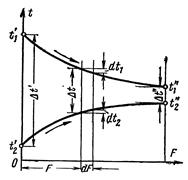
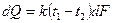 (а)
(а)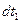 , a холодной повысится на
, a холодной повысится на 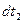 . Следовательно,
. Следовательно,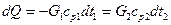 (б)
(б)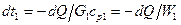 (в)
(в)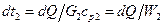 (г)
(г)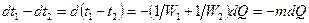 (д)
(д)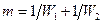 .
. (е)
(е)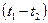 через
через 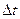 и произведем разделение переменных:
и произведем разделение переменных: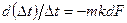 (ж)
(ж)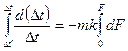
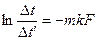 , (з)
, (з)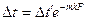 , (и)
, (и)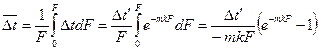 (к)
(к)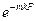 из уравнений (з) и (и) и имея в виду, что согласно рис. 8-3 в конце поверхности нагрева
из уравнений (з) и (и) и имея в виду, что согласно рис. 8-3 в конце поверхности нагрева 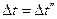 , окончательно имеем:
, окончательно имеем: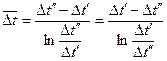 (8-7)
(8-7)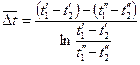 (8-7а)
(8-7а) .
.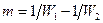 . Окончательная формула для среднего логарифмического температурного напора при противотоке имеет вид:
. Окончательная формула для среднего логарифмического температурного напора при противотоке имеет вид: (8-8)
(8-8) . В этом случае температурный напор по всей поверхности постоянен:
. В этом случае температурный напор по всей поверхности постоянен: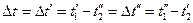 (л)
(л) обозначить больший, а через
обозначить больший, а через 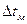 меньший температурные напоры между рабочими жидкостями. Тогда окончательная формула среднелогарифмического температурного напора для прямотока и противотока принимает вид:
меньший температурные напоры между рабочими жидкостями. Тогда окончательная формула среднелогарифмического температурного напора для прямотока и противотока принимает вид: (8-9)
(8-9)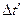 и
и 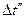 :
: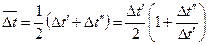 (8-10)
(8-10)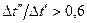 они отличаются друг от друга меньше чем на 3%. Такая погрешность в технических расчетах вполне допустима.
они отличаются друг от друга меньше чем на 3%. Такая погрешность в технических расчетах вполне допустима. ; (8-11)
; (8-11)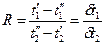 . (8-12)
. (8-12)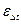 . Итак, в общем случае средний температурный напор определяется формулой
. Итак, в общем случае средний температурный напор определяется формулой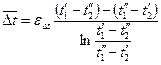 =
=  (8-13)
(8-13)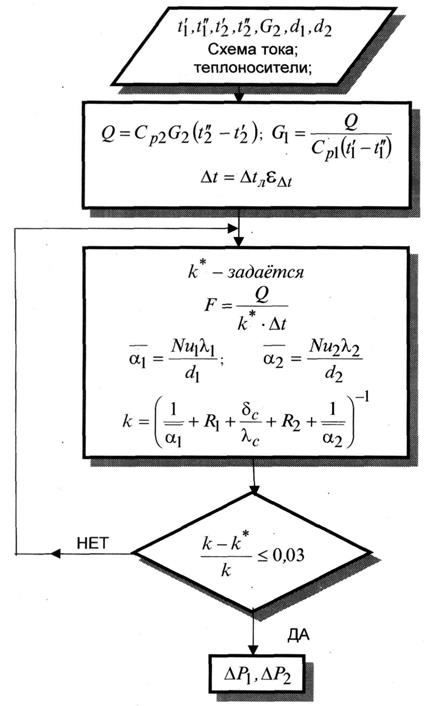
 и
и  , а также межтрубной полости
, а также межтрубной полости  и
и  ; массовый расход теплоносителя межтрубной полости
; массовый расход теплоносителя межтрубной полости 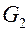 ; материал и внутренний
; материал и внутренний 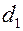 и наружный
и наружный 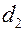 диаметры используемых труб трубного пучка; схема движения теплоносителей в теплообменнике и допустимые гидравлические сопротивления.
диаметры используемых труб трубного пучка; схема движения теплоносителей в теплообменнике и допустимые гидравлические сопротивления.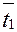
 и
и  . Обычно эти температуры являются определяющими при выборе теплофизических свойств теплоносителей.
. Обычно эти температуры являются определяющими при выборе теплофизических свойств теплоносителей.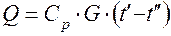 (3.1)
(3.1)
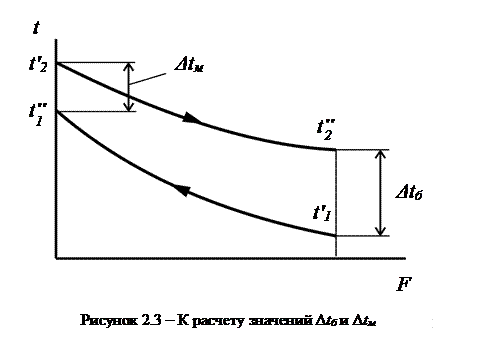
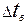 и
и 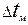 – соответственно наибольший и наименьший температурные напоры, независимо от начала и конца теплообменной поверхности (см. рис. 2.3).
– соответственно наибольший и наименьший температурные напоры, независимо от начала и конца теплообменной поверхности (см. рис. 2.3). .
. и
и 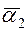 определяются по результатам расчетов, обычно с использование уравнений подобия.
определяются по результатам расчетов, обычно с использование уравнений подобия.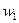 из приложения Г следует уменьшить примерно в 2…3 раза. Это объясняется тем, что определяющей будет теплоотдача теплоносителю 2 и нет особой необходимости обеспечивать высокие скорости
из приложения Г следует уменьшить примерно в 2…3 раза. Это объясняется тем, что определяющей будет теплоотдача теплоносителю 2 и нет особой необходимости обеспечивать высокие скорости 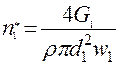 .
. требует знания F. Для этого задаются в первом приближении значением К * (см. приложение Е) и по уравнению (8-3) определяют F.
требует знания F. Для этого задаются в первом приближении значением К * (см. приложение Е) и по уравнению (8-3) определяют F.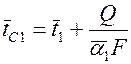
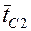 , задаются шагом труб в трубном пучке S, диаметром трубного пучка DТП, определяют внутренний диаметр корпуса D, требуемую длину l между трубными досками, количество ходов Z 2 в межтрубной полости, проходное сечение f 2 и скорость
, задаются шагом труб в трубном пучке S, диаметром трубного пучка DТП, определяют внутренний диаметр корпуса D, требуемую длину l между трубными досками, количество ходов Z 2 в межтрубной полости, проходное сечение f 2 и скорость  . Если достигнутая скорость
. Если достигнутая скорость  ведется по зависимостям, указанным в приложении 7.
ведется по зависимостям, указанным в приложении 7. ,
,  .
.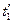 и
и 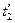 а искомыми: конечные температуры
а искомыми: конечные температуры 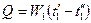 (8-16)
(8-16) (а)
(а)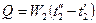 (8-17)
(8-17) (б)
(б)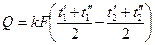 (в)
(в) (г)
(г) (д)
(д)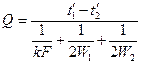 (8-18)
(8-18)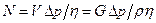 )
) — полное сопротивление;
— полное сопротивление; 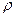 — плотность жидкости или газа;
— плотность жидкости или газа; 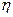 — к. п. д. насоса или вентилятора.
— к. п. д. насоса или вентилятора.


