Молекулярная диффузия
Молекулярная диффузия происходит в газах, жидкостях (при отсутствии конвективного движения), а также в твердых телах в результате хаотического движения молекул. Если в системе имеются области с высокой и низкой концентрациями какого-либо вещества, то при отсутствии противодействующих сил концентрации в указанных областях стремятся выровняться. Кинетика такого переноса вещества подчиняется 1-му закону Фика, аналогичному закону теплопроводности:
где dG – количество перенесенного вещества; ¶c/¶x – градиент концентрации в направлении диффузии; dF – площадь контакта фаз; dt - время диффузии; D – коэффициент диффузии. Коэффициент диффузии представляет собой физическую константу, характеризующую способность данного вещества проникать вследствие диффузии в неподвижную среду. Величина коэффициента диффузии не зависит от гидродинамических условий, в которых протекает процесс. Значения коэффициента диффузии являются функцией свойств распределяемого вещества, свойств среды, через которую оно диффундирует, температуры и давления. Величина коэффициента диффузии может быть определена по уравнению Эйнштейна:
где r – размер частиц распределяемого вещества; h - вязкость среды. Процесс молекулярной диффузии можно описать дифференциальным уравнением, составляющим 2-ой закон Фика:
Конвективная диффузия В движущейся среде перенос вещества осуществляется как молекулярной диффузией, так и самой средой в направлении ее движения или отдельными ее частицами в разнообразных направлениях. Закон конвективной диффузии, открытый Щукаревым, является аналогом закона теплоотдачи Ньютона. Его математическое выражение имеет вид:
где b - коэффициент массоотдачи, характеризующий перенос вещества одновременно диффузией и конвекцией; cr – концентрация распределяемого вещества на границе фазы и рассматриваемая, как равновесная; cf – концентрация в ядре потока. Распределение концентраций при переносе вещества путем конвективной диффузии определяется в самом общем виде дифференциальным уравнением конвективной диффузии, имеющим вид:
В данном уравнении помимо концентрации, переменной величиной является скорость потока w. Поэтому данное уравнение надо рассматривать совместно с дифференциальными уравнениями гидродинамики. Однако такая система уравнений не имеет аналитического решения, и для получения расчетных зависимостей дифференциальное уравнение конвективной диффузии преобразуют методами теории подобия.
|

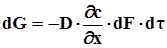 , (16)
, (16)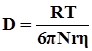 , (17)
, (17)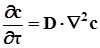 (18)
(18)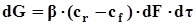 , (19)
, (19)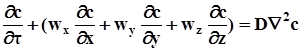 (20)
(20)


