Оператор размерности массива DIMENSION
Массивы в отличие от простых переменных требуют предварительного описания. Для этой цели в языке Бейсик служит оператор DIM, в котором указываются имена описываемых массивов и их максимальные индексы. Например, оператор DIM M(10), N%(99) резервирует область памяти под массив М, предназначенный для хранения одиннадцати вещественных значений (индексы массива обычно пробегают значения от 0 до максимального) и область под массив N% для хранения ста целых чисел. Для описания многомерных массивов необходимо после имени массива в скобках указывать несколько максимальных значений индексов (по числу измерений). Например, оператор DIM К#(19,4) резервирует место под двумерный массив вещественных чисел, представленных в памяти с двойной точностью. Общий вид оператора DIM: DIM <имя массива> (<размерность>) Описание массива, если оно есть, должно быть произведено до первого обращения к его элементам. При этом в большинстве версий языка максимальное значение индекса может быть задано произвольным арифметическим выражением. Это означает, что допускается переменный размер массива. В отличие от языка Паскаль, где массивы описываются только статически (т. е. размеры массивов должны быть известныдо начала выполнения программы), в Бейсик-программе возможно, например, такое задание размера массива: INPUT L DIM M(L) Если массив предварительно не описан в программе, то по умолчанию ему приписывается по всем измерениям максимальный индекс, равный 10. Обращение к компонентам массива производится через переменные с индексами, которые представляют собой последовательность из имени массива и в круглых скобках перечисленных через запятую индексов по числу измерений. Например, М(0) — обращение к первому компоненту массива М, а К# (2,4) — обращение к элементу вещественного с двойной точностью массива, стоящему на пересечении третьей строки и пятого столбца. Рассмотрим задачу, в которой надо ввести массив чисел, найти в нем максимальное число, все элементы массива, стоящие на четных местах, увеличить на абсолютную величину этого максимального числа и распечатать измененный массив: REM ПРИМЕР INPUT "ВВОДИ КОЛИЧЕСТВО ЧИСЕЛ В МАССИВЕ->";N DIM M(N) REM ВВОД ЭЛЕМЕНТОВ МАССИВА FOR I=l TO N INPUT "ВВОДИ ЧИСЛО->";М(I) NEXT I REM ПОИСК МАКСИМАЛЬНОГО ЭЛЕМЕНТА MAX=M(l) FOR I=2 TO N IF M(I)>= MAX THEN MAX=M(I) NEXT I PRINT "МАКСИМАЛЬНОЕ ЧИСЛО В МАССИВЕ -"; MAX REM ИЗМЕНЕНИЕ ЭЛЕМЕНТОВ ИСХОДНОГО МАССИВА FOR I=2 ТО N STEP 2 M(I)=M(I)+ABS(MAX) NEXT I REM ВЫВОД ЭЛЕМЕНТОВ ПОЛУЧЕННОГО МАССИВА FOR I=l TO N PRINT M(I); NEXT I END Надо отметить, что мы зарезервировали под массив область памяти большую, чем требовалось для хранения вводимых чисел. В программе не использовался элемент массива с нулевым индексом, так как привычнее нумеровать элементы с единицы. Зарезервированное место в памяти было потрачено впустую. Для одномерных массивов это не существенно, а для больших многомерных массивов приводит к потере немалых емкостей оперативной памяти, которая уже не может быть использована для размещения полезной информации при выполнении данной программы. В большинстве систем имеется специальный оператор OPTION BASE, позволяющий изменять устанавливаемое по умолчанию начальное значение индекса. Этот оператор должен выполняться в программе до первого оператора, содержащего имена массивов, включая DEF и DIM. Общий вид оператора: OPTION BASE К
Величина К может принимать значение 0 или 1. В соответствии со значением К оператор устанавливает начальное значение индекса для всех массивов программы равным О или 1. В нашей программе оператор OPTION BASE 1 уменьшил бы емкость памяти, резервируемую оператором DIM M(N), с (N+1) до N ячеек, а, например, для двумерного массива А (10,10) — со 121 до 100 ячеек памяти. Термин "ячейка" здесь употреблен условно, как место в памяти, выделенное для хранения одного элемента массива. В приведенной программе ввод и вывод элементов массива М организован с помощью операторов цикла FOR— NEXT. В первом цикле элементы исходного массива чисел вводятся пользователем с терминала, при этом каждое значение набирается с новой строки. В последнем цикле программы элементы измененного массива выводятся на экран в одну строку, так как оператор PRINT заканчивается точкой с запятой, и курсор не переводится на новую строку после вывода очередного значения. Для ввода и вывода значений многомерных массивов обычно используются вложенные циклы. Например, следующий фрагмент программы вводит построчно значения двумерного массива: DIM Y(3,5) FOR I=1 TO 3 FOR J=1 TO 5 INPUT Y(I,J) NEXT J NEXT I Приведенный ниже фрагмент программы выводит построчно значения элементов этого массива: FOR I=l TO 3 FOR J=l TO 5 PRINT Y(I,J); NEXT J NEXT I Оператор PRINT обеспечивает печать с новой строки при переходе к выводу элементов очередной строки матрицы. Пример 1. Вычислить среднее арифметическое четных чисел одномерного массива А(I), I=1,N, стоящих на нечетных позициях. INPUT "ВВЕДИТЕ РАЗМЕРНОСТЬ МАССИВА";N DIM A(N) FOR I=1 TO N PRINT "A(";I;")="; INPUT A(I) NEXT I S=0 K=0 FOR I=1 TO N STEP 2 IF A(I)/2=INT(A(I)/2) THEN S=S+A(I) K=K+1 END IF NEXT I PRINT "СРЕДНЕЕ АРИФМЕТИЧЕСКОЕ = "; S/K END Пример 2. В одномерном массиве A(I), I=1,N определить количество отрицательных элементов и на их место записать нули. При отсутствии отрицательных элементов на экран дисплея вывести сообщение: "Отрицательных элементов нет" INPUT "Введите количество элементов в массиве";N DIM A(N) FOR I = 1 TO N INPUT A(I) NEXT I k = 0 FOR I = 1 TO N IF A(I) < 0 THEN k = k + 1 A(I) = 0 END IF NEXT I IF k = 0 THEN PRINT "Отрицательных элементов нет" ELSE PRINT "Количество отрицательных элементов="; k PRINT "Полученный массив:" FOR I = 1 TO N PRINT A(I); NEXT I END IF END Пример 3. Из числового массива A(I), I=1,N образовать массив B(I), I=1,N, в котором сначала расположены нулевые элементы массива, а затем положительные и отрицательные. INPUT "Введите размерность массива";N DIM A(N), B(N) FOR I = 1 TO N INPUT A(I) NEXT I J = 0 FOR I = 1 TO N IF A(I) = 0 THEN J = J + 1 B(J) = A(I) END IF NEXT I FOR I = 1 TO N IF A(I) > 0 THEN J = J + 1 B(J) = A(I) END IF NEXT I FOR I = 1 TO N IF A(I) < 0 THEN J = J + 1 B(J) = A(I) END IF NEXT I FOR I = 1 TO N PRINT B(I); NEXT I END Пример 4. Имеется два массива действительных чисел A(I) и B(I), I=1,16. Составить последовательность Z по правилу: Z1=A1×B2; Z2=A2×B4; Z3=A3×B6;…; Z8=A8×B16. В полученном массиве найти суммы трех первых и трех последних элементов. INPUT "N="; N DIM A(N), B(N), Z(N/2) FOR I = 1 TO N PRINT "Введите A("; I; "), B("; I; ")" INPUT A(I), B(I) NEXT I FOR I = 1 TO N/2 Z(I) = A(I) * B(I * 2) PRINT Z(I); NEXT I S1 = 0: S2=0 FOR I = 1 TO 3 S1 = S1 + Z(I) NEXT I FOR I = N/2 TO N/2-2 STEP -1 S2 = S2 + Z(I) NEXT I PRINT "S1="; S1 PRINT "S2="; S2 END Пример 5. Составить программу поиска в двумерном массиве A(I,J), I=1,N; J=1,M наибольшего и наименьшего элементов массива и их индексов. INPUT "Введите N=,M="; N, M DIM A(N, M) FOR I = 1 TO N FOR J = 1 TO M PRINT " A("; I; J; ")="; INPUT A(I, J) NEXT J, I MAX = A(1, 1) STMAX = 1 SBMAX = 1 MIN = MAX STMIN = 1 SBMIN = 1 FOR I = 1 TO N FOR J = 1 TO M IF A(I, J) > MAX THEN MAX = A(I, J) STMAX = I SBMAX = J ELSEIF A(I, J) < MIN THEN MIN = A(I, J) STMIN = I SBMIN = J END IF NEXT J, I PRINT "Максимальный элемент и его индексы="; MAX; STMAX; SBMAX PRINT "Минимальный элемент и его индексы="; MIN; STMIN; SBMIN END Пример 6. Для каждой строки заданной матрицы A(I,J), I=1,N; J=1,M определить сумму элементов, кратных 3, среди полученных значений определить минимальное и количество чисел равных ему. INPUT "N=,M="; N, M DIM A(N, M), S(N) FOR I = 1 TO N FOR J = 1 TO M PRINT " A("; I; J; ")="; INPUT A(I, J) NEXT J, I FOR I = 1 TO N S(I) = 0 FOR J = 1 TO M IF A(I, J) MOD 3 = 0 THEN PRINT "A="; A(I, J) S(I) = S(I) + A(I, J) END IF NEXT J, I MIN = S(1) FOR I = 1 TO N IF S(I) < MIN THEN MIN = S(I) END IF NEXT I K = 0 FOR I = 1 TO N IF S(I) = MIN THEN K = K + 1 END IF NEXT I PRINT "MIN="; MIN; "Kоличество чисел, равных ему="; K END Пример 7. Для заданной квадратной матрицы определить сумму элементов, стоящих на главной диагонали и произведение элементов, стоящих на побочной диагонали. INPUT "Введите размерность матрицы N="; N DIM A(N, N) FOR I = 1 TO N FOR J = 1 TO N PRINT " A("; I; J; ")="; INPUT A(I, J) NEXT J, I S = 0 FOR I = 1 TO N S = S + A(I, I) NEXT I P = 1 FOR I = 1 TO N FOR J = 1 TO N IF I + J = N + 1 THEN P = P * A(I, J) END IF NEXT J, I PRINT "S = "; S; " P = "; P; END Пример 8. С помощью функции
INPUT "Введите размерность матрицы ";N DIM A(N, N), X(N) PRINT "Создание матрицы–›" I = 1 DO WHILE I <= N J = 1 DO WHILE J <= N A(I, J) = 2 * (J / 2 - 3.1) * (-2) ^ I * (I - 4) J = J + 1 LOOP I = I + 1 LOOP PRINT "Нахождение максимального элемента" MAX = A(1, 1) I = 1 DO WHILE I <= N J = 1 DO WHILE J <= N IF A(I, J) > MAX THEN MAX = A(I, J) NST = I NSB = J END IF J = J + 1 LOOP I = I + 1 LOOP PRINT "Построение вектора" I = 1 DO WHILE I <= N X(I) = A(NST, I) * A(I, NSB) I = I + 1 LOOP PRINT "Печать вектора" I = 1 DO WHILE I <= N PRINT X(I); I = I + 1 LOOP END
|

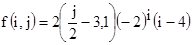 создать матрицу A(i,j), i=1,n; j=1,n. Построить вектор Х элементы которого равны скалярному произведению строки на столбец, на пересечении которых находится максимальный элемент матрицы А.
создать матрицу A(i,j), i=1,n; j=1,n. Построить вектор Х элементы которого равны скалярному произведению строки на столбец, на пересечении которых находится максимальный элемент матрицы А.


