Представление связи в сети в матричной форме.
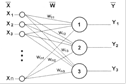
Рассмотрим нейронные сети, у которых нет обратных связей, то есть соединений, идущих от выходов некоторого слоя к входам этого же слоя или предшест-вующих слоев. Этот специальный класс сетей, называемых сетями без обратных связей или сетями прямого распространения, представляет интерес и широко используется. Простейшая однослойная сеть прямого распространения, состоящая из группы нейронов, показана на рис. 2.18.
Рис. 2.18. Однослойная НС На п входов поступают некие сигналы, проходящие по синапсам на 3 нейрона, образующие единственный слой этой НС и выдающие три выходных сигнала:
где j = 1, 2, 3. В искусственных и естественных (биологических) сетях многие соединения могут отсутствовать, все соединения показаны в целях общности. Очевидно, что все весовые коэффициенты синапсов одного слоя нейронов можно свести в матрицу W, в которой каждый элемент wij задает величину i -й синаптической связи j -го нейрона. Таким образом процесс, происходящий в НС, может быть записан в матричной форме: Y = F (XW) где X и Y – соответственно входной и выходной сигнальные векторы; F (V) – активационная функция, применяемая поэлементно к компонентам вектора V. На рис. 2.19 представлена двухслойная НС, полученная из однослойной (см. рис. 2.18) путем добавления второго слоя, состоящего из двух нейронов. Здесь уместно отметить важность роли рассмотренной ранее нелинейности активационпой функции, так как, если бы она не обладала данным свойством или не входила в алгоритм работы каждого нейрона, результат функционирования любой р-слойной НС с весовыми матрицами W (i), где i =1,2,…, p для каждого слоя i сводился бы к перемножению входного вектора сигналов Х на матрицу W (Σ) = W (1) W (2)… W (р) то есть фактически такая р-слойная НС эквивалентна однослойной НС с весовой матрицей единственного слоя W(Σ): Y = XW (Σ).
Рис. 2.19. Двухслойная НС Таким образом, для расширения вычислительных возможностей многослойных НС по сравнению с однослойными НС необходимо использование нелинейных активационных функций. Продолжая разговор о нелинейности, необходимо отметить, что она иногда может вводиться и в синаптические связи. В большинстве известных на сегодняшний день НС для нахождения взвешенной суммы входов нейрона используют формулу Несколько слов необходимо сказать о требуемой мощности выходного слоя сети, выполняющего окончательную классификацию пространства состояний. Дело в том, что для разделения множества входных образов, например, по двум классам достаточно всего одного выхода. При этом каждый логический уровень – «1» и «0» – будет обозначать отдельный класс. На двух выходах можно закодировать уже четыре класса и т. д.
|

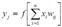

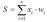 , однако в некоторых приложениях НС полезно ввести другую запись, например:
, однако в некоторых приложениях НС полезно ввести другую запись, например: 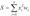 или
или  .
.


