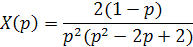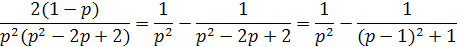Соответствие между оригиналами и изображениями
Таблица 2
Пример 1. Дана струна, закрепленная на концах х =0 и х = l. Пусть в начальный момент форма струны имеет вид ломаной ОАВ (рисунок 1). Найти форму струны для любого времени t, если начальные скорости отсутствуют.
Прямая АВ отсекает на осях координат отрезки l и 2 h, поэтому уравнение этой прямой имеет вид х/l+u/(2h)=l, или u =(2 h / l)(l - x). Итак,
Следовательно,
Выпишем несколько членов ряда:
Пример 2. Вычислить интеграл а) отрезок прямой от точки 0 до точки 1+2 i; б) дуга параболы y=2x2 от точки 0 до точки 1+2 i. Решение. Так как l - отрезок прямой y =2 x (рис. 2) и Imz = y, то
Так как для всех точек l имеем y=2x2, то (рис. 3)
Пример 3. Найти оригинал x (t) по заданному изображению X (p), где
Решение. Разложим дробь на простейшие дроби:
Поэтому
Перейдем от изображений к оригиналам, используя таблицу 2:
Пример 4. Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям: x //-2 x /+2 x =2 t -2, x (0)= x /(0)=0. Решение. Пусть x (t) x/ (t) x //(t) Так как то приходим к операторному уравнению
из которого находим изображение X (p) частного решения дифференциального уравнения:
Методом неопределенных коэффициентов находим разложение этой дроби в виде суммы дробей, являющихся оригиналами элементарных функций:
Следовательно, Контрольная работа по теме: ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ.
3.Найти решение задачи Коши.
|

 (оригинал)
(оригинал)
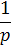
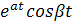


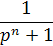
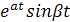

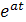
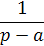

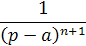

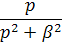
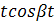
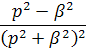

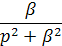
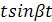
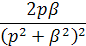
 Решение. Угловой коэффициент ОА (рис.1) равен h /(l /2), т.е. 2 h / l. Следовательно, уравнение этой пря мой есть u =(2 h / l) x.
Решение. Угловой коэффициент ОА (рис.1) равен h /(l /2), т.е. 2 h / l. Следовательно, уравнение этой пря мой есть u =(2 h / l) x.
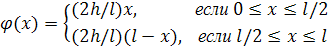
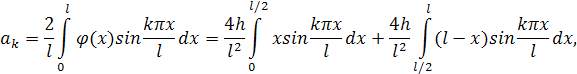
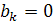 . Интегрируя по частям, получаем:
. Интегрируя по частям, получаем: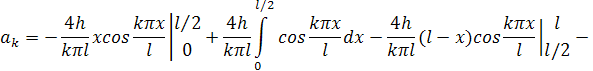


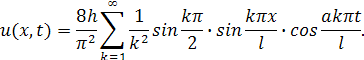
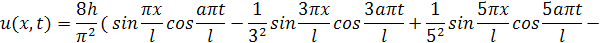
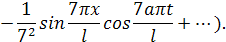
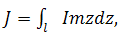 где l:
где l: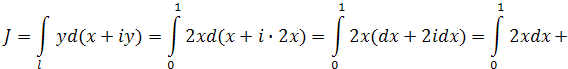
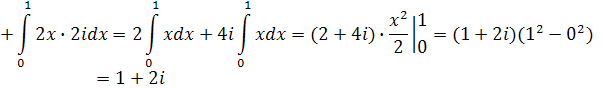





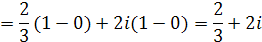
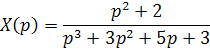
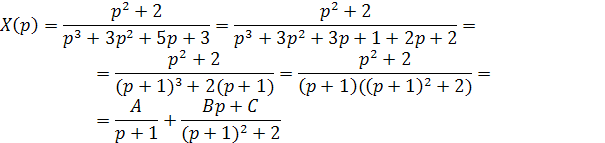
 Полагая в этом тождестве последовательно р =-1, р =0 и приравнивая коэффициенты при р 2, находим: 2 А =3; 3 А + С =2; А + В =1, откуда A =3/2, B =-1/2, C =1/2.Таким образом, получаем:
Полагая в этом тождестве последовательно р =-1, р =0 и приравнивая коэффициенты при р 2, находим: 2 А =3; 3 А + С =2; А + В =1, откуда A =3/2, B =-1/2, C =1/2.Таким образом, получаем:
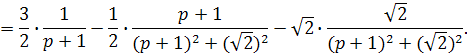
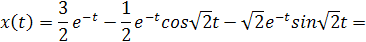

 X (p). По теореме о дифференцировании оригинала получаем изображения производных функции x (t):
X (p). По теореме о дифференцировании оригинала получаем изображения производных функции x (t):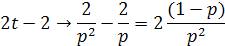 ,
,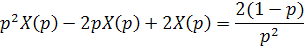 ,
,