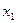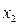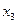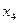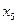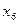СЕМЕСТРОВОЕ ЗАДАНИЕ

по дисциплине «Дискретная математика»

 

 

Выполнила: студентка группы ММ-233

Молодорич М.И..

Дата «___» «»2010 г.

Проверил

Никитин Г.А.

Дата «___» «»2010 г.

 

 

Челябинск 2010

 

Содержание.

 

Постановка задачи. 3

Метод Квайна. 5

Карты Карно. 15

Метод кубических покрытий. 23

Анализ результатов. 63

 

Постановка задачи.

Дана функция шести переменных Y=(4)v(6)v(10)v(16)v(23)v(25)v(30)v (32)v(37)v(51)v(62)v(67)v0v1v2v3v14v17v22v24v26v27v31v33v35v36v40v41v42v43v50v54v55v56v60v61v63v65v66v70v71v73v74v75v76v77. Числа заданы в восмеричной системе счисления, на наборах хх функция принимает значение 1, на наборах (хх) не определена.

1. Доопределить функцию нулями и минимизировать полученную функцию методом Квайна.
2. Доопределить функцию единицами и минимизировать полученную функцию с помощью карт Карно.
3. Минимизировать исходную функцию с использованием метода кубических покрытий. Минимальное покрытие ищется для недоопределенной функции, доопределение произведется в ходе вычислений.
4. Построить таблицу истинности исходной и полученных функций. Проанализировать таблицу. Сделать выводы относительно методов и полученных минимальных форм. Сравнить полученные минимальные формы по цене.

Таблица истинности исходной функции.

№

Значение

№

Значение

Не опред.

Не опред.

Не опред.

Не опред.

Не опред.

Не опред.

Не опред.

Не опред.

Не опред.

Не опред.

Не опред.

Не опред.

Метод Квайна.

Исходным является множество конституент единицы функции.

Запишем в таблицу все конституенты единицы функции. Выполним все возможные операции неполного попарного склеивания.Выполним все возможные операции элементарного поглощения.Все импликанты, участвовавшие в поглощении, отметим в таблице знаком ‘+’. Те импликанты, которые не участвовали в поглащении, войдут в СкДНФ. На каждом следующем этапе будем выполнять те же действия для множества импликант, полученных в результате неполного попарного склеивания на предыдущем этапе. Алгоритм завершается, когда данное множество является пустым, либо нельзя выполнить ни одной операции неполного попарного склеивания.

Для нахождения МДНФ построим таблицу, в которой будем отмечать, какие единицы функции покрывает каждая из простых импликант. Найдем все единицы функции, которые покрываются только одной импликантой системы. Эти импликанты образуют ядро функции, отметим найденные единицы и импликанты знаком ‘ü’. Все не помеченные единицы, покрытые ядром, отметим знаком ‘-’. Выпишем оставшиеся единицы и импликанты системы в новую таблицу. Произведем упорядочивание: если одинаковые наборы единиц покрываются двумя импликантами разной длины, то удаляем импликанту большей длины; если первая импликанта покрывает те же единицы, что и вторая, плюс еще какие-то, то удаляем вторую импликанту.На каждом следующем этапе будем повторять те же действия для оставшихся импликант и единиц функции, получая псевдоядро, пока не будут покрыты все единицы функции. Ядро и псевдоядра образуют МДНФ.

Возможно, что на каком-то шаге не найдется ни одной единицы функции, которая покрывается одной импликантой. В этом случае ищется наилучшее покрытие оставшихся единиц функции методом перебора.