Карты Карно. 1 страница
Построим карты Карно и выделим все компактные группы наибольшей размерности, покрывающие р-клетки.
Получаем 12 компактных групп размерности 3 и 17 компактных групп размерности 2. Соответствующие им импликанты образуют сокращенную дизъюнктивную нормальную форму. СкДНФ:
Найдем р-клетки, покрытые только одной компактной группой; импликанты, соответствующие этой компактной группе, образуют ядро функции (в смысле Квайне). Отметим цветом все р-клетки, покрытые ядром функции (белые единицы – покрытые одной компактной группой, серые клетки – покрытые). На каждом следующем шаге будем рассматривать оставшиеся непокрытыми р-клетки. Делаем упорядочивание, т.е. удаляем из рассмотрения первую компактную группу, если она покрывает те же р-клетки, что и вторая компактная группа, но вторая компактная группа покрывает больше непокрытых клеток. Снова находим р-клетки, покрытые только одной компактной группой(если таких клеток нет, то производится ветвление: выбираем какую-либо импликанту и смотрим цена какой ТДНФ будет меньше с данной импликантой или без); импликанты, соответствующие этим компактным группам, входят в псевдоядро функции. Так повторяем, пока все р-клетки не окажутся покрытыми.
Ядро функции: {
Упорядочивая перебор, удаляем из рассмотрения {
Псевдоядро: { Пусть импликанта
Псевдоядро: { Упорядочивая перебор, удаляем из рассмотрения { Пусть импликанта
|

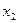
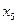
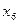 v
v 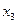
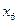 v
v 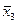
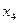
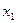
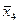 v
v 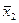
 v
v 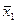
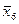 v
v 


