Частные производные и полный дифференциал функции нескольких переменных.
Рассмотрим y=(x), x ⊂ R, y ⊂R; px (x,x₀)= (x-x₀) py (y, y₀)=(y-y₀) Число Если Предел функции нескольких переменных. Пусть задана функция z=f (x,y). Если Пусть функция двух переменных z=f(x;у) (для большего количества переменных всё аналогично) определена в некоторой окрестности точки М (x;у). Дадим переменной х приращение
которая называется частичным приращением функции z=f(x;у) по переменной х. Аналогично величину
называют частичным приращением функции по переменной у. Если существует предел
то его называют частной производной функции z=f(x;у) в точке М (x;у) по переменной х и обозначают такими символами:
Аналогично
Из таких определений следует, что правила вычисления производных, совпадают с правилами дифференцирования функций одной переменной. Следует только помнить, что при вычислении частной производной по одной переменной остальные переменные считаются постоянными. Частные производные характеризуют скорость изменения функции в направлении соответствующих координатных осей. Частные производные от частных производных
Производные Частные производные от частных производных второго порядка называются частными производными третьего порядка и т. д.
|

 называется приделом функции f(x) если для любого
называется приделом функции f(x) если для любого 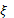 существует такое число
существует такое число 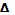 так что любое значение х из Х удовлетворяет любое и выполняется неравенство │f(x)-y₀│<
так что любое значение х из Х удовлетворяет любое и выполняется неравенство │f(x)-y₀│< 
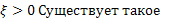 число Р зависящее от
число Р зависящее от 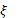 (>0). Что при всех значениях х
(>0). Что при всех значениях х  Х и удовлетворяет неравенству │х
Х и удовлетворяет неравенству │х  >Р
>Р (
( ,
, 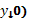 рассмотрим в ней предел p(M,
рассмотрим в ней предел p(M,  )=
)= 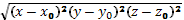 Число
Число 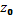 Называется пределом нескольких переменных.
Называется пределом нескольких переменных.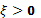 существует число
существует число  так, чтобы точка (х+
так, чтобы точка (х+ 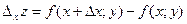 ,
,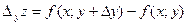

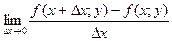 ,
, ,
,  ,
, 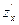 ,
, 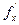 .
. =
= 
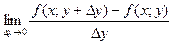 .
.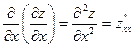 ,
, 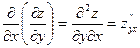 ,
, ,
, 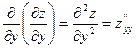 .
.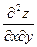 и
и  называются смешанными. Можно доказать, что если они непрерывны, то равны между собой.
называются смешанными. Можно доказать, что если они непрерывны, то равны между собой.


