Разветвление и слияние стрелок

Разветвление стрелки, изображаемое в виде расходящихся линий, означает, что все содержи­мое стрелки или его часть может появиться в каждом ответвлении стрелки. Разветвлением стрелок является присоединение к любой точке стрелки начала другой стрелки.

Слияние стрелок, изображаемое как сходящиеся вместе линии, указывает, что содер­жимое каждой ветви попадает в результирующую стрелку. Слиянием стрелок является присоединение к любой точке стрелки конца другой стрелки. Количество присоединяемых стрелок не ограничено.

Очередность присоединения стрелок друг к другу значима: от неё зависит порядок именования стрелок и наследование объектов стрелки.

Основной стрелкой называется та стрелка, к которой присоединяется стрелка-сегмент.

Правила механизма слияния/разветвления стрелок:

Если неименованная стрелка (для диаграммы IDEF0 неименованная стрелка обозначается надписью «#имя?») присоединяется к именованной стрелке, то она становится сегментом основной стрелки. При этом сегмент изображается на диаграмме без названия (для диаграммы IDEF0 надпись «#имя?» исчезает). Все Объекты, входящие в основную стрелку, теперь относятся и к сегменту.

Именованная стрелка сохраняет свое название и перечень Объектов при соединении её с другими стрелками.

Если неименованная стрелка становится именованной, то все неименованные сегменты, прикрепленные к ней, становятся сегментами основной стрелки: у них исчезает надпись «#имя?» (для диаграммы IDEF0) и они приобретают перечень Объектов основной стрелки.

В любой момент времени сегменту, не имеющему собственного названия, можно его присвоить. При этом сегмент становится именованной стрелкой со своим перечнем Объектов, если название сегмента отличается от названия основной стрелки.

Сегмент не может соединять две стрелки между собой или начинаться и кончаться на одной и той же стрелке.

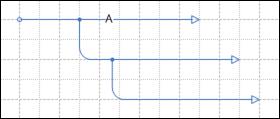
Ниже на рисунках приведено несколько типичных примеров разветвления стрелок. На Рис. 4.10.11 показана основная стрелка «А» с двумя сегментами, не имеющими собственных названий.

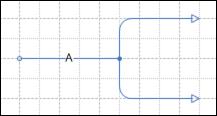
Рис. 4.10.11

Если первому сегменту присвоить другое название (например, «Б»), то второй сегмент по-прежнему будет показан без названия и приобретет перечень Объектов сегмента «Б». Изменение названий сегментов никак не влияет на основную стрелку «А».

На Рис. 4.10.12 показан другой вид разветвления: к концу стрелки «А» присоединены начала двух стрелок-сегментов. Если верхнему сегменту присвоить другое название, то основная стрелка «А» и нижний сегмент останутся без изменений.

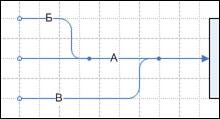
Рис. 4.10.12

Каждая стрелка в сложной разветвляющейся структуре может иметь собственное название и перечень Объектов (Рис. 4.10.13). Такие виды разветвления стрелок могут использоваться в различных комбинациях друг с другом.

Рис. 4.10.13

Правила действия механизма слияния стрелок аналогичны правилам механизма разветвления стрелок.

На диаграмме процесса в нотации IDEF0 при слиянии входящий конец стрелки-сегмента преобразуется в точку (Рис. 4.10.14).

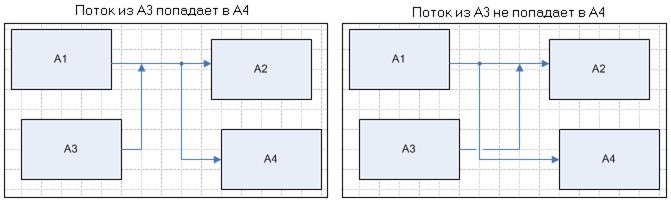
Рис. 4.10.14

На диаграммах процессов в нотациях Процесс и Процедура при слиянии стрелок конец стрелки отображается треугольником (Рис. 4.10.15).

Правило ручейка – ветвление стрелок осуществляется только по «течению» (Рис. 4.10.15).

Рис. 4.10.15