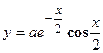
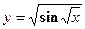
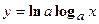

- Найти
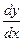

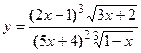
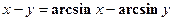
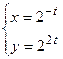
4. Показать, что функция 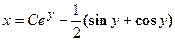 удовлетворяет уравнению
удовлетворяет уравнению 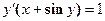
5. Найти 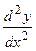
а)  в)
в) 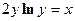
б) 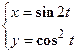
- В какой точке касательная к параболе
 образует с прямой
образует с прямой 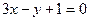 угол в 45°?
угол в 45°? - Построить дугу
 кривой
кривой  на отрезке
на отрезке  . Почему на дуге нет касательной, параллельной хорде АВ? Какое из условий теоремы Рояля здесь не выполнено?
. Почему на дуге нет касательной, параллельной хорде АВ? Какое из условий теоремы Рояля здесь не выполнено?
Вариант 25
- Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
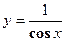
- Найти производную сложной функции


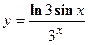


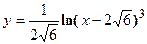

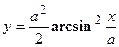
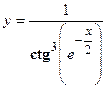
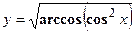

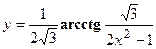

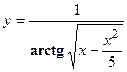
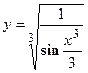
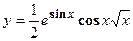
- Найти
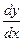
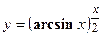


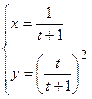
- Показать, что функция
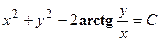 удовлетворяет уравнению
удовлетворяет уравнению 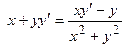
- Найти
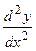
а)  в)
в) 
б) 
- При каком значении независимой переменной касательные к кривым
 и
и 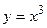 параллельны?
параллельны? - Показать, что производная
 функции
функции  имеет действительный корень в интервале (-1, 1).
имеет действительный корень в интервале (-1, 1).
Вариант 26
- Исходя из определения производной (не пользуясь формулами дифференцирования), найти производную функции

- Найти производную сложной функции
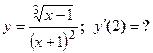
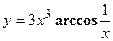
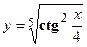
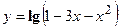
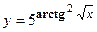
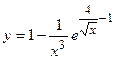
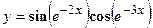


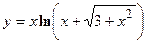

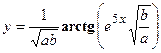

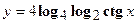
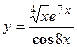
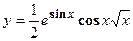
3. Найти 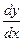

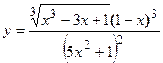

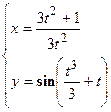
4. Показать, что функция 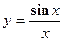 удовлетворяет уравнению
удовлетворяет уравнению 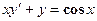 .
.
5. Найти 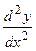
а)  в)
в) 
б) 
6. Составить уравнение касательной и нормали к кривой 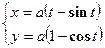 в точке, соответствующей значению параметра
в точке, соответствующей значению параметра 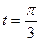 .
.
7. Построить график функции 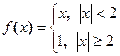 . Взяв на нем точки О(0; 0) и В(2; 1) показать, что между О и В на графике функции нет точки, касательная в которой была бы параллельна ОВ. Какие условия теоремы Лагранжа для этой функции на отрезке [0; 2] выполнены и какие нет?
. Взяв на нем точки О(0; 0) и В(2; 1) показать, что между О и В на графике функции нет точки, касательная в которой была бы параллельна ОВ. Какие условия теоремы Лагранжа для этой функции на отрезке [0; 2] выполнены и какие нет?
Вариант 27
1. Исходя из определения производной (не пользуясь формулами дифференцирования), найти производную функции 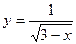 .
.
2. Найти производную сложной функции



 8
8
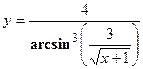

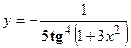

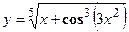

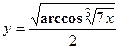
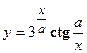
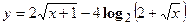
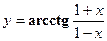


3. Найти 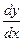
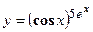

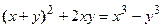

4. Показать, что функция 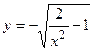 удовлетворяет уравнению
удовлетворяет уравнению 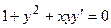 .
.
5. Найти 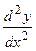
а)  в)
в) 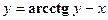
б) 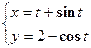
6. Написать уравнения касательных к гиперболе  в точках
в точках  и
и 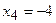 и найти угол между касательными.
и найти угол между касательными.
7. В какой точке касательная к кривой 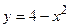 параллельна хорде, стягивающей точки А(-2; 0) и В(1; 3)? Пояснить графически.
параллельна хорде, стягивающей точки А(-2; 0) и В(1; 3)? Пояснить графически.
Вариант 28
1. Исходя из определения производной (не пользуясь формулами дифференцирования), найти производную функции  .
.
2. Найти производную сложной функции
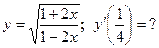
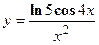
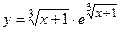

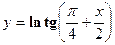

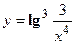


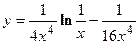
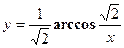

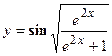



3. Найти 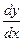

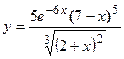


4. Показать, что функция  удовлетворяет уравнению
удовлетворяет уравнению 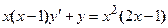 .
.
5. Найти 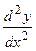
а)  в)
в) 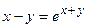
б) 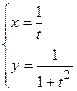
6. Составить уравнения касательной и нормали к кривой 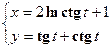 в точке, соответствующей значению параметра
в точке, соответствующей значению параметра  .
.
7. Показать, что на отрезке [-1; 2] теорема Лагранжа неприменима к функции  .
.
Вариант 29
- Исходя из определения производной (не пользуясь формулами дифференцирования), найти производную функции
 .
. - Найти производную сложной функции

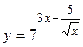
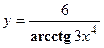

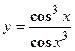


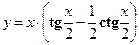
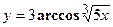

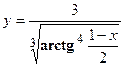

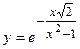

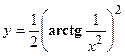
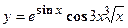
- Найти
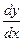
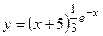
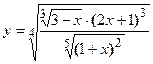

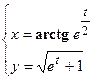
- Показать, что функция
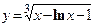 удовлетворяет уравнению
удовлетворяет уравнению  .
. - Найти
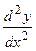
а) 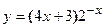 в)
в) 
б) 
- В какой точке параболы
 нужно провести касательную, чтобы она была перпендикулярна к биссектрисе первого координатного угла.
нужно провести касательную, чтобы она была перпендикулярна к биссектрисе первого координатного угла. - Проверить справедливость теоремы Ролля для функции
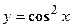 на отрезке
на отрезке  .
.
Вариант 30
- Исходя из определения производной (не пользуясь формулами дифференцирования), найти производную функции
 .
. - Найти производную сложной функции
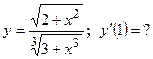
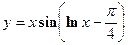



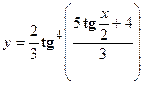


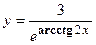
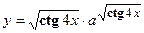
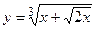
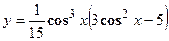




- Найти
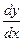

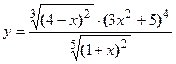
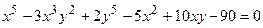
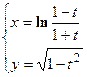 ё
ё
- Показать, что функция
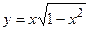 удовлетворяет уравнению
удовлетворяет уравнению  .
. - Найти
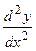
а)  в)
в) 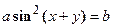
б) 
- Составить уравнения касательной и нормали к кривой
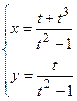 в точке, соответствующей значению параметра t = 2.
в точке, соответствующей значению параметра t = 2. - В какой точке касательная к кривой
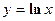 параллельна хорде стягивающей точки М1(1; 0) и М2(e; 1)?
параллельна хорде стягивающей точки М1(1; 0) и М2(e; 1)?

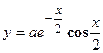
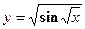
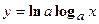

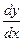

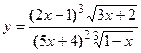
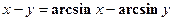
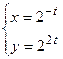
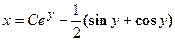 удовлетворяет уравнению
удовлетворяет уравнению 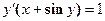
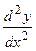
 в)
в) 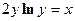
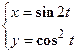
 образует с прямой
образует с прямой 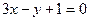 угол в 45°?
угол в 45°? кривой
кривой  на отрезке
на отрезке  . Почему на дуге нет касательной, параллельной хорде АВ? Какое из условий теоремы Рояля здесь не выполнено?
. Почему на дуге нет касательной, параллельной хорде АВ? Какое из условий теоремы Рояля здесь не выполнено?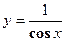


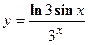


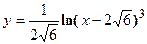

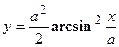
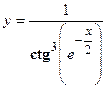
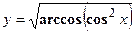

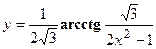

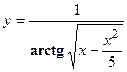
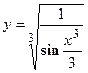
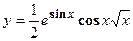
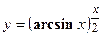


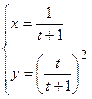
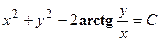 удовлетворяет уравнению
удовлетворяет уравнению 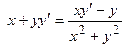
 в)
в) 

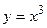 параллельны?
параллельны? функции
функции  имеет действительный корень в интервале (-1, 1).
имеет действительный корень в интервале (-1, 1).
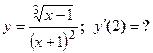
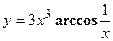
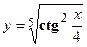
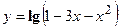
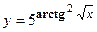
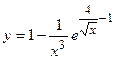
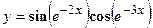


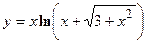

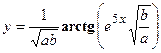

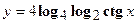
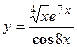

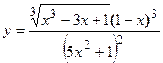

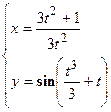
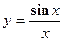 удовлетворяет уравнению
удовлетворяет уравнению 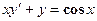 .
. в)
в) 

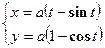 в точке, соответствующей значению параметра
в точке, соответствующей значению параметра 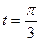 .
.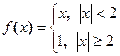 . Взяв на нем точки О(0; 0) и В(2; 1) показать, что между О и В на графике функции нет точки, касательная в которой была бы параллельна ОВ. Какие условия теоремы Лагранжа для этой функции на отрезке [0; 2] выполнены и какие нет?
. Взяв на нем точки О(0; 0) и В(2; 1) показать, что между О и В на графике функции нет точки, касательная в которой была бы параллельна ОВ. Какие условия теоремы Лагранжа для этой функции на отрезке [0; 2] выполнены и какие нет?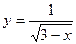 .
.


 8
8






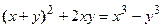

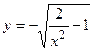 удовлетворяет уравнению
удовлетворяет уравнению 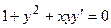 .
. в)
в) 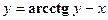
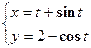
 в точках
в точках  и
и 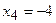 и найти угол между касательными.
и найти угол между касательными.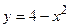 параллельна хорде, стягивающей точки А(-2; 0) и В(1; 3)? Пояснить графически.
параллельна хорде, стягивающей точки А(-2; 0) и В(1; 3)? Пояснить графически. .
.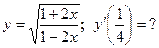




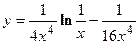
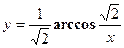

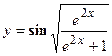



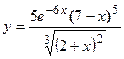


 удовлетворяет уравнению
удовлетворяет уравнению 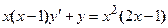 .
. в)
в) 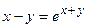
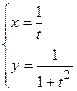
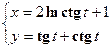 в точке, соответствующей значению параметра
в точке, соответствующей значению параметра  .
. .
. .
.







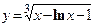 удовлетворяет уравнению
удовлетворяет уравнению  .
.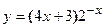 в)
в) 

 нужно провести касательную, чтобы она была перпендикулярна к биссектрисе первого координатного угла.
нужно провести касательную, чтобы она была перпендикулярна к биссектрисе первого координатного угла.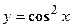 на отрезке
на отрезке  .
. .
.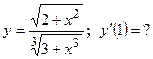










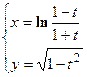 ё
ё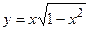 удовлетворяет уравнению
удовлетворяет уравнению  .
. в)
в) 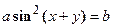

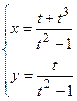 в точке, соответствующей значению параметра t = 2.
в точке, соответствующей значению параметра t = 2.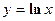 параллельна хорде стягивающей точки М1(1; 0) и М2(e; 1)?
параллельна хорде стягивающей точки М1(1; 0) и М2(e; 1)?


