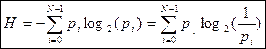Меры информации
меры информации. Существует три направления в определении мер. Это
Синтаксическая [1] мера информации оперирует с обезличенной информацией, не выражающей смыслового отношения к объекту. На синтаксическом уровне учитываются тип носителя и способ представления информации, скорость передачи и обработки, размеры кодов представления информации. На этом уровне информацию обычно называют данными, так как смысловая сторона при этом не имеет значения. Например, для плохо видящего человека существенным является размер и цвет шрифта. Если предполагается вводить данный текст в компьютер через сканер, важен формат бумаги Для анализа синтаксических мер вводится два понятия: объем информации (данных)- Vд(объемный подход) и количество информации в синтаксическом смысле – I (энтропийный подход). Определения количества информации и энтропии. Информация – это сведения об объектах и явлениях окружающей среды, их параметрах, свойствах и состоянии, которые уменьшают имеющуюся о них степень неопределённости и неполноты знаний и являются объектом хранения, преобразования, передачи и использования. Для измерения количества информации нужна единица измерения Подход к информации как мере уменьшения неопределенности знаний позволяет количественно измерять информацию, что чрезвычайно важно для информатики. Рассмотрим два классических примера. Пример1. Пусть у нас имеется монета, которую мы бросаем на ровную поверхность. С равной вероятностью произойдет одно из двух возможных событий — монета окажется в одном из двух положений: “орел” или “решка”. Перед броском существует неопределенность наших знаний (возможны два события), и, как упадет монета, предсказать невозможно. После броска наступает полная определенность, так как мы видим (получаем зрительное сообщение), что монета в данный момент находится в определенном положении. Это сообщение приводит к уменьшению неопределенности наших знаний в два раза. Пример2. игра "Угадай карту" Загадать карту, цель - "угадать" карту. Пусть имеется колода карт, содержащая 32 различные карты (все четыре шестерки отсутствуют). Начальная неопределенность знания составляет 32 возможных события. Чтобы определить карту, необходимо получить определенное количество информации. Можно отвечать только "да" и "нет". Необходимо выбрать следующую стратегию: последовательно, на каждом шаге уменьшать неопределенность знания в два раза. Для выбора дамы «пик» такими вопросами будут:
После пяти вопросов неопределенность устранена. Потребовалось количество информации, равное 5. Это количество характеризует число двоичных вопросов (ответы на которые имеют значения «да», «нет»). Т.е. для определения карты из колоды, состоящей из 32 карт, достаточно 5 бит информации, т.е. достаточно задать пять вопросов с ответами ДА или НЕТ, чтобы определить искомую карту. Пример3 Предположим, что у Вашего друга на одной из его восьми полок, стоящих друг на друге, лежит DVD-диск с новым фильмом. (на 5-ой Какое минимальное количество вопросов, беседуя со своим другом по телефону, надо задать, чтобы узнать, на которой из полок лежит DVD-диск? Если разделить область неизвестного пополам, то DVD может оказаться выше либо ниже границы. Вопрос можно построить так: "DVD выше четвёртой полки?" (или, что то же самое "DVD ниже пятой полки?"). Кратко друг должен отвечать только "да" или только "нет". Получив ответ "да", Вы исключаете из поиска полки 1-4. Затем снова делите пополам оставшуюся область и спрашиваете друга: "DVD на четной полке?" Получив ответ "нет", мы отбрасывает из области поиска полки 6 и 8. Последний вопрос может звучать так: "DVD на пятой полке?". Вы получите ответ либо "да", либо "нет". Так Вы узнаете, на которой из полок лежит фильм. После трех вопросов неопределенность устранена. Таким методом дихотомического деления (деления пополам) Вы каждый раз, получая однозначный ответ, уменьшаете область неизвестного (неопределённость наших знаний) в два раза. В 1946 г. американский ученый-статистик Джон Тьюки предложил название БИТ (BIT — аббревиатура от BInary digiT), одно из главных понятий XX века. Тьюки избрал бит для обозначения одного двоичного разряда, способного принимать значение 0 или 1. В 1948 г. Клод Э́лвуд Шеннон, американский инженер и математик, Впервые использовал слово bit как единицу измерения информации в статье A Mathematical Theory of Communication. "Математическая теория связи" За единицу количества информации приняли такое количество информации, при котором неопределенность уменьшается в 2 раза. Такая единица - «бит». бит (bit – bi nary digi t – двоичный разряд) – это количество информации, необходимое для различения двух равновероятных сообщений. Сообщение о том, что произошло одно событие из двух равновероятных, несёт 1 бит информации. Сообщение о том, что произошло одно событие из 32 равновероятных, несёт 5 бит информации. Сообщение о том, что произошло одно событие из восьми равновероятных, несёт 3 бита информации. Откуда взялись именно такие величины? В 1928 г. американский инженер Р. Хартли предложил научный подход к оценке сообщений. Если события равновероятны, то количество информации определяется по формуле Хартли I = log2 N Где N - количество равновероятных событий; I - количество бит в сообщении
Количество возможных событий N и количество информации I связаны между собой формулой: N = 2I Для наших примеров: 1) I = log2 2 2 = 2I 2 = 21 I =1 2) I = log2 32 32 = 2I 32 = 25 I =5 3) I = log2 8 8 = 2I 8 = 23 I =3 Данная формула позволяет определять: ü количество информации, если известно количество событий; ü количество возможных событий, если известно количество информации; Неопределенность неотъемлема от понятия вероятности. Вероятность - величина, которая может принимать значения в диапазоне от 0 до 1. Она может рассматриваться как мера возможности наступления какого-либо события, которое может иметь место в одних случаях и не иметь места в других.Если событие никогда не может произойти, его вероятность считается равной 0.Если событие происходит всегда, его вероятность равна 1.
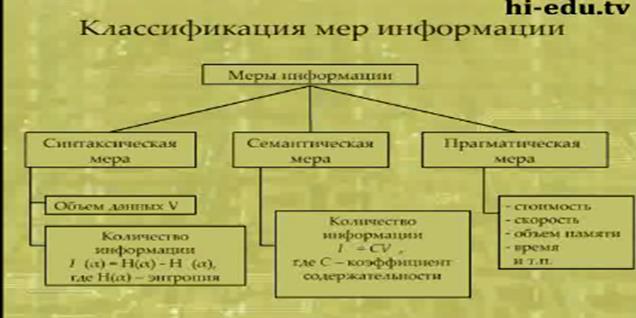
Уменьшение неопределенности всегда связано с выбором (отбором) одного или нескольких элементов (альтернатив) из некоторой их совокупности. Р. Хартли понимал, что сообщения имеют различную вероятность и, следовательно, неожиданность их появления для получателя неодинакова. Но, определяя количество информации, он пытался полностью исключить фактор «неожиданности». Поэтому формула Хартли позволяет определить количество информации в сообщении только для случая, когда появление символов равновероятно и они статистически независимы. На практике эти условия выполняются редко. При определении количества информации необходимо учитывать не только количество разнообразных сообщений, которые можно получить от источника, но и вероятность их получения. Клод Шеннон в 1948 г. предложил другую формулу определения количества информации, учитывающую возможную неодинаковую вероятность сообщений в наборе.
где I – количество информации; N – количество возможных событий; Pi – вероятность отдельных событий. суммарная вероятность полной группы событий равна 1. По свойству логарифма
Задача1: Какое количество информации будет содержать зрительное сообщение о цвете вынутого шарика, если в непрозрачном мешочке находится 50 белых, 25красных, 25 синих шариков 1) всего шаров 50+25+25=100 2) вероятности шаров 50/100=1/2, 25/100=1/4, 25/100=1/4 3)I= -(1/2 log21/2 + 1/4 log21/4 + 1/4 log21/4) = -(1/2(0-1) +1/4(0-2) +1/4(0-2)) = 1,5 бит Это выражение, повторяющее по форме выражение для энтропии в статистической механике, К. Шеннон по аналогии назвал энтропией и связал с понятием информации. Мерой количества информации Шеннон предложил считать функцию, названную им энтропией. Информацио́нная энтропи́я — мера неопределённости или непредсказуемости информации, неопределённость появления какого-либо символа первичного алфавита. энтропия - числовая характеристика, отражающая ту степень неопределенности, которая исчезает после проведения опыта, т. е. ПОСЛЕ ПОЛУЧЕНИЯ ИНФОРМАЦИИ, выраженная в битах. т.е. энтропия системы может рассматриваться как мера недостающей информации. Какова же связь энтропии с информацией? Количество информации мы будем обозначать символом I, энтропию – Н. Из определения энтропии следует, что Энтропия опыта равна той информации, которую мы получаем в результате его осуществления. H1 – начальная энтропия (до проведения опыта), H2 – энтропия после проведения опыта, то количество информации равно I=H1-H2 Количество информации, которое получено в ходе осуществления опыта это разность неопределенностей “до” и “после” опыта. Когда неопределенность снята полностью, количество полученной информации I равно изначально существовавшей неопределенности H. Такой подход принципиально изменил понятие информации. Под информацией теперь стали понимать не любые сообщения, передаваемые в системе связи, а лишь те, которые уменьшают неопределенность у получателя информации, и чем больше уменьшается эта неопределенность, т.е. чем больше снижается энтропия сообщения, тем выше информативность поступившего сообщения.
Итак, объем данных VД Объем данных VД в сообщении измеряется количеством символов (разрядов) в этом сообщении. В различных системах счисления один разряд имеет различный вес и соответственно меняется единица измерения данных: Ø в двоичной СС единица измерения- бит (bit – bi nary digi t – двоичный разряд). Ø в десятичной СС единица измерения – дит (десятичный разряд) Пример. Сообщение в двоичной СС в виде восьмиразрядного двоичного кода 11001011 имеет объем данных VД = 8 бит = 1 байт, сообщение в десятичной СС в виде числа 281934 имеет объем данных VД = 6 дит. Единицы измерения объема данных: 1 Килобайт = 1 Кб = 1024 байт = 210 байт 1 Мегабайт = 1 Мб = 1024 Кб = 210 Килобайт = 220 байт 1 Гигабайт = 1 Гб = 1024 Мб = 210 Мегабайт = 230 байт 1 Терабайт = 1 Тб = 1024 Гигабайт = 210 Гигабайт = 240 байт 1 Петабайт = 1 Тб = 1024 Терабайт = 210 Терабайт = 250 байт 1 Эксабайт = 1 Гб = 1024 Мб = 210 Мегабайт = 260 байт зеттабайт ZB 1021 зебибайт ZiB Збайт 270 йоттабайт YB 1024 йобибайт YiB Йбайт 280 Число 1024 как множитель при переходе к более высшей единице измерения информации имеет своим происхождением двоичную систему счисления (1024 — это десятая степень двойки 210).
|

 Нахождение логарифма b по основанию a - это нахождение степени, в которую нужно возвести a, чтобы получить b.
Нахождение логарифма b по основанию a - это нахождение степени, в которую нужно возвести a, чтобы получить b.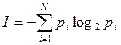 ,
,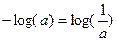 , поэтому эту формулу можно записать и во втором варианте, без минуса перед знаком суммы.
, поэтому эту формулу можно записать и во втором варианте, без минуса перед знаком суммы.