Аксиоматическое определение скалярного произведения на комплексном линейном пространстве. Следствия из аксиом. Унитарные пространства.
Уч.год. Вопросы, необходимые знать для получения оценки 4 или 5 (все вопросы без доказательств)
1. Понятие матрицы. Квадратные, треугольные, диагональные матрицы. Нулевая и единичная матрицы. Символ Кронекера. 2. Операции над матрицами: сложение, умножение на число, умножение матриц, транспонирование. Свойства этих операций. 3. Степени квадратной матрицы. 4. Понятие определителя. Основные свойства определителей. 5. Определение обратной матрицы. Формула для ее нахождения. 6. Критерий совместности системы линейных уравнений (теорема Кронекера–Капелли). 7. Однородные системы линейных уравнений. Количество решений. Фундаментальная система решений. 8. Определение линейного пространства и простейшие следствия из аксиом. 9. Определение линейной зависимости и независимости элементов линейного пространства. Свойства линейной зависимости и независимости. 10. Базис и координаты в линейном пространстве. Свойства координат векторов. 11. Матричный критерий линейной зависимости и независимости. 12. Определение матрицы перехода. 13. Определение линейного оператора и его простейшие свойства. Теорема о существовании линейного оператора. 14. Определение собственного вектора линейного оператора. 15. Характеристический многочлен и характеристические числа линейного оператора и его матрицы. Правило нахождения собственных векторов. 16. Определение приводимости квадратной матрицы к диагональному виду. Критерий приводимости квадратной матрицы к диагональному виду. 17. Присоединенные векторы и правило их нахождения. 18. Определение билинейной формы. 19. Квадратичные формы. 20. Канонический и нормальный виды квадратичной формы. 21. Определение знакоопределенной квадратичной формы. Необходимое условие знакоопределенности. 22. Критерий Сильвестра знакоопределенности квадратичных форм. 23. Аксиоматическое определение скалярного произведения на действительном линейном пространстве. Следствия из аксиом. Евклидовы пространства. 24. Ортогональные и ортонормированные системы векторов. 25. Выражение скалярного произведения через координаты перемножаемых векторов в ортонормированном базисе. 26. Определение самосопряженного оператора. Свойства собственных значений эрмитовых операторов и собственных векторов эрмитовых и симметричных операторов. 27. Определение изометрии. 28. Ортогональные операторы на евклидовой плоскости. 29. Ортогональные операторы в трехмерном евклидовом пространстве. 30. Симметричные операторы на евклидовой плоскости и в трехмерном евклидовом пространстве. 31. Общее определение тензора. Примеры тензоров. 32. Определение группы Вопросы, необходимые знать для получения оценки 6 или 7
1. Матрицы и линейные операции над ними. 2. Определение умножения матриц и свойства операции умножения. 3. Степени квадратной матрицы и их свойства. 4. Операция транспонирования матриц и ее свойства. 5. Понятие определителя. Теорема о разложении определителя по строке (столбцу). 6. Свойства определителей (с доказательством). 7. Теоремы аннулирования и замещения. 8. Определение обратной матрицы и ее свойства. Теорема существования и единственности (с доказательством). 9. Ранг матрицы и его свойства. Теорема об элементарных преобразованиях матрицы 10. Определение базисного минора матрицы. Теорема о базисном миноре. 11. Критерий совместности системы линейных уравнений (теорема Кронекера–Капелли)(с доказательством). 12. Однородные системы линейных уравнений. Количество решений, свойства решений. Фундаментальная система решений. 13. Определение линейного пространства и простейшие следствия из аксиом (с доказательством). 33. Определение линейной зависимости и независимости элементов линейного пространства. Свойства линейной зависимости и независимости(с доказательством). 34. Базис и координаты в линейном пространстве. Свойства координат векторов. 35. Матричный критерий линейной зависимости и независимости. 36. Определение размерности линейного пространства. Теорема о связи базиса и размерности. Следствия. 37. Определение подпространства линейного пространства и теорема о подпространствах. 38. Определение матрицы перехода и её свойства. 39. Определение матрицы перехода. Изменение координат вектора при изменении базиса.Линейное невырожденное преобразование переменных. 40. Определение линейного оператора и его простейшие свойства (с доказательством). 41. Определение матрицы линейного оператора.Связь координат вектора с координатами его образа. 42. Определение матрицы линейного оператора.Изменение матрицы линейного оператора при изменении базиса. Подобные матрицы. 43. Операции над линейными операторами. 44. Невырожденные линейные операторы. Теорема о матрице. 45. Обратный линейный оператор. 46. Определение изоморфизма линейных пространств. Теорема о размерности изоморфных пространств. 47. Определение и свойства собственных векторов (с доказательством). Характеристический многочлен и характеристические числа линейного оператора и его матрицы. Правило нахождения собственных векторов (с доказательством).. Лемма о решении вырожденной однородной системы линейных уравнений. 49. Определение приводимости квадратной матрицы к диагональному виду. Критерий приводимости квадратной матрицы к диагональному виду. 50. Присоединенные векторы и правило их нахождения. 51. Определение билинейной формы и различные способы её записи. 52. Изменение матрицы билинейной формы при изменении базиса. 53. Невырожденные и симметричные билинейные формы и их матрицы. 54. Квадратичные формы и их связь с билинейными формами. Различные способы записи квадратичной формы. Изменение матрицы квадратичной формы при изменении базиса. 55. Канонический и нормальный виды квадратичной формы. 56. Определение знакоопределенной квадратичной формы. Полуопределенные формы. Необходимое условие знакоопределенности (с доказательством). Исследование знакоопределенности по каноническому виду. 57. Критерий Сильвестра знакоопределенности квадратичных форм. 58. Аксиоматическое определение скалярного произведения на действительном линейном пространстве. Следствия из аксиом. Евклидовы пространства. Аксиоматическое определение скалярного произведения на комплексном линейном пространстве. Следствия из аксиом. Унитарные пространства. 60. Неравенства Коши – Буняковского и треугольника (с доказательством). 61. Ортогональные и ортонормированные системы векторов. Теорема о линейной независимости. 62. Процесс ортогонализации Грама-Шмидта. Пример. 63. Матрица Грама. Выражение скалярного произведения через координаты перемножаемых векторов. Изменение матрицы Грама при изменении базиса. 64. Ортогональные и унитарные матрицы и их свойства. Теорема о матрице перехода. Свойства эрмитовых и симметричных матриц. 65. Определение самосопряженного оператора. Теоремы о матрице, о собственных значениях и собственных векторах. Следствия из этих теорем. 66. Определение самосопряженного оператора и теорема об ортонормированном базисе. 67. Приведение квадратичной формы к каноническому виду с помощью ортогонального преобразования переменных. 68. Определение изометрии и теорема об её собственных значениях. 69. Определение изометрии и теорема о длинах. 70. Определение изометрии и теорема об ортонормированном базисе. 71. Матрицы ортогональных и унитарных операторов. 72. Ортогональные операторы на евклидовой плоскости. 73. Ортогональные операторы в трехмерном евклидовом пространстве. 74. Симметричные операторы на евклидовой плоскости и в трехмерном евклидовом пространстве. 75. Общее определение тензора. Примеры тензоров. 76. Общее определение тензора. Основные операции над тензорами. 77. Тензоры в евклидовом пространстве. Метрический тензор. Операции поднятия и опускания индексов. Тензоры в ортонормированных базисах. Евклидов (ортогональный) тензор. 78. Определение группы и простейшие следствия из аксиом. 79. Группа Лоренца.
Вопросы, необходимые знать для получения оценки 8,9 или 10
1. Матрицы и линейные операции над ними. 2. Определение умножения матриц и свойства операции умножения. 3. Степени квадратной матрицы и их свойства. 4. Операция транспонирования матриц и ее свойства. 5. Определение определителя. Леммы о разложении по первому столбцу, о равноправии строк и столбцов, о перестановке строк и столбцов (доказательство одной из трех). 6. Теорема о разложении определителя по строке (столбцу). Теорема Лапласа (без доказательства). 7. Свойства определителей. 8. Теоремы аннулирования и замещения. 9. Определение обратной матрицы и ее свойства. Теорема существования и единственности. 10. Матричные уравнения. Лемма о равносильности систем линейных уравнений и матричных уравнений. 11. Правило Крамера решения систем линейных уравнений. 12. Ранг матрицы и его свойства. Теорема об элементарных преобразованиях матрицы (без доказательства). 13. Определение базисного минора матрицы. Теорема о базисном миноре. 14. Теорема о линейной независимости строк и столбцов матрицы. Следствия. 15. Критерий совместности системы линейных уравнений (теорема Кронекера–Капелли). 16. Однородные системы линейных уравнений. Количество решений, свойства решений. Фундаментальная система решений. 17. Неоднородные системы линейных уравнений. Связь решений неоднородной системы и союзной к ней однородной. 18. Теорема о приведении матрицы к простейшему виду. Метод Гаусса решения систем линейных уравнений. 80. Определение линейного пространства и простейшие следствия из аксиом. 81. Определение линейной зависимости и независимости элементов линейного пространства. Свойства линейной зависимости и независимости. 82. Базис и координаты в линейном пространстве. Свойства координат векторов. 83. Матричный критерий линейной зависимости и независимости. 84. Определение размерности линейного пространства. Теорема о связи базиса и размерности. Следствия. 85. Определение размерности линейного пространства. Теорема о дополнении линейно независимой системы до базиса. 86. Определение аффинного пространства и следствия из аксиом. 87. 88. Определение подпространства линейного пространства и теорема о подпространствах. Теорема о размерности подпространства. 89. Линейные оболочки. Теорема о размерности линейной оболочки произвольной системы векторов. 90. Теорема о размерности линейной оболочки строк (столбцов) матрицы. 91. Определение суммы и пересечения подпространств линейного пространства. Теорема о сумме и пересечении подпространств. 92. Определение суммы и пересечения подпространств линейного пространства. Теорема о размерности прямой суммы. 93. Определение матрицы перехода и её свойства. 94. Определение матрицы перехода. Изменение координат вектора при изменении базиса. Линейное невырожденное преобразование переменных. 95. Понятие отображения. Произведение (композиция) отображений. Ассоциативность произведения. Тождественное отображение и его свойства. 96. Взаимно однозначное отображение. Обратное отображение. 97. Определение линейного оператора и его простейшие свойства. Теорема о существовании линейного оператора. 98. Определение матрицы линейного оператора. Связь координат вектора с координатами его образа. 99. Определение матрицы линейного оператора. Изменение матрицы линейного оператора при изменении базиса. Подобные матрицы. Лемма о подобных матрицах. 100. Операции над линейными операторами. Теорема о матрице. 101. Невырожденные линейные операторы. Теорема о матрице. 102. Невырожденные линейные операторы. Теорема о взаимной однозначности. 103. Обратный линейный оператор. Теорема о матрице. 104. Определение и свойства изоморфизма линейных пространств. 105. Определение изоморфизма линейных пространств. Теорема о размерности изоморфных пространств. 106. Определение изоморфизма линейных пространств. Теорема об изоморфности пространств одинаковой размерности. 107. Пространство линейных форм (сопряженное пространство). Взаимные базисы. 108. Определение и свойства собственных векторов. Собственные подпространства. Геометрическая кратность собственного значения. 109. Характеристический многочлен и характеристические числа линейного оператора и его матрицы. Правило нахождения собственных векторов. Лемма о решении вырожденной однородной системы линейных уравнений. 110. Лемма о диагональном виде матрицы линейного оператора. Определение приводимости квадратной матрицы к диагональному виду и первая теорема о приводимости. Следствие. Замечание о матрице, приводящей матрицу А к диагональному виду. 111. Лемма о связи геометрической и алгебраической кратностей собственного значения. 112. Определение приводимости квадратной матрицы к диагональному виду и вторая теорема о приводимости. 113. Присоединенные векторы и правило их нахождения. 114. Определение билинейной формы и различные способы её записи. 115. Изменение матрицы билинейной формы при изменении базиса. 116. Конгруэнтные матрицы. Лемма о конгруэнтных матрицах. Невырожденные билинейные формы. 117. Симметричные билинейные формы и их матрицы. 118. Квадратичные формы и их связь с билинейными формами. Различные способы записи квадратичной формы. Изменение матрицы квадратичной формы при изменении базиса. 119. Канонический и нормальный виды квадратичной формы. Метод Лагранжа (примеры). Закон инерции. 120. Определение знакоопределенной квадратичной формы. Полуопределенные формы. Необходимое условие знакоопределенности. Исследование знакоопределенности по каноническому виду. 121. Критерий Сильвестра знакоопределенности квадратичных форм. 122. Аксиоматическое определение скалярного произведения на действительном линейном пространстве. Следствия из аксиом. Евклидовы пространства. Псевдоевклидовы пространства. 123. Аксиоматическое определение скалярного произведения на комплексном линейном пространстве. Следствия из аксиом. Унитарные пространства. 124. Неравенства Коши – Буняковского и треугольника. 125. Ортогональные и ортонормированные системы векторов. Теорема о линейной независимости. 126. Процесс ортогонализации Грама-Шмидта. Пример. 127. Матрица Грама. Выражение скалярного произведения через координаты перемножаемых векторов. Изменение матрицы Грама при изменении базиса. 128. Подпространство евклидова (унитарного) пространства и его ортогональное дополнение. Разложение евклидова (унитарного) пространства в прямую сумму подпространств. Ортогональная проекция на подпространство. 129. Изоморфизм евклидовых пространств. 130. Ортогональные и унитарные матрицы и их свойства. Теорема о матрице перехода. Свойства эрмитовых и симметричных матриц. 131. Сопряженный линейный оператор. Теорема существования и единственности. Свойства сопряженных операторов. 132. Определение самосопряженного оператора. Теоремы о матрице, о собственных значениях и собственных векторах. Следствия из этих теорем. 133. Определение самосопряженного оператора. Теорема об инвариантности ортогонального дополнения. 134. Определение самосопряженного оператора и теорема об ортонормированном базисе. 135. Приведение квадратичной формы к каноническому виду с помощью ортогонального преобразования переменных. 136. Приведение уравнений поверхностей второго порядка к каноническому виду (решение задач). 137. Определение изометрии и теорема об её собственных значениях. 138. Определение изометрии и теорема о длинах. 139. Определение изометрии и теорема об ортонормированном базисе. 140. Определение изометрии и теорема об обратном операторе. Матрицы ортогональных и унитарных операторов. Теорема об инвариантности ортогонального дополнения (без доказательства). 141. Ортогональные операторы на евклидовой плоскости. 142. Ортогональные операторы в трехмерном евклидовом пространстве. 143. Симметричные операторы на евклидовой плоскости и в трехмерном евклидовом пространстве. 144. Общее определение тензора. Примеры тензоров. 145. Общее определение тензора. Алгебраические операции над тензорами. Прямой тензорный признак. 146. Общее определение тензора. Обратный тензорный признак(без доказательства). 147. Преобразования взаимных базисов. 148. Тензоры в евклидовом пространстве. Метрический тензор. Контравариантные и ковариантные компоненты вектора. 149. Операции поднятия и опускания индексов. Тензоры в ортонормированных базисах. Евклидов (ортогональный) тензор. 150. Определение группы и простейшие следствия из аксиом. 151. Группа Лоренца.
|

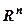 как пример аффинного, евклидова и метрического пространств.
как пример аффинного, евклидова и метрического пространств.


