Свойства оценок МНК
Прежде были рассмотрены способы формальных проверок статистической достоверности коэффициентов регрессии и корреляции с помощью t-критерия Стьюдента, F-критерия Фишера и Z-преобразования (для коэффициентов корреляции). При использовании этих критериев делаются предположения относительно поведения остатков ei=yi-ŷi на формальных проверках статистической достоверности коэффициентов регрессии и корреляции с помощью t-критерия Стьюдента, F-критерия Фишера и Z-преобразования (для коэффициентов корреляции). При использовании этих критериев делаются предположения относительно поведения остатков ei — остатки представляют собой независимые случайные величины и их среднее значение равно 0; они имеют одинаковую (постоянную) дисперсию и подчиняются нормальному распределению. Статистические проверки параметров регрессии, показателей корреляции основаны на непроверяемых предпосылках распределения случайной составляющей ei. Они носят лишь предварительный характер. После построения уравнения регрессии проводится проверка наличия у оценок ei, (случайных остатков) тех свойств, которые предполагались. Связано это с тем, что оценки параметров регрессии должны отвечать определенным критериям. Они должны быть несмещенными, состоятельными и эффективными. Эти свойства оценок, полученных по МНК, имеют чрезвычайно важное практическое значение в использовании результатов регрессии и корреляции. Коэффициенты регрессии, найденные исходя из системы нормальных уравнений, представляют собой выборочные оценки характеристики силы связи. Их несмещенность является желательным свойством, так как только в этом случае они могут иметь практическую значимость. Несмещенность оценки означает, что математическое ожидание остатков равно нулю. Следовательно, при большом числе выборочных оцениваний остатки не будут накапливаться и найденный параметр регрессии b, можно рассматривать как среднее значение из возможного большого количества несмещенных оценок. Если оценки обладают свойством несмещенности, то их можно сравнивать по разным исследованиям. Для практических целей важна не только несмещенность, но и эффективность оценок. Оценки считаются эффективными, если они характеризуются наименьшей дисперсией. Поэтому несмещенность оценки должна дополняться минимальной дисперсией. В практических исследованиях это означает возможность перехода от точечного оценивания к интервальному. Степень реалистичности доверительных интервалов параметров регрессии обеспечивается, если оценки будут не только несмещенными и эффективными, но и состоятельными. Состоятельность оценок характеризует увеличение их точности с увеличением объема выборки. Большой практический интерес представляют те результаты регрессии, для которых доверительный интервал ожидаемого значения параметра регрессии b, имеет предел значений вероятности, равный единице. Иными словами, вероятность получения оценки на заданном расстоянии от истинного значения параметра близка к единице. Указанные критерии оценок (несмещенность, состоятельность, эффективность) обязательно учитываются при разных способах оценивания. Метод наименьших квадратов строит оценки регрессии на основе минимизации суммы квадратов остатков. Поэтому очень важно исследовать поведение остаточных величин регрессии ei. Условия, необходимые для получения несмещенных, состоятельных и эффективных оценок, представляют собой предпосылки МНК, соблюдение которых желательно для получения достоверных результатов регрессии. Для того, чтобы полученные МНК оценки a и b обладали желательными свойствами, сделаем следующие предпосылки об отклонениях ei: 1) величина ei является случайной переменной; 2) математическое ожидание ei, равно нулю: М[ e i] = 0; 3) дисперсия ei постоянна: D[ ei ] = D[ ei ] = s 2 для всех i,j; 4) значения ei независимы между собой. Откуда вытекает, в частности, что
Известно, что, если условия 1)-4) выполняются, то оценки, сделанные с помощью МНК, обладают следующими свойствами: 1) Оценки являются несмещенными, т.е. математическое ожидание оценки каждого параметра равно его истинному значению: М[а] = a, М[b] = b. Это вытекает из того, что М[ei] = 0, и говорит об отсутствии систематической ошибки в определении положения линии регрессии. 2) Оценки состоятельны, то есть дисперсия оценок параметров при возрастании числа наблюдений стремится к нулю: Иначе говоря, если n достаточно велико, то практически наверняка a близко к a, а b близко к b: надежность оценки при увеличении выборки растет. 3) Оценки эффективны, они имеют наименьшую дисперсию относительно истинного значения оцениваемых параметров a и b по сравнению с любыми другими оценками, линейными относительно величин уi. В англоязычной литературе такие оценки называются BLUE (Best Linear Unbiased Estimators - наилучшие линейные несмещенные оценки). Перечисленные свойства не зависят от конкретного вида распределения величин ei, тем не менее, обычно предполагается, что они распределены нормально N(0,s2). Эта предпосылка необходима для проверки статистической значимости сделанных оценок и определения для них доверительных интервалов. При ее выполнении оценки МНК имеют наименьшую дисперсию не только среди линейных, но среди всех несмещенных оценок. Если предположения 3) и 4) нарушены, то есть дисперсия возмущений непостоянна и/или значения ei связаны друг с другом, то свойства несмещенности и состоятельности сохраняются, но свойство эффективности - нет. В тех случаях, когда все предпосылки выполняются, оценки, полученные по МНК будут наилучшими (состоятельными, несмещенными, эффективными), а также будут совпадать с оценками, полученными по методу максимального правдоподобия. Иначе оценки, полученные по МНК, не будут наилучшими. Поэтому модель нужно корректировать.
Рассмотрим предпосылки относительно случайных возмущений (остатков): 1) Случайный характер возмущений (остатков). Строится график зависимости остатков ei=yi-ŷi от теоретических значений результативного признака. Если на графике получена горизонтальная полоса, то остатки ei представляют собой случайные величины и МНК оправдан, теоретические значения ŷ хорошо аппроксимируют фактические значения y.
· · · · · · · ·
· · · · · · · · · · ·
Если ei зависит от ŷ, то возможны следующие случаи: - остатки не случайны (а); - остатки носят систематический характер, в данном случае отрицательные значения e соответствуют низким значениям ŷ, а положительные – высоким значениям (б); - остатки не имеют постоянной дисперсии (в).
· · · · · · · · а б в
2) Нулевая средняя величина остатков, не зависящая от Хi. Это означает, что å(y-ŷ)=0. Это выполнимо для линейных моделей и моделей, нелинейных относительно включаемых переменных. Для моделей, нелинейных по оцениваемым параметрам и приводимых к линейному виду логарифмированием, средняя величина остатков равна нулю для логарифмов исходных данных. так, для моделей вида: Y=a*X1b1*X2b2*...*Xkbk*e, å(lny-(lny)¢)=0. 3) Гомоскедастичность – дисперсия каждого отклонения ei одинакова для всех значений Хi. Данная предпосылка необходима для получения состоятельных оценок. Если условие равенства для каждого значения фактора Хi дисперсий остатков ei, не соблюдается, то имеет место гетероскедастичность. Наличие гетероскедастичности можно наглядно видеть из поля корреляции.
4) Отсутствие автокорреляции остатков. Значения ei распределены независимо друг от друга. Данная предпосылка необходима для получения состоятельных оценок. 5) Остатки подчиняются нормальному распределению. Данная предпосылка позволяет проводить проверку параметров регрессии и корреляции с помощью критериев t, F. Вместе с тем, оценки регрессии, найденные с применением МНК, обладают хорошими свойствами даже при отсутствии нормального распределения остатков, т.е. при нарушении данной предпосылки. Предпосылки относительно регрессоров (Х): 3) Регрессоры – случайные переменные, т.е. они не зависят от случайных остатков. Строится график зависимости случайных остатков от регрессоров. Если остатки на графике расположены в виде горизонтальной полосы, то они независимы от значений Х. Если же график показывает наличие зависимости ei и Хi, то модель неадекватна. Причины неадекватности могут быть разные. Возможно, нарушена третья предпосылка МНК и дисперсия остатков не постоянна для каждого значения фактора Хi. Может быть, неправильна спецификация модели и в нее необходимо ввести дополнительные члены от Хi, например, Хi2, или преобразовать значения y. Скопление точек в определенных участках значений фактора Хi говорит о наличии систематической погрешности модели. Корреляция случайных остатков с факторными признаками позволяет проводить корректировку модели, в частности использовать кусочно-линейные модели.
|

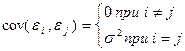
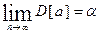 ;
; 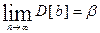

 e · · · · · · · ·
e · · · · · · · · ŷ
ŷ · · · · · · · · ·
· · · · · · · · ·


 e e e
e e e

 · · · · · · · · · · · ·
· · · · · · · · · · · · · · · · · · · · · · · · · · · ŷ
· · · · · · · · · · · · · · · ŷ · · · · · · · · · · · · ·
· · · · · · · · · · · · ·


