Вычислимость по Тьюрингу.
С помощью машины Тьюринга формализуется интуитивное понятие вычислимости (а тем самым и интуитивное понятие алгоритма). Пусть даны два алфавита А и В, такие, что А∩B≠{Ø}. Рассмотрим подмножество LÍ(A*)n, т.е. совокупности из n слов в алфавите А (A*)n = {(w1, w2, …, wn | wi Î A*}, где А* - множество слов над алфавитом А. n-местной частичной функцией из (А*)n (совокупности n слов над алфавитом А) в В* называется правило: f(w1, w2, …, wn) = w Î В* т.е. совокупности n слов (w1, w2, …, wn) Î (A*)n ставится в соответствие слово w Î В*, где А∩B≠{Ø}. Область определения функции f: Def(f) = LÍ(A*)n, т.е. совокупности n слов над алфавитом А. Область значений функции f: Im(f) = {wÎ B*| если существует совокупность из n слов (w1, w2, …, wn) Î (A*)n, w = f(w1, w2, …, wn) }. Под вычислимой функцией понимается функция, которая может быть вычислена с помощью некоторого алгоритма. Пусть МТ Т имеет рабочий алфавит А U В. будем говорить, что МТ Т определяет n-местную частичную функцию fT, отображающую (A*)n в В*, если выполняются следующие условия: 1. Совокупность n слов (w1, w2, …, wn) Î Def(fТ) тогда и только тогда, когда имеет место отношение <bw1bw2b…bwn(b)b>Þ*<bjbw(b)yb> (т.е. МТ Т начав работу в начальной ситуации S0 за конечное число шагов остановится в ситуации S) S0 Þ* S, где слово j, y Î (А È В È {b})* - расширение рабочего алфавита МТ Т. w Î B*, при этом слово w является значением функции fТ, т.е. w = fT(w1, w2, …, wn) 2. Совокупность n слов (w1, w2, …, wn)ÏDef(fT), если: МТ неприменима к начальным данным, либо w Ï B*, либо в рабочей ячейке в результате останова МТ содержится не буква b, либо рабочая ячейка не следует за словом w. Частичная функция f:(A*)n®B* (задающая отображение) называется вычислимой по Тьюрингу (ВТ-функцией), если существует Мт Т с рабочим алфавитом А È В, такая что n-местная частичная функция fТ:(A*)n®B*, определяемая этой МТ, совпадает с f (т.е. fT=f). О любой такой МТ говорят, что она вычисляет функцию f. Если МТ Т' моделирует МТ Т, то эти машины вычисляют одну и туже функцию f. Практическая вычислимость - это вычислимость, которая реализуется с помощью физического автомата и является значительно более узким понятием, чем вычислимость по Тьюрингу. Функция f:(A*)n®B* называется нормированно вычислимой по Тьюрингу (НВТ-функцией), если существует МТ Т, которая вычисляет f и при этом удовлетворяет следующим требованиям: 1. Если совокупность из n слов (w1, w2, …, wn)ÏDef(f),, то МТ начав работу с ситуации <bw1bw2b…bwn(b)b> никогда не остановится. 2. Если (w1, w2, …, wn) Î Def(f), то справедливо отношение <bw1bw2b…bwn(b)b>Þ*<bw1bw2b…bwn(b)wb>, где w=fT(w1…wn) Смысл нормированного вычисления состоит в том, что при таком вычислении часть ленты, расположенная левее символа b, непосредственно предшествующего слову w1, не меняется и не влияет на работу МТ Т. при нормированном вычислении головка не должна заходить левее указанного символа b. Теорема. Всякая вычислима по Тьюрингу функция (ВТ-функуция) является НВТ-функцией. Пример 1 (вычислимой функции). Моделирование работы Машины Поста. Функция f(x, y) = x + y, определённая на множестве пар неотрицательных целых чисел, является "вычислимой в интуитивном смысле"; покажем что она вычислима и в смысле Тьюринга. Для этого построим МТ М с алфавитом {b, ½} такую, что x + y = fT(x, y). Подобная машина должна, имея на ленте коды Легко убедиться, что следующая машина выполняет поставленную задачу: q1|βq2 стирается первая палочка первого кода q2βЛq3 q3|βq4 стирается вторая палочка первого кода q3ββq3
q5|Лq5 головка не дойдёт до несобственного символа q5β|q6 заменяем несобственный символ палочкой q4|βq4 останов Здесь машина останавливается, поскольку ситуации q4β нет ни в одной команде. В этот момент на ленте ровно x + y палочек. Пример 2 (пример частично вычислимой функции). Функция g(x, y) = x - y определена лишь для тех пар, у которых x ≥ y, покажем, что она частично вычислима по Тьюрингу. Для этого мы построим машину Тьюринга М, выполняющую вычитание. Пусть на ленте имеются коды q1|βq1 стирается самая левая палочка в q1βЛq2 лента сдвигается на одну ячейку влево, q2|Лq2 лента сдвигается влево, пока головка не дойдёт до конца кода q1βЛq3 головка переходит через пробел, разделяющий q3|Лq3 лента сдвигается влево, пока головка не дойдёт до конца кода q3βПq4 шаг назад на первый символ q4|βq4 стираем обозреваемый символ, q4βПq5 делаем шаг вправо, q5|Пq6 проверяем, если обозреваем палочку, то продолжаем вычисления, иначе машина останавливается, так как отсутствует команда q5β, q6|Пq6 сдвигаемся вправо, пока не встретим начало кода q6βПq7 переходим через пробел, разделяющий q7|Пq8 если в q7βПq7 если в q8|Пq8 лента сдвигается до начала кода q8βЛq1 головка устанавливается так, что обозревается самая левая палочка "остатка" кода Пример 3 (нормированные вычисления). Построить МТ М, делающую нормированные вычисления <bw(b)b>Þ*<bwbw1(b)b>, где w, w1 Для этого необходимо вначале скопировать исходные данные, а затем осуществлять прибавление 1, т.е. вначале необходимо построить копировальную машину <bw(b)b>Þ*<bwbw(b)b>, а затем строить МТ <bw bw(b)b>Þ*<bwbw1(b)b>, делающую нормированные вычисления и прибавляющую 1 к любому второму числу за конечное число тактов.
|

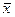 и
и 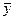 (
( ½,
½, 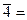 ½½½½½), разделённые пустой ячейкой, получать из этой записи x + y палочек (не обязательно подряд). Заметим, что x + y = <
½½½½½), разделённые пустой ячейкой, получать из этой записи x + y палочек (не обязательно подряд). Заметим, что x + y = < 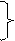 q4βЛq5 лента сдвигается до тех пор, пока
q4βЛq5 лента сдвигается до тех пор, пока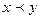 ), машина будет работать вечно, сдвигая ленту вправо,
), машина будет работать вечно, сдвигая ленту вправо,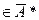 , A={1, 0}, w1=w+1, т.е. должны быть сохранены исходные данные.
, A={1, 0}, w1=w+1, т.е. должны быть сохранены исходные данные.


