Машина Тьюринга
Одним из способов формализации понятий вычислимости и алгоритма состоит в рассмотрении некоторой идеализированной вычислительной машины, которой должны быть присуще простота и архитектурное строение не должно резко отличаться от реальной вычислительной машины. Концепция абстрактной вычислительной машины была предложена Аланом Тьюрингом в 1936 году. Он показал возможность существования универсальной вычислительной машины (машины Тьюринга), способной выполнить любую эффективную процедуру. Машина Тьюринга - это гипотетическая вычислительная машина (автомат), использовавшаяся в качестве математической абстракции А.Тьюрингом с целью уточнения эффективного процесса (алгоритма) вычислений. С точки зрения формального описания машина Тьюринга есть совокупность следующих пяти компонент: 1. Управляющего устройства, способного принимать некоторое число состояний, которые соответствуют различным комбинациям состояний внутренних элементов электронной машины (ячейки памяти, электронные схемы и т.п.); 2. Ленты, разделённой на бесконечное число ячеек (≥1). На ленте выбрано направление, называемое направлением слева на право. Соответственно этому на ленте выделяются крайняя слева и крайняя справа ячейки; каждая ячейка, кроме крайней слева, имеет единственную соседнюю слева, каждая ячейка, кроме крайней справа, имеет единственную соседнюю справа; 3. Головки, которая в каждый момент работы машины находится в некоторой ячейке ленты и считывает информацию из этой ячейки. Головка может работать в каждый момент только с одной ячейкой ленты. При этом она может заменять прочитанный символ другим символом; 4. Двух конечных алфавитов - внешнего
и внутреннего
называемого также множеством состояний. Внутренний алфавит - это конечный алфавит символов, которые подаются на вход машины Тьюринга и выдаются на выходе. Внутренний алфавит - это конечный алфавит символов, комбинации которых определяют внутреннее состояние машины Тьюринга. а -1 - пограничный маркер, стоящий справа, q0 - начальное состояние машины Тьюринга. Командой называется выражение одного из следующих типов: qiajakqm qiajПqm qiajЛqm 5. Программы машины - конечного множества слов специального вида, называемых командами. Правильным вычислением машины Тьюринга М мы будем называть последовательность (s0, s1, …, sp) конфигураций этой машины такую, что: Для каждого i-0, … p-1 ситуация si+1 получается из si выполнением команды машины М; s0 - начальная конфигурация; sр - заключительная конфигурация; Ситуацией называется состояние машины вместе с указанием, какая ячейка обозревается и всего того, что напечатано на ленте. Формализацией машины Тьюринга называется набор Работа машины Тьюринга. Машина Тьюринга работает следующим образом: в каждой ситуации, определённой внутренним состоянием управляющего устройства и символом, прочитанным на ленте, машина срабатывает, переходя в другое состояние и продвигая ленту определённым образом. Ячейку, обозреваемую головкой в данный момент, называют рабочей ячейкой. Выполнение каждой команды МТ состоит в следующем: · Изменить содержимое рабочей ячейки aj на ak, т.е. в рабочую ячейку записывается какая-нибудь буква из · Головка передвигается на одну ячейку влево или вправо либо остаётся на месте; · Головка переводится в новое состояние, которое может и совпадать и со старым. Если команда не меняет буквы, записанной в рабочей ячейке, не сдвигает головки и не меняет её состояние, то такую команду будем называть командой останова. Перед началом работы МТ на её ленту записываются начальные данные: одно или несколько слов над алфавитом Слова отделяются друг от друга несобственной буквой В начале работы МТ головка приводится в начальное состояние q0 и помещается над начальной рабочей ячейкой, которая определённым и фиксированным для каждой конкретной МТ образом расположена относительно начальных данных. Начав работу МТ может, в зависимости от начальных данных: · Через конечное число тактов (шагов) приступить к выполнению команды
которая ничего не изменяет, и остановится. При этом на ленте оказывается записанной новая последовательность слов, которая представляет собой результат работы МТ. · МТ никогда не останавливается либо возникает пара (q, a), для которой не определена команда МТ. В этом случае считается, что МТ неприменима к соответствующим начальным данным. На множество команд, задающих машину Тьюринга, наложено требование, чтобы начальные пары символов всех команд были различны. Машину, для которой это требование выполнено, мы назовём детерминированной. Конфигурацией называется выражение, удовлетворяющее следующим условиям: · Оно не содержит вхождений символов П и Л; · Оно содержит ровно одно вхождение символа типа qi; · Это вхождение символа qi не занимает в выражении крайней правой позиции.
|



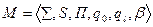 , где
, где  - внешний алфавит, S - внутренний алфавит, П - программа машины, q0 - начальное состояние, ql - заключительное состояние,
- внешний алфавит, S - внутренний алфавит, П - программа машины, q0 - начальное состояние, ql - заключительное состояние,  - несобственный символ алфавита, пробел (бланк).
- несобственный символ алфавита, пробел (бланк).