Ответ: Если какой-либо вектор можно представить в виде линейной комбинации, то говорят о линейной зависимости данного вектора от элементов комбинации.
Точнее, говорят так: некоторая совокупность элементов векторного пространства называется линейно зависимой, если существует равная нулю линейная комбинация элементов данной совокупности или
где не все числа Линейная зависимость векторов означает, что какой-то вектор заданной совокупности линейно выражается через остальные векторы. Каждая матрица представляет собой совокупность векторов (одного и того же пространства). Две такие матрицы — две совокупности. Если каждый вектор одной совокупности линейно выражается через векторы другой совокупности, то на языке теории матриц этот факт описывается при помощи произведения матриц: § если строки матрицы C линейно зависят от строк матрицы B, то C = AB для некоторой матрицы A; § если столбцы матрицы C линейно зависят от столбцов другой матрицы A, то C = AB для некоторой матрицы B.
16.Теорема о ранге матриц. Ответ:Ранг матрицы А равен максимальному числу линейно независимых столбцов (или равен рангу системы столбцов матрицы А) 17. Необходимом и достаточном условии равенства нулю определителя. Ответ:Определитель матрицы равен нулю 18.Система линейных алгебраических уравнений, матричная запись, формулы Крамера. Ответ: Система m линейных уравнений с n неизвестными (или, линейная система) в линейной алгебре — это система уравнений вида
Система линейных уравнений может быть представлена в матричной форме как:
1)x i = D i / D. 2) D = det (ai j) 3) D × x i = D i (i = 19.Теорема Кронекера-Капелли. Ответ: Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных. 20.Методы решения неоднородной системы линейных алгебраических уравнений. Ответ: 1. Решение матричного уравнения(Запишем систему в матричном виде и решим матричное уравнение). 2. Вычисление решения системы линейных уравнений по формулам Крамера. 3. Решение системы линейных уравнений методом Гаусса. 21.Необходимое и достаточное условие существования нулевого решения однородной системы линейных алгебраических уравнений. Ответ: Если система имеет единственное решение то это решения называется нулевым. Если система имеет несколько решений то среднее арифметическое этих решений является нулевым. 22.Методы решения однородных систем уравнения. Ответ: путем нахождения фср. 23.Теорема о фундаментальной системе решений. 24.Связь решений однородных и неоднородных систем линейных алгебраических уравнений. 25.Линейное пространство,размерность,базис.
|

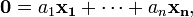
 равны нулю; если такой нетривиальной комбинации не существует, то данная совокупность векторов называется линейно независимой.
равны нулю; если такой нетривиальной комбинации не существует, то данная совокупность векторов называется линейно независимой.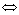 матрица содержит строку, являющуюся линейной комбинацией остальных строк матрицы.
матрица содержит строку, являющуюся линейной комбинацией остальных строк матрицы.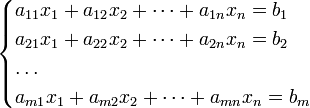

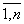 ).
).


