Ответ: Метод Гаусса—Жордана
Обратная матрица - это матрица, при умножении на которую исходная матрица дает в результате единичную матрицу E. Обратную матрицу можно найти только у квадратной матрицы, т.е. у матрицы, у которой число строк равняется числу столбцов. Теорема условия существования обратной матрицы Для того чтобы матрица имела обратную матрицу необходимо и достаточно, чтобы она была невырожденной. Матрица А = (А1, А2,...Аn) называется невырожденной, если векторы-столбцы являются линейно независимыми. Число линейно независимых векторов-столбцов матрицы называется рангом матрицы
10. Нахождение и свойства обратной матрицы. Ответ: Метод Гаусса—Жордана Возьмём две матрицы: саму A и единичную E. Приведём матрицу A к единичной матрице методом Гаусса—Жордана. После применения каждой операции к первой матрице применим ту же операцию ко второй. Когда приведение первой матрицы к единичному виду будет завершено, вторая матрица окажется равной A−1. При использовании метода Гаусса первая матрица будет умножаться слева на одну из элементарных матриц Λ i (трансвекцию или диагональную матрицу с единицами на главной диагонали, кроме одной позиции):
Вторая матрица после применения всех операций станет равна Λ, то есть будет искомой. Сложность алгоритма — O (n 3).
|
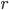. Поэтому можно сказать, что для того, чтобы существовала обратная матрица, необходимо и достаточно, чтобы ранг матрицы равнялся ее размерности, т.е. r = n.
.
.
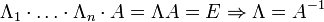