умов кристалізації, вони мають неправильну форму і називаються іноді кристалітами, а іноді зернами.
Періодична система елементів
умов кристалізації, вони мають неправильну форму і називаються іноді кристалітами, а іноді зернами. Чисті метали в звичайному структурному стані мають низьку міцність і не забезпечують у багатьох випадках необхідних властивостей. Тому їх застосовують порівняно рідко. Необхідно зазначити, що поняття чистий метал є дуже умовним. Будь-який чистий метал у більшій або в меншій кількості містить домішки і, отже, повинен розглядатися як сплав. Надалі під терміном чистий метал будемо розуміти метал, що містить 99,99 - 99,999 % основного металу. В усіх інших випадках мається на увазі технічно чистий метал з малою кількістю домішок (99,5-99,4), який одержується звичайними промисловими способами.
Найбільш широко використовують сплави. Сплави одержують сплавленням або спіканням (рідко - осадженням) двох або більше металів або металів з неметалами. Вони мають характерні для металевого стану властивості. Хімічні елементи, що утворюють сплав, називають компонентами. Сплав може складатися з двох або більшої кількості компонентів. Для розгляду будови, перетворень і властивостей металів і сплавів введемо поняття “система”, “фаза” і “структура”, які широко використовуються в металознавстві Системою називають сукупність фаз, що знаходяться в стані рівноваги. Фазою називають однорідну складову частину системи, що має певний склад, кристалічну будову, властивості і той же агрегатний стан і яка відділена від інших частин системи поверхнями розділу. Так, однорідний чистий метал або сплав є однофазною системою. Стан, коли одночасно присутні рідкий сплав (метал) і кристали, буде являти собою двофазну систему. Якщо у твердому сплаві будуть, наприклад, зерна металевої матриці і карбідні частки, то цей сплав також буде двофазним. Під структурою розуміють форму, розміри й характер взаємного розташування відповідних фаз у металах або сплавах. Структурними складовими сплаву називають відособлені частини сплаву, що мають однакову будову з властивими їм характерними рисами. Розрізняють макроструктуру (будову металу або сплаву, яку видно неозброєним оком або при незначному збільшенні (у 30 - 40 разів) та мікроструктуру (будову металу або сплаву, що спостерігається за допомогою мікроскопу при великих збільшеннях).
1.2. Атомно-кристалічна структура металів Під атомно-кристалічною структурою розуміють взаємне розташування атомів, існуюче в кристалі. Кристал складається з атомів (іонів), розташованих у певному порядку, який періодично повторюється у трьох вимірах. Для описання атомно-кристалічної структури використовується поняття просторової або кристалічної гратки. Кристалічна гратка (рис. 1.2) являє собою уявну просторову сітку, у вузлах якої розташовуються атоми (іони), що утворюють тверде кристалічне тіло (в даному випадку метал).
Кристалічні просторові гратки, виходячи зі співвідношення між осьовими одиницями і кутами, поділяють на сім систем – сингоній. Позначимо ребра комірки (паралелепіпеда) через а, b і с, а кути між ребрами – через a, b і g. Тоді сім кристалографічних систем відповідають таким формам комірок: 1) триклинна: a ¹ b ¹ c i a ¹ b ¹ g ¹ 90о; 2) моноклінна: a ¹ b ¹ c i a = g = 90о; b ¹ 90о; 3) ромбічна: a ¹ b ¹ c i a = b = g = 90о; 4) гексагональна: a = b ¹ c і a = b = 90о; g = 120о; 5) ромбоедрична: a = b = c і a = b = g ¹ 90о; 6) тетрагональна: a = b ¹ c і a = b = g = 90о; 7) кубічна: a = b = c і a = b = g = 90о; Кристалічні гратки, у яких на одну елементарну комірку припадає один атом, називають простими. Гратки, у яких на одну елементарну комірку припадає декілька атомів, називають складними. Переважна більшість технічно важливих металів утворюють одну з таких високо симетричних складних граток із щільною упаковкою атомів: кубічну об’ємноцентровану (ОЦК), кубічну гранецентровану (ГЦК) та гексагональну. На рис. 1.3 наведені умовно зображені кристалічні гратки і схеми розташування або упаковки атомів (іонів), які дають більш наочне уявлення про кожну із структур. У схемах упаковки атоми (іони) зображені сферами такого розміру, що вони торкаються одна одної. З цього, природно, не варто робити висновок, що ці сфери являють собою нестисливі об'єми, оскільки дуже малі за розмірами ядра атомів оточені електронними оболонками порівняно невисокої густини. Як видно з рис. 1.3, а, в ОЦК гратці атоми розташовані у вузлах комірки й один атом - у центрі об'єму куба. ОЦК гратку мають метали: Rb, К, Na, Li, Tib, Zrb, Tlb, Та, Fea, Mo, W, V, Сг, Ва та ін.
Цей тип гратки мають метали: Саa, Се, Sra, Th, Pb, Ni, Ag, Au, Pd, Pt, Rh, Ir, Feg, Cu та ін. (a, b, g означають, що відповідні метали мають різну кристалічну будову при різних температурах). У гексагональній щільно упакованій (ГЩУ) гратці (рис. 1.3, в) атоми розташовані в кутах і в центрі шестигранних основ призми і три атоми в середній площині призми. Таку упаковку атомів мають метали: Hfa, Mg. Tia, Cd, Re, Os, Ru, Zn, Coa, Be, Tla, Zra і ін. Нарешті, деякі метали (Snb, In), мають тетрагональну гратку. Розміри кристалічної гратки характеризуються періодами (параметрами) а, b, c, під якими розуміють відстань між найближчими паралельними атомними площинами, що утворюють елементарну комірку (рис. 1.3). Період гратки вимірюється в нанометрах (нм) Період гратки металів знаходиться в межах від 0,1 до 0,7 нм. Неважко бачити, що на одну елементарну комірку ОЦК гратки в цілому припадає два атоми: один атом у центрі куба і один атом (за масою) сумарно вносять ті атоми, які розташовуються у вершинах куба (кожен атом у вершині куба одночасно належить восьми сполученим елементарним коміркам і на дану комірку припадає лише 1/8 маси цього атома, а на всю комірку На елементарну комірку ГЦК гратки припадають чотири атоми; із них один атом (за таким же розрахунком, як і для ОЦК гратки) вносять атоми у вершинах куба, а три атоми сумарно (1/2 х 6 = 3) вносять атоми, що знаходяться на середині грані, тому що кожний із таких атомів належить двом граткам. На елементарну комірку ГЩУ гратки припадає шість атомів (3+1/6×12+1/2×2 = 6). Густина кристалічної гратки - об'єму, зайнятого атомами, які умовно можна розглядати як жорсткі кулі (рис. 1.3), характеризується координаційним числом, під яким розуміють число атомів, що знаходяться на рівній і найменшій відстані від даного атома. Чим вище координаційне число, тим більша густина упаковки атомів. У кубічній об’ємноцентрованій елементарній комірці найменша відстань між атомами відповідає
Гранецентрована кубічна і гексагональна щільно-упакована (с/а = 1,633) гратки - найбільш компактні; у них коефіцієнт заповнення об'єму атомами дорівнює 74 %. При зменшенні координаційного числа в гратці Г12 до 6 коефіцієнт заповнення складає близько 50 %, а при координаційному числі 4 - всього біля 25 %. Елементи, що розташовуються в Періодичній системі елементів на границі металів з неметалами (їх називають інколи напівметалами), а також неметали мають більш складні кристалічні гратки з малим координаційним числом. Координаційне число кристалічних структур напівметалевих і неметалевих елементів груп VII, VI, V і частково IV (підгрупи b), може бути визначене за правилом: 8 – N, де N - номер групи Періодичної системи, у якій знаходиться даний елемент. Так, As, Sb, Bi належать до групи V b і за цим правилом мають координаційне число 3. Половину найменшої відстані між центрами атомів називають атомним радіусом. Атомний радіус зростає при зменшенні координаційного числа, оскільки при цьому збільшується простір між атомами. Тому атомні радіуси різних металів звичайно зводяться до К12. Кристалографічні позначення атомних площин Для визначення положення атомних площин (що проходять через атоми) у кристалічних просторових гратках користуються індексами (hkl). Ці індекси являють собою три цілі раціональних числа, які є величинами, оберненими до відрізків осей, що відтинаються даною площиною на осях координат. Одиниці довжини уздовж осей вибирають рівними довжинам ребер елементарної комірки. Наведемо приклади позначення площин. Встановимо спочатку індекси для площини куба. Кожна площина куба (рис. 1.5, а) перетинає тільки одну вісь, при цьому відрізки будуть рівні (1, ∞, ∞); (∞, 1, ∞); (∞, ∞,1). Зворотні розміри відрізків, що відсікаються будуть відповідно рівні: (1, 0, 0); (0, 1, 0); (0, 0, 1). Індекси площини (hkl), які звичайно беруть у дужки, будуть ( У кубічній гратці, крім площин куба (мал. 1.5, а), розрізняють площину октаедра (111), (рис. 1.5, в) та площину ромбічного додекаедра (110) (рис. 1.5, б).
Варто мати на увазі, що індекси характеризують не одну якусь площину, а цілу групу паралельних площин і тоді їх беруть у фігурні дужки. Наприклад, сукупність шести кристалографічних еквівалентностей куба позначають індексами {100}, або {001} і т. д. Сукупність восьми кристалографічних еквівалентних площин октаедра позначають відповідно {111} і т. д.
Рис. 1.5. Індекси кристалографічних площин на напрямків у ОЦК гратці
Індекси напрямку. Для визначення індексів напрямків розташування рядів атомів у кристалічній гратці необхідно із сімейства паралельних площин вибрати напрямок площин, що проходять через початок координат. Далі, прийнявши за одиницю довжину ребра елементарної комірки (або період гратки), визначають координати будь-якої точки цього напрямку. Отримані значення координат точки приводять до відношення трьох найменших цілих чисел. Ці цифри, взяті в квадратні дужки [ u, v, w ], є індексами даного напрямку і всіх паралельних йому напрямків. Основні напрямки в кубічній гратці наведені на рис. 1.5, г. Індекси осей гратки х - [100], y – [101], z - [001]. Індекси просторової діагоналі [111]. Для кубічної гратки індекси напрямку [ uvw ], перпендикулярні до площини (hkl), чисельно рівні індексам цієї площини. Наприклад, індекси вісі х дорівнюють [100], а індекси площини, перпендикулярної до вісі х, дорівнюють (100). Анізотропія властивостей металів. Неважко бачити, що густина розташування атомів в різних площинах (так звана ретикулярна густина) неоднакова. Так, площині (100) в ОЦК гратці належить лише 1 атом (1/4 х 4), площині ромбічного додекаедра (110) – 2 атома: 1 атом вносять атоми, що знаходяться у вершинах (1/4 х 4), і 1 атом в центрі куба. В ГЦК гратці площиною з найбільш щільним розташуванням атомів буде площина октаедра (111), а в ОЦК гратці – площина (110). Внаслідок різної густини атомів у різних площинах i напрямках гратки багато властивостей (хімічні, фізичні, механічні) кожного кристалу залежать від напрямку вирізання зразка по відношенню до напрямків у гратці. Подібна неоднаковість властивостей монокристалу в різних кристалографічних напрямках називається анізотропією. Кристал – тіло анізотропне на відміну від аморфних тіл (скло, пластмаси і ін.), властивості яких не залежать від напрямку. Технічні метали є полікристалами, тобто складаються з великої кількості анізотропних кристалітів. У більшості випадків кристаліти статично невпорядковано орієнтовані один відносно одного; тому у всіх напрямках властивості більш менш однакові, тобто полікристалічне тіло є псевдоізотропним. Така уявна ізотропність металу не буде спостерігатись, якщо кристаліти мають однакову переважну орієнтацію в якихось напрямках. Ця орієнтація або текстура створюється в певній мірі, але не повністю, наприклад, в результаті значної холодної деформації. В цьому випадку полікристалічний метал набуває анізотропії властивостей.
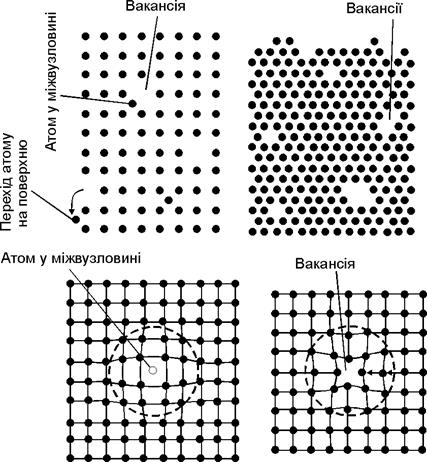
1.3. Дефекти кристалічної гратки металів У будь-якому реальному кристалі завжди є дефекти будови. Дефекти кристалічної будови підрозділяються за геометричними ознаками на точкові (нуль мірні), лінійні (одномірні) та поверхневі (двомірні). Т о ч к о в і д е ф е к т и (рис. 1.6) - малі у всіх трьох вимірах, і розміри їх не перевищують декількох атомних діаметрів. До точкових дефектів відносяться: В кристалі завжди є атоми, кінетична енергія яких є значно вищою від середньої, яка властива для заданої температури нагріву. Такі атоми, особливо ті, що розташовані поблизу поверхні, можуть вийти на поверхню кристалу, а їхнє місце займуть атоми, які знаходились далі від поверхні. Вузли ж, що їм належали, виявляються вільними, тобто виникають теплові вакансії. Джерелами теплових вакансій, тобто вакансій, виникаючих при нагріві, є вільні поверхні, границі зерен, пустоти і тріщини. З підвищенням температури концентрація вакансій зростає. Кількість вакансій при температурі, близької до температури плавлення, може досягати 1 % відносно всього числа атомів у кристалі. Швидким охолодженням від даної температури можна зафіксувати ці вакансії при нормальній температурі (так звані вакансії гартування). Кристал, що знаходиться при даній температурі в термодинамічній рівновазі, має рівноважну концентрацію теплових вакансій. При даній температурі в кристалі утворюються не лише одиночні вакансії (рис. 1.6), але і подвійні, потрійні або їх угрупування. Більшість вакансій є подвійними (так звані дивакансії) (рис. 1.6). Вакансії утворюються не тільки в результаті нагріву, але й у процесі пластичної деформації, рекристалізації, а також при бомбардуванні металу атомами або частками високих енергій (опромінення в циклотроні або нейтронне опромінення в ядерному реакторі). М і ж в у з е л ь н і а т о м и (дефекти Френкеля). Ці дефекти утворюються в результаті переходу атома з вузла гратки в міжвузловину (рис. 1.6). На місці атома, що вийшов із вузла гратки в міжвузловину, утворюється вакансія. У щільно упакованих гратках, характерних для більшості металів, енергія утворення міжвузельних атомів у декілька разів більша від енергії утворення теплових вакансій. Тому в металах дуже важко утворюються міжвузельні атоми й основними точковими дефектами в них є теплові вакансії. Точкові дефекти кристалічної гратки з'являються як результат присутності атомів домішок, які, як правило, є навіть у самому чистому металі. Точкові дефекти викликають локальне спотворення кристалічної гратки Точкові дефекти Шотткі і Френкеля впливають на деякі фізичні властивості металу (електропровідність, магнітні властивості та ін.), а також на фазові перетворення в металах і сплавах.
Рис. 1.6. Точкові дефекти в кристалічній гратці
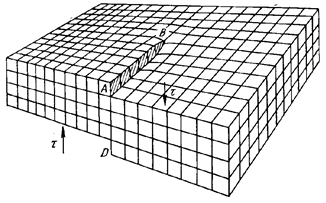
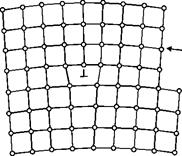
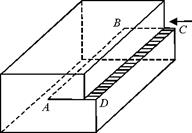
Л і н і й н і д е ф е к т и. Лінійні недосконалості мають малі розміри у двох вимірах і значну протяжність у третьому виміру. Цими недосконалостями можуть бути ряд вакансій чи ряд міжвузельних атомів. Особливим та важливим видом лінійних недосконалостей є дислокації. К р а й о в а д и с л о к а ц і я являє собою локалізоване спотворення кристалічної гратки, викликане наявністю в ній “зайвої” напівплощини або екстра площини. Найбільш простим та наглядним способом введення дислокацій в кристал є зсув. На рис. 1.7 зображений паралелепіпед, верхня частина якого зсунута відносно нижньої на одну міжатомну відстань, причому зафіксовано положення, коли зсув охопив не всю площину ковзання від правої грані паралелепіпеда до лівої, а лише частину площини ковзання. АВСD – ділянка площини ковзання, в якій відбувся зсув; АВ – межа цієї ділянки.
На рис. 1.8 для випадку примітивної кубічної гратки показано розріз паралелепіпеда по атомній площині, перпендикулярній до лінії АВ на рис. 1.7. В цьому перерізі кристал має п вертикальних атомних площин. В результаті показаного на Можна уявити й інший шлях виникнення екстраплощини: подумки розщепити кристал по вертикалі зверху вниз до половини висоти і вставити в нього зверху зайвий атомний шар. Зайвий атомний шар (екстраплощина) діє як клин, вигинаючи гратку навколо свого нижнього краю всередині кристала (див. рис. 1.8). Найбільш істотним є те, що в деякій області безпосередньо поблизу краю екстраплощини всередині кристала гратка сильно перекручена. Вище краю екстраплощини міжатомні відстані менші від нормальних, а нижче краю - більші. Атом на самій кромці екстраплощини має менше сусідів, ніж атом усередині ідеальної гратки. Таким чином, вздовж краю екстраплощини тягнеться область із недосконалою граткою. Область недосконалості кристалу навколо краю екстраплощини і називається крайовою дислокацією. В одному вимірі протяжність цієї недосконалості така ж, як і довжина краю екстраплощини, тобто розмір її макроскопічний. У площині ж, перпендикулярній до краю екстраплощини, область розглянутої недосконалості має малі розміри - від двох до десятьох атомних діаметрів. Отже, крайова дислокація відноситься до класу лінійних недосконалостей. Для наочності можна уявити, що розглянута область недосконалості знаходиться всередині труби, віссю якої є край екстраплощини. Поза цією трубою будова кристала є близькою до ідеальної гратки, а всередині (у так званому ядрі дислокації) - сильно перекручена. Дислокаційні лінії не обриваються всередині кристалу, вони виходять на його поверхню, закінчуються на інших дислокаціях або утворюють замкнуті дислокаційні петлі. Якщо екстраплощина знаходиться у верхній частині кристалу, то дислокацію називають додатною (позитивною)і позначають
Поняття про г в и н т о в у д и с л о к а ц і ю ввів у фізику твердого тіла в 1939 році Бюргерс.
Зробимо в кристалі надріз по площині АВСВ (рис. 1.9, а) і зсунемо праву (передню) частину кристалу вниз на один параметр гратки (рис. 1.9, б). Сходинка, що утворилася при такому зсуві на верхній грані, не проходить через всю ширину кристалу, а закінчується в точці В. Проста кубічна гратка в розглянутому випадку виглядає так, як показано на рис. 1.10. Біля переднього краю кристалу (поблизу точки А) зсув відбувся рівно на один параметр гратки так, що верхня атомна площина справа від точки А зливається в єдине ціле з другою зверху площиною зліва від точки А. Оскільки надріз ABCD дійшов тільки до середини кристалу, то права його частина не може цілком зсунутись відносно лівої на один параметр гратки. Величина зміщення правої частини відносно лівої зменшується в напрямку від точки А до точки В. Верхня атомна площина виявляється вигнутою (рис. 1.10). Точно так же деформується друга
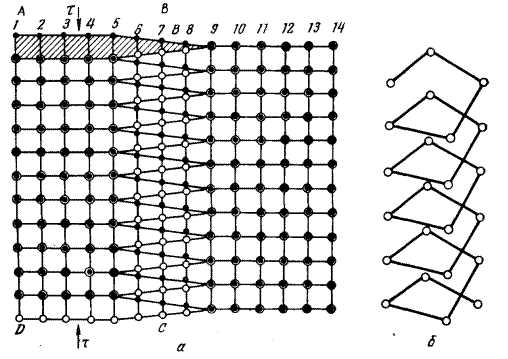
зверху атомна площина; права частина її біля передньої грані кристалу зміщується на один параметр гратки і зливається в єдине ціле з третьою зверху атомною площиною. Ця площина у своїй правій частині зміщується вниз і зливається з четвертою зверху площиною і т.д. Якщо до зсуву кристал складався з паралельних горизонтальних атомних шарів, то після зсуву по площині ABCD він перетворився в одну атомну площину, закручену у вигляді гелікоїди (гвинтових сходів). На рис. 1.11, а показане розташування атомів у двох вертикальних площинах, що проходять безпосередньо по обидва боки від площини зсуву ABCD на рис. 1.9. Якщо дивитися на них з боку правої грані кристалу, то чорні кружки будуть позначати атоми на вертикальній площині зліва від площини зсуву, а світлі кружки - атоми на вертикальній площині справа від площини зсуву. Заштриховано на рисунку сходинку, яка утворилася при зсуві на верхній грані кристалу. На рис. 1.11, а площина ковзання ABCD збігається з площиною рисунка; атоми, позначені чорними кружками, знаходяться під площиною рисунка, а позначені світлими кружками – над нею. Стрілка, яка направлена зверху вниз, позначає напруги зсуву, прикладені до тієї частини кристалу, яка знаходиться над площиною рис. 1.11, а, тобто справа від площини АВСВ на рис. 1.9, б та 1.10. Стрілка, яка направлена знизу вверх, позначає напруги зсуву, прикладені до тієї частини кристалу, яка знаходиться під площиною
Справа від лінії ВС (рис. 1.9, 6), між атомними рядами 9 і 14 (рис. 1.11, а), положення білих і чорних кружків збігаються, тобто відповідні атоми знаходяться на однім горизонті. Та ж картина спостерігається і на деякій відстані зліва від лінії ВС, між атомними рядами 1 і 5. Навколо ж лінії ВС, між атомними рядами 5 і 9, атоми, позначені чорними і білими кружками, тобто ті, що знаходяться під площиною рисунка і над нею, утворюють гвинтову сходинку. Таким чином, після розглянутого зсуву по площині ABCD вдалині від лінії ВС гратка залишається досконалою, а поблизу від лінії ВС вздовж неї тягнеться область недосконалості. У одному вимірі – вздовж лінії ВС область недосконалості має макроскопічний розмір, а в двох інших вона дуже мала (її розміри по нормалі до лінії ВС складають декілька періодів гратки – чотири на рис. 1.11, а). Отже, при зсуві по площині ABCD навколо лінії ВС виникла лінійна недосконалість. Сама ж лінія ВС являє собою границю зони зсуву всередині кристалу, яка відокремлює ту частину площини ковзання, де зсув уже пройшов, від тієї частини, де зсув ще не починався. Отже, згідно даного раніше означення, недосконала область навколо лінії ВС є дислокацією. Оскільки після виникнення такої дислокації в кристалі він складається з атомної площини, закрученої в вигляді гвинтової сходинки, то ця дислокація називається гвинтовою. Точне розташування атомів у ядрі гвинтової дислокації невідоме. Схематично можна собі уявити, що воно є близьким до розташування їх по гвинтовій лінії Дислокація, як і різьба гвинта, може бути правою або лівою. На рис. 1.9 і 1.10 зображені кристали з правою гвинтовою дислокацією: лінію дислокації від верхнього горизонту до нижнього треба обходити по спіралі за годинниковою стрілкою. Якщо ж на рис. 1.9, а зсунути вниз по площині ABCD ліву частину кристалу, то утвориться ліва гвинтова дислокація ВС, яку обійти по спіралі з верхнього горизонту до нижнього можна лише проти годинникової стрілки. Праву дислокацію не можна перетворити в ліву простим перевертанням кристалу (рисунка), як це можна було зробити для перетворення позитивної крайової дислокації в негативну. Права дислокація перетворюється в ліву (і навпаки) лише за допомогою дзеркального відбиття. На відміну від крайової дислокації, яка завжди перпендикулярна до вектора зсуву, гвинтова дислокація паралельна до нього. Друга принципова відмінність гвинтової дислокації від крайової полягає в тому, що крайова дислокація у певній кристалографічній площині може бути утворена зсувом тільки по цій площині. Гвинтова ж дислокація може утворитися при зсуві по будь-якій кристалографічній площині, що містить лінію дислокації, по будь-якій поверхні, що закінчується на цій лінії. Якщо на рис. 1.9, а зробити надріз по площині, що знаходиться під будь-яким кутом до ABCD, але так, щоб цей надріз закінчувався в кристалі на лінії ВС, то після зсуву ми одержимо ту ж саму гвинтову дислокацію ВС. Таким чином, гвинтова дислокація на відміну від крайової не визначає однозначно площину зсуву.
1.4. Аморфні металеві сплави При надвисоких швидкостях охолодження з рідкого стану (~106 К/с) дифузійні процеси настільки сповільнюються, що пригнічується утворення зародків і pіcт кристалів. У цьому випадку при затвердінні утворюється аморфна структура. Матеріали з такою структурою одержали назву аморфні сплави або металеві стекла. Аморфний стан забезпечує металевим матеріалам такі властивості, які значно відрізняються від властивостей відповідних матеріалів з кристалічною структурою. Затвердіння з утворенням аморфної структури принципово можливе практично для всіх металів. На цей час аморфна структура отримана в більш як 20 чистих металах і напівпровідникових матеріалах і більш як у110 сплавах. Це сплави легкоплавких (Pb, Sn, A1 і ін.), рідкісноземельних і перехідних (Fe, Co, Мn, Сг і ін.) металів. Для утворення аморфної структури в перехідних металах до них необхідно добавляти так звані аморфізатори (С, Р, У, N, S і ін.). Існують різні методи отримання аморфних металевих сплавів. Спосіб отримання аморфних металевих сплавів шляхом гартування з рідкого стану (ГРС) є одним з найпоширеніших при їх промисловому виробництві. Фізична суть ГРС полягає в тому, що розплавлений метал тим чи іншим методом “розмазують” в тонкий шар і одній або обом поверхням цього шару забезпечують тепловий контакт з холодильником. За умови незначного термічного опору на поверхні і низької температури та великої теплопровідності холодильника забезпечується значний тепловідвід від розплаву за одиницю часу. Це призводить до того, що швидкості гартування розплаву в випадку тонких шарів можуть досягати 104...1010 К/с. Існує декілька методів ЗРС. Розглянемо деякі з них. 1. Гартування шляхом “пострілу” розплаву. В основуцього методу, застосованого Дювезем, Вілленсом та Клементом в 1959 році, покладено дію ударної хвилі, під впливом якої розплав вистрілюється через невеликий отвір на підкладинку, що охолоджується. Цей метод займає особливе місце серед інших, оскільки він дозволяє досягати найвищих (108...1010 К/с) швидкостей охолодження. Обумовлено це головним чином високою дисперсністю крапель (1...50 мкм) розплаву, які утворюються в процесі його розпилення. За допомогою такого гартування були отримані в аморфному стані деякі чисті елементи, такі як Ge, Te i Ni. При цьому зразки цих елементів були неправильної форми з товщиною на різних ділянках від 0,1 до 100 мкм. Така значна різниця в товщинах дуже ускладнює дослідження фізичних властивостей отриманих зразків. Проте метод гартування “пострілом” розплаву залишається важливим в науковому відношенні, оскільки завдяки високим швидкостям охолодження забезпечує аморфізацію більш широкого класу матеріалів. 2. Метод поршня і ковадла дозволяє отримувати однорідну за товщиною фольгу, що полегшує вимірювання фізичних властивостей загартованих сплавів. Суть методу полягає в тому, що краплі розплаву, які знаходяться в стані вільного падіння потрапляють в щілину між нерухомо закріпленим ковадлом та поршнем, який рухається. Поршень співударяється з ковадлом зі швидкістю 2...5 м/с і розплющує краплю в тонку пластину. Швидкість охолодження розплаву складає при цьому 104...106 К/с. Висока кінетична енергія поршня забезпечує досить щільний контакт розплаву з підкладинкою. Проте при цьому не зовсім зрозуміло, наскільки значною є деформація вже твердого зразка. Вважають, що в першому наближенні вона визначається кінетичною енергією поршня і ступенем перегріву розплаву. Метод поршня і ковадла використовується для виготовлення сплавів на основі тугоплавких металів, наприклад Nb60Rh40, Nb55Ir45, Ta55Rh45,W60Ir20B20 та ін., а також сплавів систем Ni – C, Co – C, Fe – C. 3. Метод спінінгування розплаву. Цей метод використовується, в основному, для отримання неперервних аморфних стрічок. По суті, він є різновидністю запатентованого в 1958 році Пондом методу, в якому вільний струмінь розплавленого металу потрапляє на гартувальну поверхню, що рухається. Але, на відміну від нього, при отриманні АМС методом спінінгування використовується тільки обертовий рух цієї поверхні. Формування стрічки може відбуватись як на зовнішній, так і на внутрішній поверхнях диску, що обертається. При отриманні стрічки гартуванням з рідкого стану на зовнішню поверхню диску (цей спосіб був розроблений Беделлом) шихта сплаву розміщується в кварцовому тиглі і розплавляється за допомогою індуктора. Верхня частина тигля з’єднується з системою подачі інертного газу. Розплав у вигляді тонкого струменя через капіляр видавлюється на гартувальний диск, який обертається зі значною частотою (~ 200...300 с-1). Струмінь розплаву швидко твердіє на кромці диску. Відцентрова сила намагається зіштовхнути стрічку з гартувальної поверхні. В результаті цього утворюється неперервна стрічка товщиною ~ 20...60 мкм. Якість стрічки визначається багатьма факторами: лінійною швидкістю v л диска радіусом R, теплопровідністю матеріалу і ступенем чистоти його обробки, інжекційним тиском р і хімічним складом газу, формою вихідного отвору капіляра, шириною вихідної щілини a n, величиною відстані g між капіляром та ободом, часом контакту розплаву, що охолоджується з поверхнею диска, кутом g зустрічі капіляра з ободом, величиною зміщення l точки дотику розплаву з диском по відношенню до його вісі. Крім вказаних технологічних факторів, важливу роль відіграють також і фізичні фактори: хімічний склад розплаву та його стан, який залежить від часу t і температури перегріву над лінією ліквідусу, значення в’язкості h, поверхневого натягу s н, змочування розплавом матеріалу диска Y. Якщо кількість розплаву досить значна, то в процесі гартування температура диска починає підвищуватись, що впливає на товщину стрічки і умови твердіння розплаву. Для усунення цієї зміни температури використовують охолодження диску і автоматичне регулювання відстані між капіляром та диском з врахуванням коефіцієнта термічного розширення матеріалу диска. При отриманні АМС методом гартування на внутрішню поверхню диска, що обертається, відцентрові сили покращують контакт між зразком і підкладинкою. Це може привести до можливого підвищення швидкості охолодження розплаву. Проте як промисловий метод отримання аморфної стрічки цей метод є менш перспективним. Необхідно зазначити, що при гартуванні розплаву як на зовнішній, так і на внутрішній поверхнях диску, що обертається він охолоджується тільки з одного боку. Основною проблемою при цьому є отримання достатнього ступеня чистоти зовнішньої (вільної) поверхні, яка не контактує з холодильником. Щоб уникнути цього, використовується метод гартування у валках. Метод гартування у валках полягає в тому, що струмінь розплаву спрямовується у вузький проміжок між двома виготовленими зі зміцненої сталі валками, які швидко обертаються. Цей метод дозволяє отримати обидві поверхні АМС задовільної якості, що має важливе значення, наприклад, при виготовленні головок для магнітофонного запису. Але керувати процесом одержання стрічок при використанні цього методу значно складніше, ніж в попередніх. Крім того, хоча процес і характеризується двостороннім охолодженням розплаву, але мала протяжність контакту розплаву з валками призводить до недостатнього зниження температури стрічки в момент її виходу з валків і можливої кристалізації стрічки при охолодженні на повітрі чи в газовому струмені. Одним із шляхів усунення недоліків цього методу і підвищення часу контактув
|



 Жирними лініями на рисунку виділено найменший паралелепіпед, послідовним переміщенням якого у просторі вздовж трьох осей може бути побудована вся гратка. Найменший об'єм кристалу, що дає уявлення про атомну структуру металу у всьому об'ємі, одержав назву елементарної кристалічної комірки.
Жирними лініями на рисунку виділено найменший паралелепіпед, послідовним переміщенням якого у просторі вздовж трьох осей може бути побудована вся гратка. Найменший об'єм кристалу, що дає уявлення про атомну структуру металу у всьому об'ємі, одержав назву елементарної кристалічної комірки. В ГЦК гратці атоми розташовані в кутах куба й у центрі кожної грані (рис. 1.3, б).
В ГЦК гратці атоми розташовані в кутах куба й у центрі кожної грані (рис. 1.3, б). . На цій відстані від даного атома знаходяться 8 сусідів (рис. 1.4, а). Отже, координаційне число для цієї гратки дорівнює 8 і позначається К8. Коефіцієнт заповнення комірки, знайдений як відношення об'єму, зайнятого атомами, до об'єму комірки складає 68 %.
. На цій відстані від даного атома знаходяться 8 сусідів (рис. 1.4, а). Отже, координаційне число для цієї гратки дорівнює 8 і позначається К8. Коефіцієнт заповнення комірки, знайдений як відношення об'єму, зайнятого атомами, до об'єму комірки складає 68 %.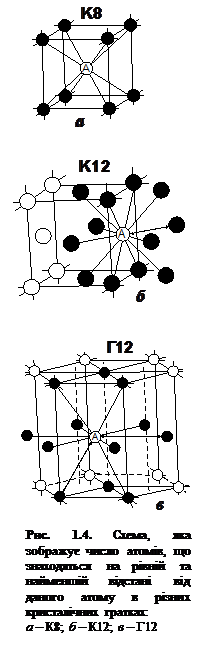 Для гранецентрованої кристалічної комірки координаційне число дорівнює 12 (К12); кожний атом має 12 найближчих сусідів на відстані
Для гранецентрованої кристалічної комірки координаційне число дорівнює 12 (К12); кожний атом має 12 найближчих сусідів на відстані 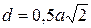 (рис. 1.4, б), що відповідає найбільшій щільності упаковки або укладання у вигляді куль. ГЩУ гратка, для якої с/а = 1,633 має координаційне число 12 (Г12), що також відповідає найбільшій щільності упаковки куль (атомів) (рис. 1.4, в). У багатьох металів, що кристалізуються в гексагональній системі, відношення с/а знаходиться в межах від 1,57 до 1,64, тобто може відхилятися від найщільнішої упаковки, при якій с/а = 1,633. Якщо відношення с/а значно відрізняється від 1,633 (наприклад, для цинку і кадмію), то координаційне число гексагональної гратки відповідає 6.
(рис. 1.4, б), що відповідає найбільшій щільності упаковки або укладання у вигляді куль. ГЩУ гратка, для якої с/а = 1,633 має координаційне число 12 (Г12), що також відповідає найбільшій щільності упаковки куль (атомів) (рис. 1.4, в). У багатьох металів, що кристалізуються в гексагональній системі, відношення с/а знаходиться в межах від 1,57 до 1,64, тобто може відхилятися від найщільнішої упаковки, при якій с/а = 1,633. Якщо відношення с/а значно відрізняється від 1,633 (наприклад, для цинку і кадмію), то координаційне число гексагональної гратки відповідає 6.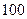 ), (
), ( ), (001), (
), (001), (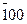 ), (
), ( ), (
), ( ).
).
 , а якщо в нижній - то від’ємною (негативною) і позначають ┬. Різниця між додатною і від’ємною дислокаціями чисто умовна. Перевертаючи кристал, ми можемо перетворити від’ємну дислокацію в додатну. Знак дислокації важливий лише при аналізі їх взаємодії. При прикладенні незначної дотичної напруги дислокації легко переміщуються. В цьому випадку екстраплощина завдяки незначному зсуву перейде в повну площину кристалу, а функції екстраплощини будуть передані до сусідньої площини. Дислокації однакового знаку відштовхуються, а різного знаку взаємно притягуються. Зближення дислокацій різного знаку призводить до їх взаємного знищення (анігіляції).
, а якщо в нижній - то від’ємною (негативною) і позначають ┬. Різниця між додатною і від’ємною дислокаціями чисто умовна. Перевертаючи кристал, ми можемо перетворити від’ємну дислокацію в додатну. Знак дислокації важливий лише при аналізі їх взаємодії. При прикладенні незначної дотичної напруги дислокації легко переміщуються. В цьому випадку екстраплощина завдяки незначному зсуву перейде в повну площину кристалу, а функції екстраплощини будуть передані до сусідньої площини. Дислокації однакового знаку відштовхуються, а різного знаку взаємно притягуються. Зближення дислокацій різного знаку призводить до їх взаємного знищення (анігіляції).