Note that in the case where both players decide to select action A, an outcome that we will note (A,A), the payoff is unknown as a can be any number.
SESS2005
Topics in Microeconomics
Coursework
Arabin Kachakh
Part A 1. Аssume
i) U(x1, x2) = x1 + x2 Budget constraint:
Utility Maximizing Consumption Bundle:
Marginal rate of Transformation (MRT) = Marginal Rate of Substitution (MRS) –utility maximizing condition MRT = - MRS = As MRS is constant, goods
ii) U(
Budget Constraint: maxU(
Utility Maximizing Consumption Bundle: Utility maximizing condition: MRS = MRT MRT = - MRS = As MRT = MRS then - By substituting
Therefore, the optimal bundle (
2. Now assume that the prices change to
i) U (x 1, x 2) = x 1 + x 2
Budget Constraint:
Utility Maximizing Consumption Bundle: MRT=MRS (optimal consumption bundle) MRS = MRT = -
MRS is constant, therefore goods
ii) U (x 1, x 2) = x 1* x 2 Budget Constraint:
10 = 2
Utility Maximizing Consumption Bundle: MRT=MRS MRT= -2
From budget constraint equation we can find out 10 = 2
2
Therefore, (
Consumer is more responsive to the price change in case where MRS = -1, as it is more elastic than in case where MRS = -2
3. What is the general equation for the demand for MRT=-
MRS= -
U(x1, x2) = x1* x2
As MRT=-
- 2
Part B The King of New Landia wants to build a new palace for himself. The estimated cost of which is about £100 million. The project will be financed through taxation. There are 1 million individuals in New Landia and they are all alike. They consume only 2 goods, fruits (f) and nuts (n). They all have the same utility function What will be the impact of each proposal on the people of New Landia? Which option gives them the highest level of utility? How much revenue will each proposal raise? Which option will the King choose? Budget Constraint:
4f+4n=1000 Utility Maximizing Consumption Bundle: MRT = MRS (Optimal Consumption Bundle) MRT = MRS
By substituting it into initial budget constraint we get:
So, the utility function is as follows:
U(f,n)=f (n+2) U(f,n)=126(124+2)=15876 i) By imposing a per unit tax, price for fruits increases by £1, so the new price is
MRT =
MRS=
MRS=MRT
5
Pluging into the budget constraint equation:
4 n +8+4 n =1000 n =124 and f =100.8 Thus, the utility is U(f, n)= f (n +2)=100.8(124+2)=12700.8 Raised revenue will equal to 100.8*1000000=100800000 Due to imposed tax on friuts, the utility will fall from 15876 to 12700.8. This proposal leads to a decrease in fruits consumption. ii) By imposing a per unit tax, price for nuts increases by £1, so the new price is
MRT = -5/4 MRS = - f/n+2 MRT=MRS
Using the same calculations as in previous question we get:
f = Pluging into the budget constraint equation:
n =99, and f =126.25 Thus, the utility in this proposal is U(f, n)= f (n +2)=126.25(99+2)=12751.25 Raised revenue from this proposal equals to 99*1000000=99000000 This proposal leads to a decrease in nuts consumption from 124 to 99 as well as a fall in utility, which decreases from 15876 to 12751.25. However, it increases fruit consumption, increasing it from 126 up to 126.25 iii) Lump-sum tax = £;100 Initial income = £;1000
By imposing a Lump-sum tax, income reduces by £;100, so the new income is £900 A lump-sum tax leads to a new budget constaint: 4 n + 4 f = 900
MRT=MRS MRS=
MRT= -1
Maximised utility is when: 1= f/n +2 f= n+2 Pluging into the budget constraint equation: 4n+4(n+2)=900 n=111.5 f=113.5 Thus, the utility in this proposal is U(f, n)= f (n +2)=113.5(111.5+2)=12882.25 In this case, nuts will be less consumed, it falls from 124 to 111.5, in line with a decrease in fruits consumption which drops from 126 to 113.5. There is a decrese in utility as well, which falls from 15876 to 12882.25. Raised revenue equals to: 100*1000000=100000000 The King of New Landia have a choice of imposing a per unit tax on fruits, on nuts or imposing a lump-sum tax. If he decides to impose a per unit tax of £1 on friuts, he will raise a revenue of £100800000, while imposing a lump-sum tax will raise a revenue of £100000000. Although, a lump-sum tax raises less revenue than a tax on fruits, it is more beneficial for the citizans as it leads to a higher utility and better welfare of the citizens.
Part C
Consider the following game:
Note that in the case where both players decide to select action A, an outcome that we will note (A,A), the payoff is unknown as a can be any number.
|

 =1 and
=1 and  =2, and the consumer has income M = 10. Find the consumer's budget constraint and the utility maximizing consumption bundles for the following utility functions:
=2, and the consumer has income M = 10. Find the consumer's budget constraint and the utility maximizing consumption bundles for the following utility functions: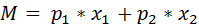
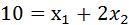
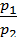 = -
= - 
 =
= 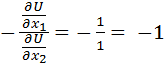
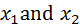 are perfect substitutes. For this reason, consumer chooses to spend all his income on a relatively cheaper good. Therefore, the optimal bundle (
are perfect substitutes. For this reason, consumer chooses to spend all his income on a relatively cheaper good. Therefore, the optimal bundle (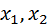 ) = (10,0)
) = (10,0) ,
,  ) =
) = 
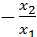
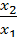 =-
=-  ) = (5, 2,5)
) = (5, 2,5) and
and 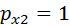 . What is the new utility maximising consumption bundle for each utility function? In which case is the consumer more responsive to the price change?
. What is the new utility maximising consumption bundle for each utility function? In which case is the consumer more responsive to the price change?
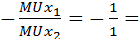 -1
-1 -2
-2


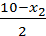
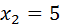
 = 2,5
= 2,5


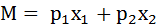
 +
+  =
= 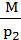
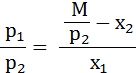
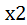 =
= 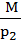
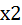 =
= 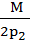
 have the same income,
have the same income,  . The price of fruits and nuts are
. The price of fruits and nuts are  . Three options are being considered to fund the project:
(i) Impose a per unit tax of £1 on fruits
(ii) Impose a per unit tax of £1 on nuts
(iii) Impose a lump-sum tax of £100 on each individual.
. Three options are being considered to fund the project:
(i) Impose a per unit tax of £1 on fruits
(ii) Impose a per unit tax of £1 on nuts
(iii) Impose a lump-sum tax of £100 on each individual.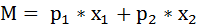
 = -1
= -1  = 1
= 1

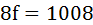


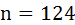
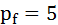 , new budget constraint is as follows:
, new budget constraint is as follows:  = 1000
= 1000 =
= 
 =
= 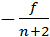
 = 4(
= 4(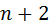 )
)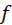 =
= 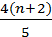
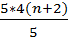 + 4
+ 4  = 1000
= 1000 , new budget constraint is as follows:
, new budget constraint is as follows: 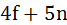 = 1000
= 1000
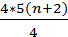 + 5 n = 1000
+ 5 n = 1000




