iii) Can you find the (pure strategy) Nash equilibria of the game as a function of the parameter a?
Nash equilibrium is achieved at the point at which players have no incentive to change their current applied strategy, regardless of whether it is a dominant strategy or not. Therefore, if the other player’s strategy is known, a Nash equilibrium is reached through the implemenation of strategies which do not have a better alternative strategies that could make players relatively better off.
Thus, given the values of outcomes in this game, if the value of a is greater than 1, therefore making the outcome (>1, >1) for (A,A), (A,A) would be the Nash equilibrium as changing the strategy to B would simply make the player’s worse off compared to applying A. Simillarly, for any value of a smaller than 1, (B,B) becomes the Nash equilibrium as changing from strategy B to A would make the players worse off, thus the incentive to do so does not exist.
Accordingly, the Nash equilibrium of the game may be considered as a function, whereby the parameter is a, in which for every value of a that is greater than 1, (A,A) is the pure strategy (Nash equilibria), and for every value of a that is smaller than 1, (B,B) is the Nash equilibrium.
It is important to note here that, if the outcomes of (B,A) and (A,B) were, for instance, (3,0) and (0,3) respectively, than the Nash equilibrium would be different given that the value of a is smaller than 3.
Part D In the consumption/leisure model, let the consumer's utility function be u(L,c)=Lc. Assume that no unearned income is received. Can you show that the daily labour supply curve is l *(w)=12 hours? [That is, this consumer's preferences are such that, regardless of the wage rate, he wants to work exactly half his day.] Consumption and leisure equation: C=(24-L)L C=24w-L*w, where C-consumption, l=leisure, w=wage MRT=MRS(maximised utility) MRT = MRS = - So, MRT=MRS: -w= - C=LW Plug into the cosumption function we get: wL=24w-wL 2Lw=24w So, the daily labour supply: l*(w)=12 hours
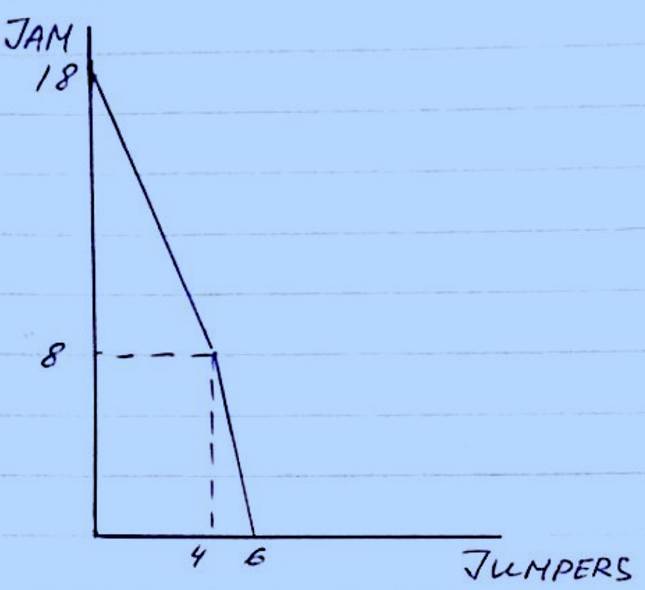
Part E Ada is an expert Jam maker and knitter, her neighbour June also makes jam and knits but she is not as productive as Ada. Indeed, in a day, Ada can make 10 jars of mixed-fruit jam or knit 4 jumpers (or any equivalent linear combination of the two), while June would only make 8 jars or knit 2 jumpers (or any equivalent linear combination of the two). Both produce goods of equivalent quality, only the quantities they are able to produce differ. Ada and June meet once a week and exchange jars of jam for knitwear. Using a graph, illustrate their joint production possibility frontier and explain why Ada can benefit from trading with June. Describe Ada and June's situation in terms of comparative advantage of producing these 2 goods. Given that in a day Ada can make 10 jars of mixed-fruit jam or knit 4 jumpers while June can make 8 jars of jam or knit 2 jumpers. If we assume that they cooperate, or work together, overall they can make 18 mixed-fruit jars or 6 jumpers in a day. Their joint ppf curve has a kink. Production possibility frontier – which shows the maximum combination of two goods that can be produced - of Ada and June (joint PPF) has a kink at the point of 8 jars and 4 jumpers.
MRT (the marginal rate of transformation) illustrates how much more one good can be produced if production of the other is decreased by one. Ada’s MRT =-2.5 June’s MRT= -4 The fact that there is a difference between Ada’s and June’s MRT tells us that they can benefit from exchanging goods between each other. Comparative advantage takes place when a producer manages or has the ability to produce a particular good with a lower cost. By looking at each MRT, we can find out who has a comparative advantage, Ada or June. MRT, in other words, shows how much of one good should be sacrificed in order to produce one more of another good. Ada’s MRT is 2,5, so she would sacrifice 2,5 jars of jam in order to produce one more jumper. However, June’s MRT is 4, which means that she would sacrifice 4 jars of jam in order to produce one more jumper. This means that Ada has a comparative advantage in production of jumpers. However, June has a comparative advantage in production of jam, as she would sacrifice 0.25 jumpers to produce one more jar, while Ada would sacrifice 0.4 jumpers.
Part F The interest rate is 10%. You want to buy a sofa and can either pay £1,000 today or £300 today and £1,000 in 5-year time. Which option do you prefer and why? Does your answer change if the interest rate is in fact 5%? You believe that there is only a 50% chance that your sofa will last you 5 years. Does that change your preferred option?
To answer this question, the present value (PV) should be found out. Present value is the current value of an amount of money in the future When the interest rate is 10%:
With the interest rate of 10%, the more preferable option is to pay £300 now and £1000 in 5 years time, because in this option, the present value, which is 920.9 is less than £1000 When the interest rate is 5%:
PV= 300(today) + In this case, a better option is to pay 1000 now, because the present value to pay £300 now and £1000 in 5 years time is greater than £1000, it is £1083.5 A chance of 50 % that sofa will last only 5 years, does not influence the preferred option, assuming that the customer will anyway pay the same amount of money for the sofa, regardless of what happens to it. But, if there is a condition that if it breaks the customer should not pay the rest of the money, it is better to pay £300 now and £1000 later if the sofa does not break.
Part G In 2008, Joe was a saver. The interest rate was at 4% and his preferences were such that he was saving part of his income every month, thus reducing his present consumption level and increasing his future consumption level. Since 2008, the global economic downturn and the recession in the UK have meant that the interest rate was successively reduced to reach 1% in 2012. Assuming that only the interest rate has changed, is Joe still a saver? Is his present consumption greater or smaller than when the interest rate was higher? Using graphs, explain your answer. The initial interest rate was 4%, however due to the economic downturn the interest rate has fallen down and dropped to 1% by 2012. If we assume that the current consumption (c1) is less than a current income, Joe will gain from the amount he didn’t spend or from the amount he saved. The future consumption (c2) is as follows: (y1 –c1) + r(y1-c1) = y2 + (1+r)(y1-c1), where y1-current income, y2-future income and r=interest rate. It can be seen from the graph that the future consumption decreases as well as a shift in the budget line from L1to L2, due to a fall in the interest rate from 4% to 1%. It can be concluded that the c1 is cheaper than c2 leading to a substitution effect. It is shown by a consumption bundle move from A to B on a graph below. However, Joe’s savings will rise as the income is increased, shown by a movement of the consumption bundle from point B to point C. So, there are two possible options. First, given that an interest rate is decresed, current consumption will be higher in case if substitution effect outweigh income effect as illustrated on the graph. However, if it’s the other way round, income effect>substitution effect, then Joe will save more for the future.
This graph shows that a substitutional effect is larger than income effect. Part H A consumer has set-aside $900 to spend on two goods, X and Y. She likes to consume a unit of good X in combination with a unit of good Y. Any unit of good X that she cannot consume in combination with a unit of good Y is worthless to her, and vice versa. If the price of good X is $10 and the price of good Y is $20, how many units of each good will the consumer purchase? As its known that goods are consumed in combination, it can be deducted that goods X and Y are compliments. Moreover, they are perfect compliments as its given that its worthless to consume one good without the other and vice versa. Consumption of only good X or only good Y is worthless to consumer. So, it won’ t make her better of if she gets an extra consumption of only one good. Since we know that goods are perfect compliments, she will consume exactly the same amount of good X and good Y. So, X=Y Budget constraint: px*x+py*x=900 x=y= Thus, she will buy 30 units of each good.
|

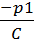 =-w
=-w = -
= - 
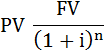
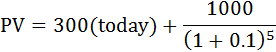
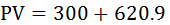 = 920.9
= 920.9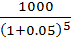 =1083.5
=1083.5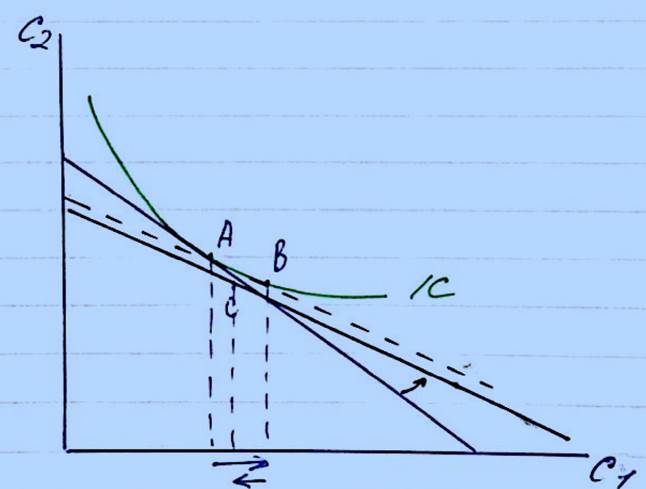
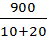 =30
=30


