Видео 1. Измерение расстояний при помощи поперечного масштаба.

 

Различают масштабы крупные и мелкие. Чем меньше знаменатель численного масштаба, тем крупнее масштаб. Даже при идеальном зрении человек не может совместить точку с точкой или штрих с точкой с точностью выше чем 0,1 мм при расстоянии от глаза до бумаги около 25 см, и невозможно определить длину линии на плане точнее, чем 0,1 мм. Поэтому точностью масштаба называется длина горизонтального проложения линии на местности, соответствующей 0,1 мм на плане; т.е. точность масштаба – это точность, с которой можно по карте определить длину линии на местности.

 

Рис. 6. Линейный и поперечный масштабы.

 

 

Картой называют уменьшенное, построенное в картографической проекции, обобщённое изображение поверхности Земли.

 

Для построения карты точки и линии местности проецируют нормалями на поверхность эллипсоида, а затем эту поверхность по определённым законам отображают на плоскость. В отличие от плана, на карте в разных её участках отношение длины отрезка на карте к соответствующему горизонтальному проложению не постоянно: на карте масштаб обобщённый, он может меняться при переходе от участка к участку или при переходе от направления к направлению.

Геодезическим материалом является и профиль местности.

 

Профиль местности – это проекция следа сечения местности вертикальной плоскостью по оси сооружения, т.е. уменьшенное изображение вертикального разреза.

 

Разрез местности, как правило, представляет собой кривую линию, но на профиле её изображают в виде ломаной, где поворотные точки ломаной – характерные точки местности. Для наглядности вертикальные отрезки обычно изображают в более крупном масштабе, чем горизонтальные (как правило, вертикальный масштаб берут в десять раз крупнее горизонтального).

К топографическим материалам предъявляют ряд требований, главными из которых являются точность, наглядность и достоверность. Под точностью понимают соответствие местоположения, очертаний и размеров объектов на планах и картах действительности. Точность передачи количественных характеристик изображённых объектов зависит от масштаба. Зрительное восприятие образа земной поверхности, её характерных черт и особенностей связано с наглядностью планов и карт. Наглядность обусловливается выделением типичных черт местности, определяющих её отличительные особенности, путём обобщений – генерализации, а также применением для изображения земной поверхности топографических условных знаков.

Карты и планы должны быть достоверными, т.е. сведения, составляющие их содержание на определённую дату, должны быть правильными, отвечающими состоянию изображённых на них объектов. Важным элементом достоверности является полнотасодержания, включающая необходимый объём сведений и их разносторонность.

По назначению карты и плана делятся на основные и специализированные. К основным относятся карты и планы общегосударственного картографирования. Эти материалы многоцелевого назначения, поэтому на них отображают все элементы ситуации и рельефа. Специализированные карты и планы создают для решения конкретных задач отдельной отрасли.

 

2.2 Изображение ситуации

 

На картах и планах изображаются различные объекты местности – контуры угодий, постройки, линии дорог, связи и т.д. Совокупность таких объектов называют ситуацией. Эти объекты на картах и планах изображают условными знаками. Если знак с учётом масштаба передаёт реальные размеры объекта, то его называют контурным (площадным, масштабным). К таковым относятся леса, поля, населенные пункты. Внутри охваченной пунктиром территории ставятся условные знаки; они не ставятся только в случае пашни (иногда внутри контура всё-таки ставится буква «п»). С уменьшением масштаба теряется детальность изображения. В этом случае невозможно отобразить объект в реальном масштабе, поэтому используют внемасштабные условные знаки. Так, например, при необходимости изобразить ключ на карте масштаба 1:2000 используется знак диаметром полтора миллиметра, что соответствовало бы в натуре диаметру ключа в более чем два метра (при реальных размерах порядка нескольких сантиметров диаметр знака в масштабе получился бы менее 0,1 мм). При необходимости изобразить такие объекты, у которых в масштабе может быть отображён только один линейный размер (длина дороги, трубопровода, линии электропередач), используют линейные знаки, занимающее, т.о., «промежуточное» положение между площадными и внемасштабными знаками. При необходимости дать характеристику объекта (или указать его название) используют пояснительные знаки, которые представляют собой подписи, позволяющие определить, например, глубину реки, грузоподъёмность моста, породу леса. Специальные условные знаки устанавливают соответствующие ведомства.

 

2.3 Рельеф на картах и планах

 

Совокупность неровностей земной поверхности называют рельефом. На топографических планах и картах рельеф изображают горизонталями.

 

Горизонталь – это линия, соединяющая точки земной поверхности с одинаковыми высотами.

 

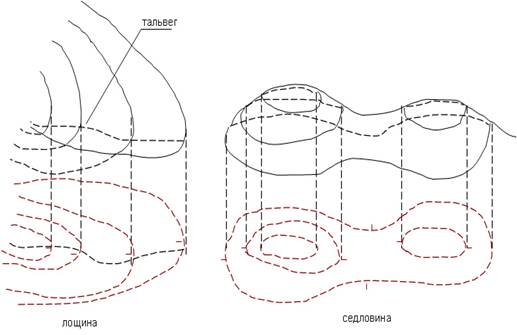
Понятие о горизонтали можно получить, если представить себе местность, затопленную до данной высоты. Береговая линия в этом случае будет горизонталью. Т.о., горизонталь – это след сечения местности уровенной поверхностью. Как правило, выделяют следующие основные формы рельефа (рис. 7). Гора (если высота менее 200 м, то – холм) – это возвышающаяся над окружающей местностью часть земной поверхности. Наивысшая точка горы – вершина, низ – подошва, боковые поверхности – скаты. Для указания направления ската применяют бергштрихи (скатштрихи). Котловина, впадина – замкнутое углубление поверхности. Наиболее низкая часть впадины – дно, линия слияния с окружающей местностью – бровка. Хребет – вытянутая в одном направлении возвышенность со скатами в двух противоположных направлениях. Линия встречи скатов называется водоразделом. Лощина – вытянутое в одном направлении понижение с двумя скатами. Линия встречи скатов называется водосливом. Седловина – понижение между двумя возвышенностями. Наиболее низкую точку между возвышенностями называют перевалом.

 

Рис. 7. Основные формы рельефа.

 

На планах и картах высоты горизонталей изменяются через равные промежутки.

 

Разность высот двух соседних горизонталей называют высотой сечения рельефа, а расстояние между горизонталями по какому-либо направлению на плане – заложением.

 

Высоту сечения рельефа выбирают в зависимости от масштаба карты и характера местности.

О крутизне ската можно судить по величине заложений на карте. Чем меньше заложение, тем круче скат. Для характеристики крутизны ската используют угол наклона ν между линией, соединяющей данные точки и уровенной поверхностью. Чем больше угол наклона, тем круче скат. Другой характеристикой крутизны служит уклон. Уклоном линии местности называют отношение превышения к горизонтальному проложению: i = h/d = tg ν. Уклон – безразмерная величина, его выражают в процентах или в промилле.

 

2.4 Задачи, решаемые на картах и планах при проектировании сооружений

 

При составлении плана землепользования, при проектировании участков, при подготовке вынесения проектов в натуру возникает необходимость вычислять координаты и приращения координат точек местности – необходимость решать прямую и обратную геодезическую задачи. Прямая задача заключается в нахождении координат конечной точки по координатам исходной, длине линии, их соединяющей и дирекционному углу этой линии. Для этого к известным координатам начала отрезка необходимо прибавить приращение координат (ортогональные проекции горизонтального проложения линии на оси координат): x_B = x_A + dcos α, y_B = y_A + d sin α. Обратная задача состоит в нахождении (по известным координатам начала x_A, y_A и концаx_B, y_B) длины горизонтального проложения s и дирекционного угла линии α_AB. По катетам прямоугольного треугольника – приращениям координат Δx_AB = x_A – x_B, Δy_AB = y_A – y_B можно вычислить tg α_AB.= (y_A – y_B)/(x_A – x_B) и, соответственно, сам дирекционный угол α_AB. Вычислив величинуarctg (y_A – y_B)/(x_A – x_B), мы найдём величину румба (острого угла между направлением линии и ближайшим направлением осевого меридана). Чтобы определить его название, достаточно определить знак приращений; если и Δx и Δy положительны, то румб – северо-восточный; если Δx – положителен и Δy – отрицателен, то румб северо-западный; если Δx - отрицательный и Δy – положительный, то румб – юго-восточный; если и Δx и Δy отрицательны, то румб – юго-западный. Зная название и величину румба, легко найти величину дирекционного угла (рис. 8). Зная приращения координат и дирекционный угол, можно найти длину отрезка: s_AB = Δx_AB /cos α_AB = (x_A – x_B)/cos α_AB, s = Δy_AB /sin α_AB = (y_A – y_B)/sin α_AB,

 

 

Рис. 8. Определение дирекционного угла α по величине румба

 

3.1 Единицы мер

 

В повседневной деятельности постоянно приходится сталкиваться с необходимостью измерений. В случае «штучности» объектов достаточно простого счёта, иначе необходимо сравнение с некоторыми заранее определёнными величинами. Такой процесс сравнения называют измерением. Результат измерения – число; таким образом объект получает количественную характеристику.