Расчетно-пояснительная записка
ГРОДНЕНСКИЙ ГОСУДАРСТВЕННЫЙ ПОЛИТЕХНИЧЕСКИЙ КОЛЛЕДЖ
Специальность: _____________________________ _____________________________ _____________________________
КУРСОВАЯ РАБОТА на тему: «Расчет и анализ электрических цепей» Расчетно-пояснительная записка Дисциплина: «Теоретические основы электротехники»
Выполнил: уч. гр. АЭП-22 Король А.Г. Проверил: Гончаров А.А.
Гродно 2011
Введение………………………………………………………………………… 1 Анализ электрического состояния линейных и нелинейных электрических цепей постоянного тока………………………………………. 1.1 Расчет линейных электрических цепей постоянного тока……………. 1.1.1 Применение метода законов Кирхгофа…………………………… 1.1.2 Применение метода контурных токов……………………………. 1.1.3 Применение метода узловых потенциалов...……………............... 1.1.4 Расчет и построение потенциальной диаграммы контура……… 1.2. Расчет нелинейных электрических цепей постоянного тока………… 2 Анализ электрического состояния линейных электрических цепей переменного тока: однофазных и трехфазных ……………………………….. 2.1 Расчет однофазных линейных электрических цепей переменного тока……………………………………………………………. 2.2 Расчет трехфазных линейных электрических цепей переменного тока……………………………………………………………. 3 Исследование переходных процессов в электрических цепях……….. Заключение……………………………………………………………………… Литература……………………………………………………………………….
Электротехника является наукой о техническом использовании электричества и магнетизма в промышленности. Без достаточно глубокого знания электротехники невозможно представить себе инженеров – создателей и руководителей современного производства. Электротехника изучает анализ явлений, происходящих в электрических и магнитных цепях, изучает вопросы, связанные с установившимися и переходными процессами, периодическими несинусоидальными токами в линейных электрических цепях переменного и постоянного тока. Радиотехнические цепи и элементы, используемые для осуществления преобразований сигналов и колебаний, можно разделить на следующие основные классы: линейные цепи с постоянными параметрами, линейные цепи с переменными параметрами, нелинейные цепи. В данной курсовой работе исследуются линейные электрические цепи постоянного и переменного тока с постоянными параметрами, а также нелинейные электрические цепи постоянного тока.
1. АНАЛИЗ ЭЛЕКТРИЧЕСКОГО СОСТОЯНИЯ ЛИНЕЙНЫХ И НЕЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
1.1 Расчет линейных электрических цепей постоянного тока
В электрической цепи, изображенной на рисунке А1 Выполнить следующее: Выполнить следующее: 1) составить на основании законов Кирхгофа систему уравнений для определения токов во всех ветвях схемы; 2) определить токи во всех ветвях схемы, используя метод контурных токов; 3) определить токи во всех ветвях схемы на основании метода наложения; 4) составить баланс мощностей для заданной схемы; 5) результаты расчета токов по пунктам 2 и 3 представить в виде таблицы и сравнить; 6) определить ток во второй ветви методом эквивалентного генератора; 7) построить потенциальную диаграмму для любого замкнутого контура, включающего обе ЭДС.
1.1.1 Применение метода законов Кирхгофа Метод узловых и контурных уравнении основан на применении первого и второго законов Кирхгофа. Он не требует никаких преобразований схемы и пригоден для расчета любой цепи. При расчете данным методом произвольно задаем направление токов в ветвях I1, I2, I3, I4, I5, I6.
Рисунок 1.1 − Схема линейной электрической цепи постоянного тока
Составляем систему уравнений. В системе должно быть столько уравнений, сколько в цепи ветвей (неизвестных токов). В заданной цепи шесть ветвей, значит, в системе должно быть шесть уравнений (m = 6). Сначала составляем уравнения для узлов по первому закону Кирхгофа. Для цепи с n узлами можно составить (n-1) независимых уравнений. В нашей цепи четыре узла (А, В, С, D), значит, число уравнений: n-1 = 4-1 = 3. Составляем два уравнения для любых 3-х узлов, например, для узлов A, В и С. узел A: -I2 – I3 + I4 = 0 узел В: -I1 + I3 + I5 = 0 узел С: I1 – I4 – I6 = 0 Всего в системе должно быть шесть уравнений. Три уже есть. Три недостающих составляем для линейно независимых контуров. Чтобы они были независимыми, в каждый следующий контур надо включить хотя бы одну ветвь, не входящую в предыдущие. Задаемся обходом каждого контура и составляем уравнения по второму закону Кирхгофа. Контур АBCА - обход по часовой стрелке: I1(R1 + r01) + I3R3 + I4R4 = E1 Контур BCDB - обход против часовой стрелки: I1(R1 + r01) + I5R5 + I6R6 = E1 Контур AFCDA - обход против часовой стрелки: I2(R2 + r02) + I4R4 – I6R6 = E2 ЭДС в контуре берется со знаком «+», если направление ЭДС совпадает с обходом контура, если не совпадает – знак «–». Падение напряжения на сопротивлении контура берется со знаком «+», если направление тока в нем совпадает с обходом контура, со знаком «–», если не совпадает.
-I2 – I3 + I4 = 0; -I1 + I3 + I5 = 0; I1 – I4 – I6 = 0; I1(R1 + r01) + I3R3 + I4R4 = E1; I1(R1 + r01) + I5R5 + I6R6 = E1; I2(R2 + r02) + I4R4 – I6R6 = E2. Подставив уравнения, полученные по первому закону Кирхгофа, в последние три мы получим систему из трёх уравнений с тремя неизвестными. Раскроем скобки и приведём подобные слагаемые:
I1(R1 + r01 + R5 + R6) – I3R5 – I4R6 = E1; -I1R6 – I3(R2 + r02) + I4(R2 + r02 + R4 + R6) = E2.
46∙I1 + 32∙I3 + 24∙I4 = 30; 122∙I1 – 61∙I3 – 15∙I4 = 30; -15∙I1 – 54∙I3 + 93∙I4 = 20. Решив данную систему с помощью, определим величину и направление тока во всех ветвях схемы. Вычислим определители Δ, Δ1, Δ2, Δ3.
Вычисляем токи:
Подставив значение токов в первую часть системы, получим:
1.1.2 Применение метода контурных токов Метод контурных токов основан на использовании только второго закона Кирхгофа. Это позволяет уменьшить число уравнений в системе на n-1. Достигается это разделением схемы на ячейки (независимые контуры) и введением для каждого контура-ячейки своего тока – контурного тока, являющегося расчетной величиной. В заданной цепи (рисунок 1.1) можно рассмотреть три контура-ячейки (ABCA, BCDB, AFCDA) и ввести для них контурные токи Ik1, Ik2, Ik3. Контуры-ячейки имеют ветвь, не входящую в другие контуры – это внешние ветви. В этих ветвях контурные токи являются действительными токами ветвей. Ветви, принадлежащие двум смежным контурам, называются смежными ветвями. В них действительный ток равен алгебраической сумме контурных токов смежных контуров, с учетом их направления. При составлении уравнений по второму закону Кирхгофа в левой части равенства алгебраически суммируются ЭДС источников, входящих в контур-ячейку, в правой части равенства алгебраически суммируются напряжения на сопротивлениях, входящих в этот контур, а также учитывается падение напряжения на сопротивлениях смежной ветви, определяемое по контурному току соседнего контура. На основании вышеизложенного порядок расчета цепи методом контурных токов будет следующим: · стрелками указываем выбранные направления контурных токов Ik1, Ik2, Ik3 в контурах-ячейках. Направление обхода контуров принимаем таким же; · составляем уравнения и решаем систему уравнений или методом подстановки, или с помощью определителей.
-Ik1(R1 + r01) + Ik2(R1 + r01 + R5 +R6) – Ik3R6 = -E1 -Ik1R4 – Ik2R6+ Ik3(R2 + r02 + R4 + R6) = -E2
102∙Ik1 – 46∙Ik2 – 24∙Ik3 = 30 -46∙Ik1 + 122∙Ik2 – 15∙Ik3 = -30 -24∙Ik1 – 15∙Ik2 + 93∙Ik3 = -20 Решим систему с помощью определителей. Вычислим определитель системы ∆ и частные определители ∆1, ∆2, ∆3.
Вычисляем контурные токи:
Действительные токи ветвей: I1 = Ik1 – Ik2 = 0.146 – (-0.217) = 0.363 A; I2 = Ik3 = 0.212 A; I3 = Ik1 = 0.146 A; I4 = Ik1 – Ik3 = 0.146 – (-0.212) = 0.358 A; I5 = -Ik2 = 0.217 A; I6 = Ik3 – Ik2 = -0.212 – (-0.217) = 0.005 A. 1.1.3 Применение метода наложения. По методу наложения ток в любом участке цепи рассматривается как алгебраическая сумма частных токов, созданных каждой ЭДС в отдельности. а) Определяем частные токи от ЭДС Е2 при отсутствии ЭДС Е1, т. е. рассчитываем цепь по рисунку 1.2. Решаем задачу методом «свертки». R101 = R1 + r01 = 45 + 1 = 46 Ом В заданной электрической цепи сопротивления R3, R4 и R101 соединены в треугольник, который для упрощения преобразуем в звезду. Определяем сопротивления:
R5B = R5 + RB = 75.431 Ом R6C = R6 + RC = 25.823 Ом
Rэ = R5B6C + RA + R2 = 79.766 Ом Ток источника
Вычисляем остальные токи ветвей:
постоянного тока без источника ЭДС E1
б) Определяем частные токи от ЭДС Е1 при отсутствии ЭДС Е2, т.е. рассчитываем простую цепь по рисунку 1.3. Решаем задачу методом «свертки». R202 = R2 + r02 = 53 + 1 = 54 Ом В заданной электрической цепи сопротивления R3, R4 и R202 соединены в звезду, которую для упрощения преобразуем в треугольник. Определяем сопротивления:
Рисунок 1.3 − Схема линейной электрической цепи постоянного тока без источника ЭДС E2
R5∆16∆2 = R5∆1 + R6∆2 = 57.324 Ом
Rэ = R5∆16∆2∆3 + R1 = 76.556 Ом Ток источника:
Вычисляем остальные токи ветвей:
Вычисляем токи ветвей исходной цепи (рисунок 1.1), выполняя алгебраическое сложение частных токов, учитывая их направление: I1 = -I'1 + I"1 = 0.364 A; I2 = I'2 – I"2 = 0.213 A; I3 = I"3 – I'3 = 0.147 A; I4 = I'4 + I"4 = 0.359 A; I5 = I'5 + I"5 = 0.217 A; I6 = I"6 – I'6 = 0.005 A.
1.1.4 Анализ результатов расчета с помощью баланса мощности Источники E1 и Е2 вырабатывают электрическую энергию, т.к. направление ЭДС и тока в ветвях с источниками совпадают. Баланс мощностей для заданной цепи запишется так: E1∙I1 + E2∙I2 = I12∙(R1 + r01) + I22∙(R2 + r02) + I32∙R3 + I42∙R4 + I52∙R5 + I62∙R6 Подставляем числовые значения и вычисляем 30∙0.363 + 20∙0.212 = 0.3632∙46 + 0.2122∙54 +0.1462∙32 +0.3582∙24 + +0.2172∙61 +0.0052∙15 10.896 + 4.245 = 6.068 + 2.432 + 0.686 + 3.087 + 2.867 + 0.0003 15.141 Вт = 15.140 Вт С учетом погрешности расчетов баланс мощностей получился.
1.1.5 Сравнение результатов расчета методами контурных токов и наложения. Результаты расчета методами контурных токов и наложения сведены в таблицу 1.1. Таблица 1.1
Расчет токов ветвей обоими методами с учетом ошибок вычислений практически одинаков.
Метод эквивалентного генератора используется для исследования работы какого-либо участка в сложной электрической цепи. Для решения задачи методом эквивалентного генератора разделим электрическую цепь на две части: потребитель (исследуемая ветвь с сопротивлением R2, в которой требуется определить величину тока) и эквивалентный генератор (оставшаяся часть цепи, которая для потребителя R2 служит источником электрической энергии, т.е. генератором). Получается схема замещения (рисунок 1.4).
Рисунок 1.4 − Схема замещения
На схеме искомый ток I2 определим по закону Ома для замкнутой цепи:
где Еэ – ЭДС эквивалентного генератора, ее величину определяют как напряжение на зажимах генератора в режиме холостого хода, Eэ = Uхх; rэ – внутреннее сопротивление эквивалентного генератора, его величина рассчитывается как эквивалентное сопротивление пассивного двухполюсника относительно исследуемых зажимов. Изображаем схему эквивалентного генератора в режиме холостого хода (рисунок 1.5), т. е. при отключенном потребителе R2 от зажимов «a» и «б». В этой схеме есть 2 контура, в которых текут токи режима холостого хода. Для нахождения токов Ik1x и Ik2x воспользуемся методом контурных токов. Составим систему уравнений по второму закону Кирхгофа:
-Ik1x∙(R1 + r01) + Ik2x∙(R1 + r01 + R5 + R6) = -E1
Рисунок 1.5 − Схема эквивалентного генератора в режиме холостого хода
102∙Ik1x - 46∙Ik2x = 30 -46∙Ik1x + 122∙Ik3x = -30 Решая данную систему, получаем: Ik1x = 0.221 A, Ik2x = -0.163 A. Зная Ik1x и Ik2x, величины сопротивлений и ЭДС, в схеме можно определить Uxx как разность потенциалов между клеммами «а» и «б». Для этого потенциал точки «б» будем считать известным и вычислим потенциал точки «а». φа = φб + E2 – Ik1x∙R4 – Ik2x∙R6, тогда UXX = φa – φб = E2 – Ik1x∙R4 – Ik2x∙R6 = 20–0.221∙24–(-0.163)∙15 = = 17.142 В. ЕЭ = UXX = 17.142 В. Для расчета внутреннего сопротивл Вычисляем эквивалентное сопротивление схемы (рисунок 1.6) относительно зажимов «а» и «б».
Рисунок 1.6 − Схема пассивного двухполюсника
R101 = R1 + r01 = 45 + 1 = 46 Ом В заданной электрической цепи сопротивления R101, R3 и R5 соединены в звезду, которую для упрощения преобразуем в треугольник. Определяем сопротивления ребер треугольника:
Получаем преобразованную схему с тремя узлами (рисунок 1.7).
Рисунок 1.7 − Схема пассивного двухполюсника с тремя узлами Далее определяем эквивалентное сопротивление цепи:
Зная ЭДС и внутреннее сопротивление эквивалентного генератора, вычисляем ток в исследуемой ветви:
Ток в этой ветви получился практически таким же, как и в пунктах 2 и 3.
1.1.7 Расчет и построение потенциальной диаграммы контура Возьмем контур АBECDFА. Зададимся обходом контура по часовой стрелке. Заземлим одну из точек контура, пусть это будет точка А. Потенциал этой точки равен нулю φА=0 (рисунок 1.1). Зная величину и направление токов ветвей и ЭДС, а также величины сопротивлений, вычислим потенциалы всех точек контура при переходе от элемента к элементу. Начнем обход от точки А. φB = φA – I3∙R3 = -4.685 B φE = φB – I1∙R1 = -21.029 B φC = φE + E1 – I1∙r01 = 8.608 B φD = φC – I6∙R6 = 8.539 B φF = φD + I2∙R2 = 19.788 B φA = φF – E2 + I2∙r02 = 0 B Строим потенциальную диаграмму. По оси абсцисс откладываем сопротивления контура в той последовательности, в которой производим обход контура, прикладывая сопротивления друг к другу, по оси ординат – потенциалы точек с учетом их знака.
включающего обе ЭДС
В электрической цепи, изображенной на рисунке А2, известны сопротивления R1 = 40 Ом, R2 = 22 Ом и входное напряжение U = 60 В. Построить входную вольтамперную Решение: Расчет цепи производим графическим методом. Для этого в общей системе координат строим вольтамперные характеристики (ВАХ) линейных и нелинейных элементов: I = f(U1), I1 = f(U4), I1 = f(U3), I2 = f(U2), I3 = f(U2). ВАХ линейных элементов строим по уравнению Для определения координаты второй точки ВАХ линейного элемента R1 задаемся произвольным значением напряжения. Например, UR = 40 В, тогда соответствующее значение тока Для определения координаты второй точки ВАХ линейного элемента R2 задаемся произвольным значением напряжения. Например, UR = 44 В, тогда соответствующее значение тока
Далее строится общая ВАХ цепи с учетом схемы соединения элементов. В нашей цепи соединение элементов смешанное. Поэтому графически «сворачиваем» цепь. Начинаем с разветвленного участка с линейным элемент Далее мы имеем ветвь с нелинейным элементом нэ13 (I1 = f(U2)), нелинейным нэ2 (I3 = f(U2)) и линейным R2 (I2 = f(U2)), которые соединены параллельно. С учетом этого строим общую для них ВАХ. Для этого задаемся задаемся напряжением и складываем токи при этом напряжении I = I1 + I2 + I3. Проделываем это многократно. По полученным точкам строим ВАХ I = f(U2). Теперь мы имеем характеристики нелинейных элементов нэ123 (I = f(U2)) и нэ1 (I = f(U1)), которые соединены между собой последовательно. Строим для них общую ВАХ. В данном случае задаемся током и складываем напряжения. Проделываем это многократно. По полученным точкам строим общую ВАХ цепи I = f(U). Дальнейший расчет цепи производим по полученным графикам. Чтобы найти токи и напряжения на всех элементах цепи, поступаем так: по оси напряжений находим значение напряжения, равное 60 В (точка «а»). Из этой точки восстанавливаем перпендикуляр до пересечения с общей ВАХ I = f(U), получим точку «b». Из точки «b» опускаем перпендикуляр на ось тока (точка «с»). Отрезок «ос» дает нам искомое значение общего тока I = 1.6 А. Когда опускаем перпендикуляр из точки «b» на ось тока, то пересекаем ВАХ I = f(U1), I = f(U2) в точках «d» и «e» соответственно. Опустив из этих точек перпендикуляры на ось напряжений, получим U1 = 35 B, U2 = 25 B при I = 1.6 A. Когда опускаем перпендикуляр из точки «e» на ось тока, то пересекаем ВАХ I1 = f(U2), I2 = f(U2) и I3 = f(U2) в точках «N», «M» и «P» соответственно. Опуская перпендикуляры из этих точек на ось токов, получим токи I1 = 0.2 A, I2 = 1.1 A, I3 = 0.3 A. Когда опускаем перпендикуляр из точки «N» на ось тока, то пересекаем ВАХ I1 = f(U4) и I1 = f(U3) в точках «K» и «L» соответственно. Опуская перпендикуляры из этих точек на ось напряжения, получим напряжения на каждом участке цепи: U4 = 7 В и U3 = 18 B. В результате имеем следующие значения токов и напряжений на всех элементах цепи: I = 1.6 А; I1 = 0.2 А; I2 = 1.1 A; I3 = 0.3 A; U1 = 35 В; U2 = 25 В; U3 = 7 В; U4 = 18 B.
2.1 Расчет однофазных линейных электрических цепей переменного тока
К зажимам электрической цепи, схема замещения которой приведена на рисунке Б1, подключен источник синусоидального напряжения U = 54∙sin(ωt + 60°) В с частотой f = 50 Гц. Параметры элементов схемы замещения: R1 = 10 Ом, R2 = 20 Ом, L1 = 31.8 мГн, L2 = 50.9 мГн, С1 = 318 мкФ, С2 = 199 мкФ. Выполнить следующее: 1) определить реактивные сопротивления элементов цепи; 2) определить действующие значения токов во всех ветвях цепи; 3) записать уравнение мгновенного значения тока источника; 4) составить баланс активных и реактивных мощностей; 5) построить векторную диаграмму токов, совмещенную с топографической векторной диаграммой напряжений. Решение: 1) Реактивные сопротивления элементов цепи:
Укажем направления токов в ветвях (рисунок 2.1):
Рисунок 2.1 − Схема линейной электрической цепи постоянного тока
Представим схему, приведенную на рисунке 2.1, в следующем виде (рисунок 2.2):
Рисунок 2.2 − Схема замещения линейной электрической цепи постоянного тока
Находим комплексные сопротивления ветвей, затем участков цепи и всей цепи:
Выразим действующее значение напряжений в комплексной форме:
Вычисляем токи ветвей и общий ток цепи:
3) Уравнение мгновенного значения тока источника:
4) Комплексная мощность цепи:
где Sист = 102.21 В∙А, Рист = 72.35 Вт, Qист = 72.2 вар (знак «+» определяет индуктивный характер нагрузки в целом). Активная Рпр, и реактивная Qпр мощности приемников:
Баланс мощностей выполняется: Рист = Рпр; Qист = Qnp 5) Напряжения на элементах схемы замещения цепи: Uab = I·R1 = 26.90 B; Ubc = U234 = 0.06 B; Ucd = I1· XL1 = 26.90 B; Ube = I1·XL2 = 42.90 B; Ued = I1·XC2 = 42.96 B. 6) Строим топографическую векторную диаграмму на комплексной плоскости. Выбираем масштаб: MI = 0.25 А/см, МU = 8 В/см. Определяем длины векторов токов и напряжений:
На комплексной плоскости, и Топографическая векторная диаграмма напряжений характерна тем, что каждой точке диаграммы соответствует определенная точка электрической цепи. Построение векторов напряжений ведем, соблюдая порядок расположения элементов цепи и ориентируя векторы напряжений относительно векторов тока: на активном сопротивлении ток и напряжение совпадают по фазе, на индуктивном элементе напряжение опережает ток на 90°, а на емкостном напряжение отстает от тока на 90°.
на комплексной плоскости
Известно линейное напряжение UЛ = 34 В и сопротивления фаз: RAB = 40 Ом, RBC = 75 Ом, RCA = 50 Ом, XLAB = 60 Ом, XCBC = 25 Ом. Определить полные сопротивления фаз, фазные и линейные токи и ток в нейтральном проводе, активную, реактивную и полную мощности каждой фазы и всей цепи в номинальном режиме и при обрыве провода фазы В. Решение: При соединении трехфазной цепи треугольником расчет будем вести символический методом. 1. Модули фазных напряжений при соединении треугольником равны линейным напряжениям UЛ = UAB = UBC = UCA = 34 В. Комплексы данных напряжений запишем из условия, что вектор
2. Вычислим комплексы фазных сопротивлений: Перед этим найдем реактивные сопротивления элементов цепи.
3. Определяем фазные токи:
4. Находим линейные токи из уравнений, записанных по первому закону Кирхгофа для узлов А, В, С:
5. Вычисляем мощности фаз и всей цепи:
где S = 49.9 B∙A; P = 49.8 Вт; Q = 3.32 вар. 6. Строим в масштабе векторную диаграмму напряжений и токов. Векторы фазных токов
Замыкающие векторные треугольники векторов Выбираем масштаб: MI = 0.25 А/см.
на комплексной плоскости в нормальном режиме
7. При обрыве провода фазы В режим работы фазы СА, включенной между исправными проводами, не изменится (рисунок 2.5). Две другие фазы окажутся включенными последовательно на линейное напряжение UCA. Трехфазная цепь превращается в однофазную цепь с двумя параллельными ветвями. Найдем теперь значения для образовавшейся фазы СВА, полученной из последовательно включенных фазных цепей АВ и ВС, включенной под линейное напряжение UCA параллельно фазе СА. По закону Ома посчитаем действующее значение силы тока, а также полное сопротивление в фазе СВА:
Рисунок 2.5 − Схема трехфазной линейной электрической цепи переменного тока при обрыве фазного провода
Так как токи в линейных проводах А и С равны, то найдем их значение:
Определим значения напряжений на участках АВ и ВС:
8. Вычисляем мощности фаз и всей цепи:
где S = 29.1 B∙A; P = 28.4 Вт; Q = -6.3 вар. 9. Строим в масштабе векторную диаграмму напряжений и токов. Векторы фазных токов
Замыкающие векторные треугольники векторов Выбираем масштаб: MI = 0.25 А/см.
на комплексной плоскости при обрыве фазного провода
Определить закон изменения тока и ЭДС самоиндукции в цепи. Определить практическую длительность переходного процесса и энергию магнитного поля при t = 3τ.. Схема цепи приведена на рисунке Б3.
|

 Содержание
Содержание
 , известны сопротивления приемников R1=45 Ом, R2=53 Ом, R3=32 Ом, R4=24 Ом, R5=61 Ом, R6=15 Ом, сопротивления источников ЭДС r01=1 Ом, r02=1 Ом и значения ЭДС E1=30 В, Е2=20 В.
, известны сопротивления приемников R1=45 Ом, R2=53 Ом, R3=32 Ом, R4=24 Ом, R5=61 Ом, R6=15 Ом, сопротивления источников ЭДС r01=1 Ом, r02=1 Ом и значения ЭДС E1=30 В, Е2=20 В.
 Мы получили систему из шести уравнений с шестью неизвестными:
Мы получили систему из шести уравнений с шестью неизвестными: I1(R1 + r01) + I3R3 + I4R4 = E1;
I1(R1 + r01) + I3R3 + I4R4 = E1; Подставим численные значения ЭДС источников и сопротивлений:
Подставим численные значения ЭДС источников и сопротивлений:









 Подставляем в уравнение численные значения ЭДС и сопро
Подставляем в уравнение численные значения ЭДС и сопро  ;
;  ;
; ;
; 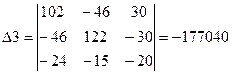 .
. A;
A;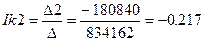 A;
A; A.
A. Ом
Ом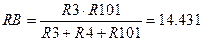 Ом
Ом Ом
Ом Ом
Ом А
А А
А А
А А
А А
А  А
А Ом
Ом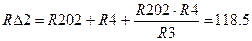 Ом
Ом Ом
Ом Ом
Ом Ом
Ом Ом
Ом А
А А
А  А
А А
А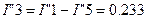 А
А А
А 
 Ik1x∙(R1 + r01 + R3+ R4) – Ik2x∙(R1 + r01) = E1
Ik1x∙(R1 + r01 + R3+ R4) – Ik2x∙(R1 + r01) = E1 Подставляем численные значения параметров в систему:
Подставляем численные значения параметров в систему: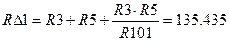 Ом
Ом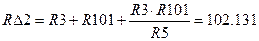 Ом
Ом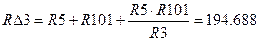 Ом
Ом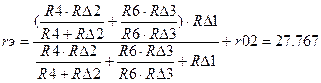 Ом
Ом А
А характеристику схемы. Определить токи во всех ветвях схемы и напряжения на отдельных элементах, используя полученные вольтамперные характеристики.
характеристику схемы. Определить токи во всех ветвях схемы и напряжения на отдельных элементах, используя полученные вольтамперные характеристики. . Она представляет собой прямую, проходящую через начало координат.
. Она представляет собой прямую, проходящую через начало координат.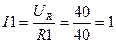 A. Соединив полученную точку с началом координат, получим ВАХ линейного элемента.
A. Соединив полученную точку с началом координат, получим ВАХ линейного элемента. A. Соединив полученную точку с началом координат, получим ВАХ линейного элемента
A. Соединив полученную точку с началом координат, получим ВАХ линейного элемента ом R1 и нелинейным элементом нэ3. Они соединены последовательно, их ВАХ I1 = f(U4) и I1 = f(U3). С учетом этого строим общую для них ВАХ. Для этого задаемся задаемся током и складываем напряжения при этом токе U2 = U4 + U3. Точка пересечения этих значений тока и напряжения дает одну из точек их общей ВАХ. В результате получаем множество точек и по ним строим ВАХ I1 = f(U2).
ом R1 и нелинейным элементом нэ3. Они соединены последовательно, их ВАХ I1 = f(U4) и I1 = f(U3). С учетом этого строим общую для них ВАХ. Для этого задаемся задаемся током и складываем напряжения при этом токе U2 = U4 + U3. Точка пересечения этих значений тока и напряжения дает одну из точек их общей ВАХ. В результате получаем множество точек и по ним строим ВАХ I1 = f(U2).
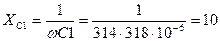 Ом
Ом Ом
Ом Ом
Ом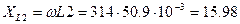 Ом
Ом 2) Расчет токов в ветвях цепи выполняем методом эквивалентных преобразований.
2) Расчет токов в ветвях цепи выполняем методом эквивалентных преобразований. Ом
Ом Ом
Ом Ом
Ом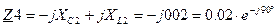 Ом
Ом Ом
Ом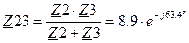 Ом
Ом Ом
Ом Ом
Ом В.
В. 
 А
А В
В А
А А
А А
А
 А
А В∙А
В∙А Вт
Вт вар
вар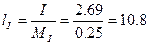 см;
см;  см;
см; см;
см;  см;
см; см;
см;  см;
см; см;
см; 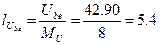 см;
см; см;
см;  см.
см.
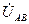 совмещен с действительной осью комплексной плоскости,
совмещен с действительной осью комплексной плоскости, В;
В; В;
В;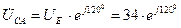 В;
В; Ом
Ом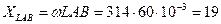 Ом
Ом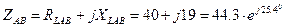 Ом,
Ом, Ом,
Ом, Ом,
Ом, A,
A, A,
A, A,
A,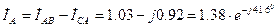 A;
A; A;
A; A;
A; В∙А,
В∙А,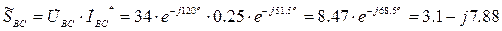 В∙А,
В∙А, В∙А,
В∙А, B∙A,
B∙A,
 ,
,  ,
,  строятся под углами ψАB, ψBC, ψCA к действительной оси. К концам векторов
строятся под углами ψАB, ψBC, ψCA к действительной оси. К концам векторов  ,
, 


 см;
см;  см;
см;  см;
см;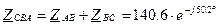 Ом
Ом A,
A, A,
A, A,
A,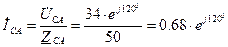 A,
A, A,
A,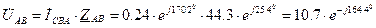 A,
A,  A
A В∙А,
В∙А, В∙А,
В∙А, В∙А,
В∙А,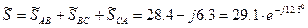 B∙A,
B∙A, см;
см; см;
см; см;
см; Электрическая цепь содержит катушку с сопротивлением R = 50 Ом и индуктивностью L = 0.5 Гн, напряжение источника питания U = 110 В.
Электрическая цепь содержит катушку с сопротивлением R = 50 Ом и индуктивностью L = 0.5 Гн, напряжение источника питания U = 110 В.


