Принцип оптимальности Беллмана, уравнение Беллмана

Принцип оптимальности Беллмана. Еще раз подчеркнем, что смысл подхода, реализуемого в динамическом программировании, заключен в замене решения исходной многомерной задачи последовательностью задач меньшей размерности.

Перечислим основные требования к задачам, выполнение которых позволяет применить данный подход:

Ø объектом исследования должна служить управляемая система (объект) с заданными допустимыми состояниями и допустимыми управлениями;

Ø задача должна позволять интерпретацию как многошаговый процесс, каждый шаг которого состоит из принятия решения о выборе одного из допустимых управлений, приводящих к изменению состояния системы;

Ø задача не должна зависеть от количества шагов и быть определенной на каждом из них;

Ø состояние системы на каждом шаге должно описываться одинаковым (по составу) набором параметров;

Ø последующее состояние, в котором оказывается система после выбора решения на k-м. шаге, зависит только от данного решения и исходного состояния к началу k-го шага. Данное свойство является основным с точки зрения идеологии динамического программирования и называется отсутствием последействия.

Рассмотрим вопросы применения модели динамического программирования в обобщенном виде. Пусть стоит задача управления некоторым абстрактным объектом, который может пребывать в различных состояниях. Текущее состояние объекта отождествляется с некоторым набором параметров, обозначаемым в дальнейшем ξ и именуемый вектором состояния. Предполагается, что задано множество Ξ всех возможных состояний. Для объекта определено также множество допустимых управлений (управляющих воздействий) X, которое, не умаляя общности, можно считать числовым множеством. Управляющие воздействия могут осуществляться в дискретные моменты времени k(k∊1:n), причем управленческое решение заключается в выборе одного из управлений xk∊Х. Планом задачи или стратегией управления называется вектор х = (х1, х2,.., xn-1), компонентами которого служат управления, выбранные на каждом шаге процесса. Ввиду предполагаемого отсутствия последействия между каждыми двумя последовательными состояниями объекта ξk и ξk+1 существует известная функциональная зависимость, включающая также выбранное управление: ξk+1 = φk(xk, ξk), k∊1:п-1. Тем самым задание начального состояния объекта ξ1∊Ξ и выбор плана х однозначно определяют траекторию поведения объекта, как это показано на рис. 5.1.

Эффективность управления на каждом шаге k зависит от текущего состояния ξk, выбранного управления xk и количественно оценивается с помощью функций fk(хk, ξk), являющихся слагаемыми аддитивной целевой функции, характеризующей общую эффективность управления объектом. (Отметим, что в определение функции fk(хk, ξk) включается область допустимых значений хk, и эта область, как правило, зависит от текущего состояния ξk.) Оптимальное управление, при заданном начальном состоянии ξ1, сводится к выбору такого оптимального плана х*, при котором достигается максимум суммы значений fk на соответствующей траектории.

Так, если система в начале k - шага находится в состоянии и мы выбираем произвольное управление , то она придет в новое состояние в 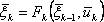, и последующие управления должны выбираться оптимальными относительно состояния . Последнее, означает, что этих управлениях максимизируется величина , то есть показатель эффективности на последующих до конца процесса шагах обозначим через .

Выбрав оптимальное управление на оставшихся шагах, получим величину , которая зависит только от , то есть .

Назовем величину условным максимумом. Если мы теперь выберем на k-м шаге некоторое произвольное управление , то система придет в состояние . Согласно принципу оптимальности, необходимо выбирать управление 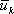так, чтобы оно в совокупности с оптимальным управлением на последующих шагах (начиная с (k+1)-го) приводило бы к общему показателю эффективности на шагах, начиная с k-uго и до конца. Это положение в аналитической форме можно записать в виде следующего соотношения:

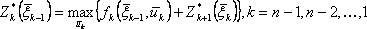(1)

получившего название основного функционального уравнения динамического программирования, или основного рекуррентного уравнения Беллмана.

Решая уравнение (1) для определения условного максимума показателя эффективности шагов, начиная с k-го, мы определяем соответствующее оптимальное управление , при котором этот максимум достигается. Это управление также зависит от ; будем обозначать его через и называть условным оптимальным управлением на k-м шаге. Основное значение уравнения (1), в котором реализована идея динамического программирования, заключается в том, что решение исходной задачи определения максимума функции n переменных сводится к решению последовательности n задач, задаваемых соотношениями (1), каждое из которых является задачей максимизации функции одной переменной .