Дифференцирующие звенья в моделях приводов
Блок дифференцирования – один из наиболее распространенных в моделях автоматических систем. В приводах таким блоком является тахогенератор, если под входной координатой понимается угол поворота его вала. Моделирование же процедуры чистого дифференцирования является наиболее проблематичной. Среди всех математических операций дифференцирование воспроизводится с наименьшей точностью. В моделях, отображающих процессы в реальном времени, например в виртуальных осциллографах используются алгоритмы решения разностных уравнений, дающих вполне удовлетворительные результаты. Для получения частотных характеристик блок идеального дифференцирования заменяется реальным дифференцирующим звеном вида:
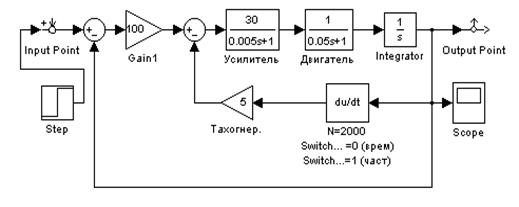
Точность тем выше, чем больше N. В MatLab этот блок вызывается из библиотеки Simulink Extras > Linearisation и установкой параметра Switch value в 0 или 1 может переключаться для отображения соответственно временных или частотных характеристик. Рассмотрим типичную структурную схему силового привода, содержащую исполнительный двигатель, усилитель и тахогенератор, включенный в контур местной обратной связи (параллельная коррекция). Это наиболее распространенный способ улучшения динамических свойств силовых приводов. Численные параметры реальной замкнутой системы приведены на рисунке 3.4, а на рисунках 3.5а и 3.5б – переходные процессы при разных способах реализации алгоритма блока дифференцирования. Неустойчивость в последнем случае говорит об ошибочности модели. Ошибка возможна при выборе числа N на основании распространенного правила – влияние второстепенных факторов должно быть на порядок меньше основных. При N=2000 постоянная времени в (3.2) будет составлять 0,0005 с., то есть 1/10 от наименьшей постоянной времени исследуемой системы (усилителя). Однако близкое расположение фазовой характеристики к
Рис. 3.4. Модель замкнутой системы с обратной связью по углу поворота
а б
3.5. Переходные процессы при различных способах реализации блока дифференцирования
Однако в модели не всегда удается избавиться от дифференцирующих звеньев. Это касается, например кинематической цепи на рисунке 1.5. В этих случаях к исследованию частотных характеристик можно приступать после совпадения результатов моделирования во временной и частотной областях.
Рис. 3.6. Модель системы с обратной связью по скорости
Приведенные примеры показывают, что именно детальный анализ процесса моделирования помогает избежать ошибок. Многообразие же решаемых задач не избавляет практически ни одно развивающееся программное средство от недоработок. Их выявление и устранение – естественный процесс.
|

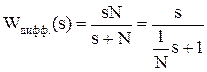 . (3.2)
. (3.2) в области частоты среза исходной системы может сделать её неустойчивой при добавлении любого динамического звена, что и происходит в данном случае. Нужно либо увеличить N, либо изменить модель. В данном случае дифференцирующее звено можно вообще исключить из модели, что обычно и делается. Вводится обратная связь не по углу, а по скорости, как показано на рисунке 3.6.
в области частоты среза исходной системы может сделать её неустойчивой при добавлении любого динамического звена, что и происходит в данном случае. Нужно либо увеличить N, либо изменить модель. В данном случае дифференцирующее звено можно вообще исключить из модели, что обычно и делается. Вводится обратная связь не по углу, а по скорости, как показано на рисунке 3.6.