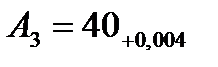МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ.
Прямая задача
Для обеспечения полной взаимозаменяемости расчет ведем по методу максимума-минимума, при котором допуск замыкающего размера определяется арифметическим путем допусков и предельных размеров. Этот метод учитывает только предельные отклонения звеньев и их самые неблагоприятные сочетания. а) метод максимума-минимума N= N= 88-(20+3+60+3) = 2 N=
Следовательно TN=(0,3)+(0,05+0,05)+(0,15)+(0,05+0,05)+(0,3)= =0,95
N – номинальный размер, который определяется из формулы (4.24). Для определения верхнего и нижнего отклонения удобно использовать следующие формулы:
ES (N) = EI (N) =
ES (N) = 0-(-0,3-0,05-0-0,05) = 0,4
EI (N) = - 0,3-(0+0,05+0,15+0,05) = - 0,55
TN = ES (N) - EI (N) = 0,4-(-0,55) = 0,95
Следовательно: N=
б) теоретико-вероятностный метод TN’ =
TN’ = Найдем погрешность:
ES(N) = -0,075+ EI(N) = -0,075- Следовательно: N=
Обратная задача
Способ равноточных допусков (метод одного класса точности). Условно принимаем, что возрастание линейного размера допуска имеет ту же закономерность, что и возрастание допуска диаметра, а именно для 5-17 квалитетов. i = 0,45 Номинальные верхние отклонения единичного допуска см. в таблице 4.2. Таблица 4.2. Номинальные верхние отклонения единичного допуска
Таким образом, в общем виде
Значения i для основных интервалов в диапазоне до 400 мм приведены в таблице4.3. Таблица 4.3 Значения i для основных интервалов в диапазоне до 400 мм
TN = TN = Откуда находим, что N =
Для Назначим отклонения всех составляющих охватываемых размеров с “ минусом ” (как для основного вала) и определим отклонения охватывающего размера
Причем разницу в 160 мкм вносим в допуск на Далее по формулам (4.25) и (4.26) найдем отклонения для 200 = -200 = Получили, что Таблица 4.4 Таблица результатов вычислений.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
|



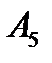
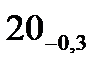

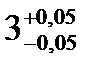

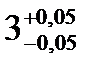


 - (
- ( ,
, 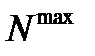 =
= 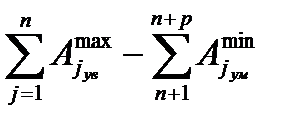
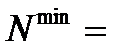

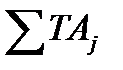 – допуск замыкающего размера равен сумме допусков составляющих размеров.
– допуск замыкающего размера равен сумме допусков составляющих размеров. - верхнее отклонение
- верхнее отклонение - нижнее отклонение
- нижнее отклонение
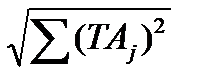
 0,73
0,73 %
% 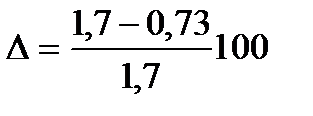 % = 57%
% = 57%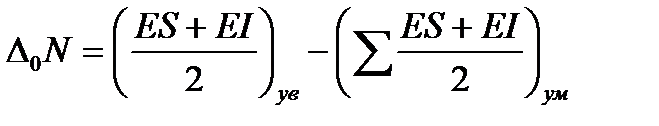

 -0,075
-0,075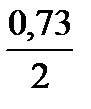 = 0,29 - верхнее отклонение
= 0,29 - верхнее отклонение = -0,44 - нижнее отклонение
= -0,44 - нижнее отклонение
 + 0,001D – величина номинального допуска, где D в (мм), i в (мкм).
+ 0,001D – величина номинального допуска, где D в (мм), i в (мкм).
 , где
, где 

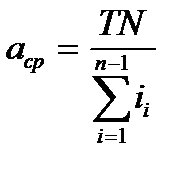 . Эта величина определяет по какому квалитету нужно обрабатывать деталь.
. Эта величина определяет по какому квалитету нужно обрабатывать деталь. = 71, поэтому выбираем 11 квалитет с единичным допуском 100.
= 71, поэтому выбираем 11 квалитет с единичным допуском 100.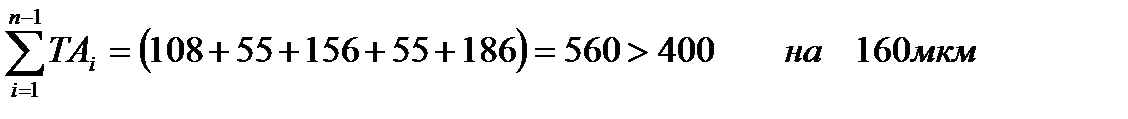
 (4.25)
(4.25) (4.26)
(4.26) =40, как на самый большой номинальный из охватываемых размеров, т.е. получим
=40, как на самый большой номинальный из охватываемых размеров, т.е. получим 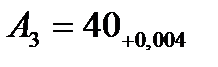 .
. - (-
- (-  ),
), 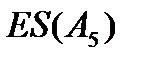 =200-218= –18
=200-218= –18 - 0,
- 0,  = – 200
= – 200
 ном., мм
ном., мм
 , мкм
, мкм
 , мм
, мм