Фундаментальные геодезические постоянные.
Фигура и гравитационное поле Земли тесно взаимосвязаны и их изучение представляет собой по существу одну задачу. Сложная структура гравитационного поля, обусловленная неправильностями фигуры Земли и особенностями распределения плотностей масс, создает значительные трудности при определении потенциала силы тяжести W. Задача определения потенциала Wсущественно облегчается, если гравитационное поле Земли представить в виде двух полей: основного, или нормального и остаточного, или аномального и каждое из них изучать отдельно.
За физическую модель Земли при этом принимают так называемый уровенный эллипсоид вращения, внешняя поверхность которого является уровенной и сила тяжести в каждой точке ее направлена по нормали к ней.
Центр уровенного эллипсоида совмещают с центром масс Земли, а ось его вращения — с осью вращения Земли. Гравитационное поле, создаваемое уровенным эллипсоидом на его поверхности и во внешнем пространстве, называют нормальным гравитационным полем, а силу тяжести — нормальной и обозначают буквой у.
Определив параметры уровенного эллипсоида, можно вычислить нормальный потенциал Uи другие элементы нормального поля силы тяжести на его поверхности и во внешнем пространстве. Приняв поверхность уровенного эллипсоида за отсчетную, задачу изучения фигуры Земли можно свести к определению отклонений ее физической поверхности от поверхности эллипсоида, а задачу определения потенциала Wреальной силы тяжести к определению небольших разностей T=W—U, называемых возмущающим потенциалом Земли в точках земной поверхности.
Уровенный эллипсоид, принимаемый за физическую модель Земли при определении ее фигуры и гравитационного поля, принято называть Нормальной Землей. При решении ряда задач геодезии, геофизики и небесной механики широкое распространение получило представление потенциала Vпритяжения Земли (включая ее атмосферу) в виде разложения в ряд шаровых функций геоцентрических координат г, Ф и L, т. е. геоцентрических радиуса, широты и долготы соответственно. Потенциал притяжения VoНормальной Земли (уровенного эллипсоида) имеет вид:
(1.12)
где индексом «О» отмечены параметры Нормальной Земли; f — универсальная гравитационная постоянная; Мо — масса уровенного эллипсоида; r— геоцентрический радиус-вектор точек его поверхности; а — большая полуось эллипсоида; /гп0 — зональные гармонические коэффициенты второй степени при полиномах Лежандра Р2п (sin Ф).
Параметры Нормальной Земли в зависимости от их величины и важности классифицируют следующим образом.
Параметры нулевого порядка: геоцентрическая гравитационная постоянная fM; нормальный потенциал силы тяжести на поверхности Нормальной Земли U0; экваториальный радиус Земли а; нормальная сила тяжести на экваторе.
Параметры, порядка сжатия: нормальный гармонический коэффициент геопотенциала второй степени J2; геометрическое сжатие Земли а=(а—b)/а; гравиметрическое сжатие Земли P=(, где р — нормальная сила тяжести на полюсе; малые параметры, являющиеся функцией угловой скорости вращения Земли со, и параметры нулевого порядка, а именно:
Параметры высших порядков: коэффициент 1 в формуле нормальной силы тяжести; гармонические коэффициенты нормального потенциала притяжения J4°, Jв0,... и т. д. Фундаментальные геодезические постоянные
Из-за особой важности некоторые параметры Нормальной Земли получили название фундаментальных геодезических постоянных, К ним в настоящее время относят следующие величины: fM, а, J2,, где — угловая скорость вращения Земли. Другие параметры Нормальной Земли являются производными постоянными. Их можно получить, используя известные соотношения между различными параметрами.
К числу фундаментальных постоянных относят также: скорость света в вакууме с, геоцентрическую гравитационную постоянную для атмосферы fMAи универсальную гравитационную постоянную f.
Фундаментальные геодезические постоянные определяют, используя результаты наблюдений ИСЗ, далеких КЛА, а также результаты астрометрических и гравиметрических измерений.
Параметры Нормальной Земли определяют, соблюдая следующие условия:
1) центр уровенного эллипсоида вращения должен совпадать с центром масс Земли, а его главная ось инерции, являющаяся осью его вращения, — с осью вращения Земли;
2) угловые скорости со вращения уровенного эллипсоида и реальной Земли должны быть одинаковыми;
3) масса Мо уровенного эллипсоида должна быть равна массе М реальной Земли (fMo=fM);
4) зональные гармонические коэффициенты геопотенциала второй степени для уровенного эллипсоида J2° и реальной Земли /г должны совпадать;
5) нормальный потенциал Uoсилы тяжести на поверхности уровенного эллипсоида должен быть равен реальному потенциалу силы тяжести Woна поверхности геоида.
При решении ряда задач геодезии вместо Uoв число фундаментальных геодезических постоянных включают большую полуось а уровенного эллипсоида. Тогда пятое условие формулируют иначе: большая полуось а уровенного эллипсоида должна быть подобрана таким образом, чтобы его объем равнялся объему геоида.
С течением времени по мере накопления измерительной информации фундаментальные геодезические постоянные постепенно уточняются. В соответствии с рекомендациями XVII Генеральной ассамблеи Международного геодезического и геофизического союза (МГГС) и входящей в него Международной ассоциации геодезии (МАГ), состоявшейся в Канберре (Австралия, 1979 г.), приняты следующие значения фундаментальных геодезических постоянных:
fM= (3 896005±0,5) · 108 м3с-2;
J2 = (108263±0,5)10-8;
а = 6378137±2 м;
w = 7 292 115-Ю-11 рад-с"1.
Эти постоянные являются исходными для принятой геодезической референц-системы 1980 г.
Зная фундаментальные геодезические постоянные, можно вычислить другие параметры Нормальной Земли по точным формулам. Приведем некоторые формулы, устанавливающие связи между разными параметрами Нормальной Земли с точностью до малых величин второго порядка, что вполне достаточно для решения многих задач высшей геодезии на современном этапе.
Сжатие Земли а связано с параметрами /2и g формулой
где <7 определяется по формуле (1.14).
Нормальный потенциал Uoна поверхности уровенного эллипсоида равен
Масса эллипсоида Мо и нормальная сила тяжести на экваторе уе связаны соотношением
Нормальная сила тяжести у0 на поверхности уровенного эллипсоида на широтах В может быть вычислена по формуле
где
Нормальную силу тяжести у (мГал) во внешнем пространстве находят по формуле
где Н — высота над эллипсоидом, м.
Приведенным выше фундаментальным геодезическим постоянным соответствуют следующие значения полярного сжатия Земли а и нормальной силы тяжести уе на экваторе уровенного эллипсоида:
а = 1:298,257 ± 0,001; уe = 978 033 ± 1 мГал.
|

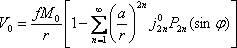
 (1.13)
(1.13) (1.14)
(1.14)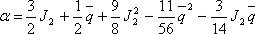 (1.14)
(1.14)

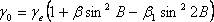 (1.15)
(1.15) (1.16)
(1.16)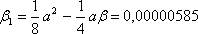 (1.17)
(1.17) (1.18)
(1.18)


