Числа Рамсея.
Теорема Рамсея гарантирует существование чисел Рамсея для любых k и m. Таким образом можно говорить о содержании в бесконечном графе высокоорганизованной структуры любой сложности. Но об этом позже (быть может). А пока хочется остановиться на числах Рамсея. Для удобства перефразируем определение: 1. R(k, m) = R(m, k) 2. R(1, m) = 1 3. R(2, m) = m
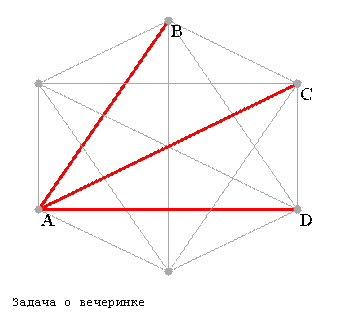
Остальные числа вычисляются индивидуально. Задача о вычислении R(3, 3) известна как "задача о вечеринке": среди любых 6 человек найдется либо 3 попарно знакомых, либо 3 попарно незнакомых. Другими словами R(3, 3) <= 6. Доказательство строится следующим образом (в терминах второго приведенного определения):
Вершина A соединена с пятью другими вершинами (красными и синими ребрами). Без ограничения общности можно считать, что она соединена красными ребрами по крайней мере с тремя вершинами - B, C, D. Далее, если одно из ребер BC, CD, BD красное (например BC), то имеем красный треугольник (ABC). Если же все они синие, то BCD - синий треугольник. Конец доказательства.
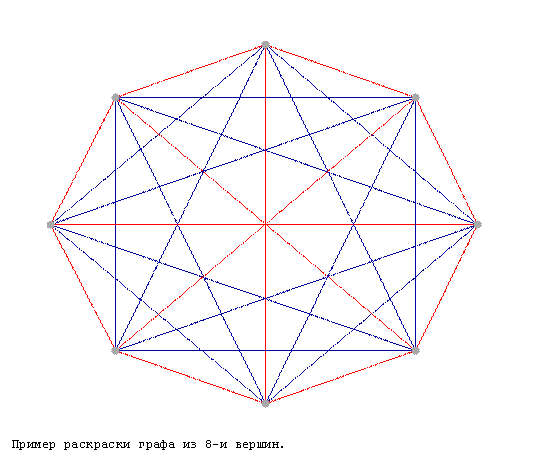
Осталось доказать, что полный граф из 9 вершин так раскрасить нельзя. Допустим, такая раскраска возможна. Будем рассуждать как в предыдущем доказательстве. Возьмем одну из вершин (A), с остальными вершинами она соединена 8 ребрами. Пусть k из них покрашены в красный цвет, а остальные 8-k - в синий. P.S. Данное доказательство пока не слишком сложное, но все же сложнее вычисления R(3, 3). Для больших параметров доказательства значительно усложняются. Дело в том, что не существует системного метода поиска чисел Рамсея (есть только грубые оценки), а с ростом параметров начинается очень обширное комбинаторное многообразие, не позволяющее найти решение даже компьютеру... P.P.S. Практического применения чисел Рамсея нет, но в процессе их поиска было разработано масса полезного инструментария как в теории графов, так и в смежных областях.
|