ВЕРОЯТНОСТНЫЙ ПОДХОД
Вероятность – числовая характеристика возможности появления какого-либо события в определённых условиях.
где m – число случаев (благоприятных), при появлении которых должно совершиться событие A, а n – общее количество случаев. Вероятность любого события заключена в отрезке от 0 до 1.
Зависимость между вероятностью появления события p и количеством информации I в сообщении о данном событии описывается модифицированной формулой Хартли:
 ,
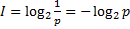т. е. чем меньше вероятность некоторого события, тем больше информации содержит сообщение об этом событии. (Здесь и ниже сообщение – некоторая последовательность чисел, с помощью которой закодирована информация.) Ещё одна формула для измерения количества информации – формула Шеннона:
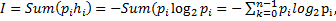
где I –КОЛИЧЕСТВО ИНФОРМАЦИИ, K – количество возможных событий, рi – вероятности отдельных событий Формулу Хартли можно рассматривать как частный случай формулы Шеннона:
Пример. Определить количество информации, которое содержится в сообщении о результате броска монеты. Решение. Возможно два равновероятных результата броска монеты: монета упала на «орла» или на «решку». Следовательно, вероятности появления сообщений «монета упала на орла» или «монета упала на решку» одинаковы и равны
Ответ: 1 бит.
|
,
.
. Вычислим количество информации в каждом сообщении о результате броска, используя формулу (3).:
